【排序算法】基数排序 agile Posted on Jul 13 2023 排序算法 >原创公众号:bigsai ## 前言 在排序算法中,大家可能对桶排序、计数排序、基数排序不太了解,不太清楚其算法的思想和流程,也可能看过会过但是很快就忘记了,但是不要紧,幸运的是你看到了本篇文章。本文将通俗易懂的给你讲解基数排序。 基数排序,是一种原理简单,但实现复杂的排序。很多人在学习基数排序的时候可能会遇到以下两种情况而浅尝辄止: - 一看原理,这么简单,懂了懂了(顺便溜了) - 再一看代码,这啥啥啥啊?这些的肯定有问题(不看溜了)  要想深入理解基数排序,必须搞懂基数排序各种形式(数字类型、等长字符类型、不等长字符)各自实现方法,了解其中的联系和区别,并且也要掌握空间优化的方法(非二维数组而仅用一维数组)。下面跟着我详细学习基数排序吧! ## 基数排序原理 首先百度百科看看基数排序的定义: > 基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,基数排序法的效率高于其它的稳定性排序法。 基数排序也称为卡片排序,简而言之,基数排序的原理就是多次利用计数排序(计数排序是一种特殊的桶排序),但是和前面的普通桶排序和计数排序有所区别的是,基数排序并不是将一个整体分配到一个桶中,而是将自身拆分成一个个组成的元素,每个元素分别顺序分配放入桶中、顺序收集,当从前往后或者从后往前每个位置都进行过这样顺序的分配、收集后,就获得了一个有序的数列。 在具体实现上如果从左往右那就是**最高位优先(Most Significant Digit first)法**,简称MSD法;如果从右往左那就是**最低位优先(Least Significant Digit first)法**,简称LSD法。但是不管从最高位开始还是从最低位开始要保证和相同位进行比较,你需要注意的是如果是int等数字类型需要保证从右往左(从低位到高位)保证对齐,如果是字符类型的话需要从左往右(从高位到低位)保证对齐。 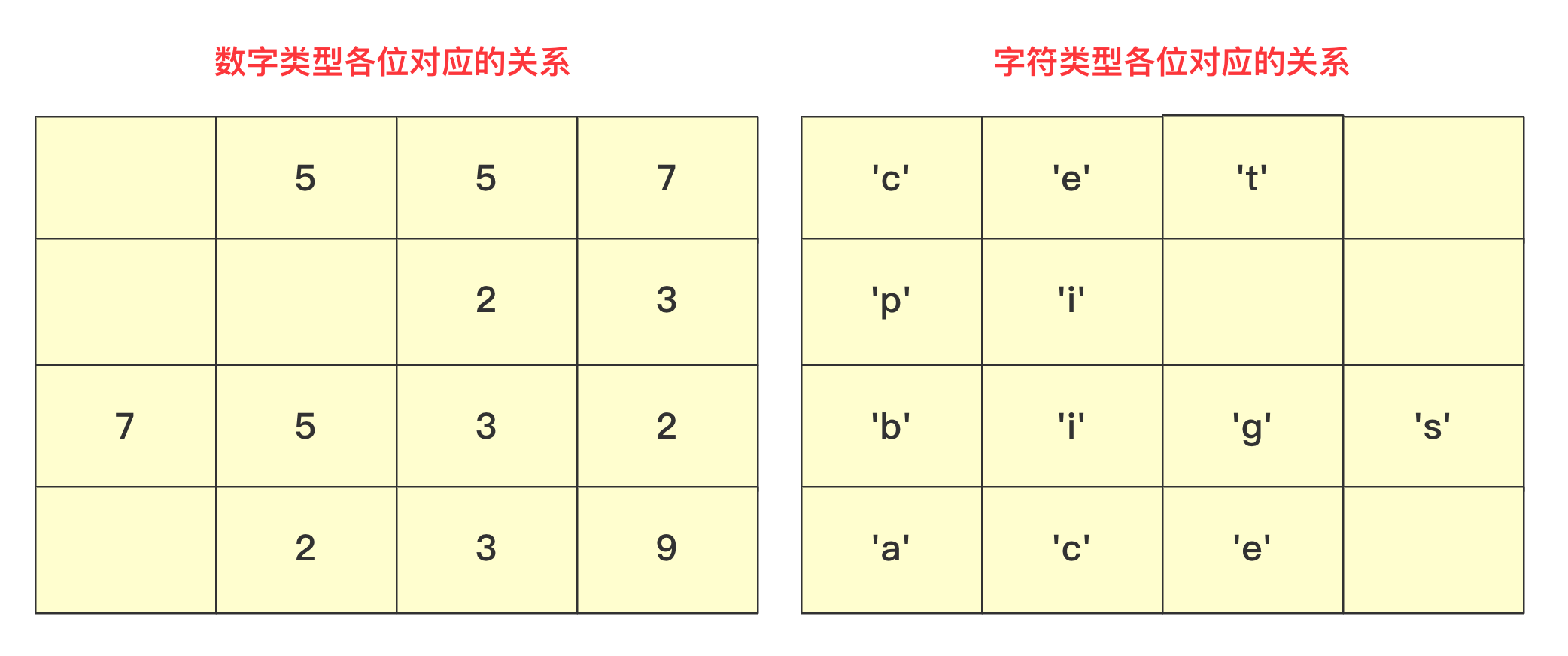 你可能会问为啥不直接将这个数或者这个数按照区间范围放到对应的桶中,一方面基数排序可能很多时候处理的是字符型的数据,不方便放入某个桶中,另一方面如果数字很大,不方便直接放入桶中。并且基数排序并不需要交换,也不需要比较,就是多次分配、收集得到结果。  所以遇到这种情况我们基数排序思想很简单,就拿 934,241,3366,4399这几个数字进行基数排序的一趟过程来看,第一次会根据各位进行分配、收集: 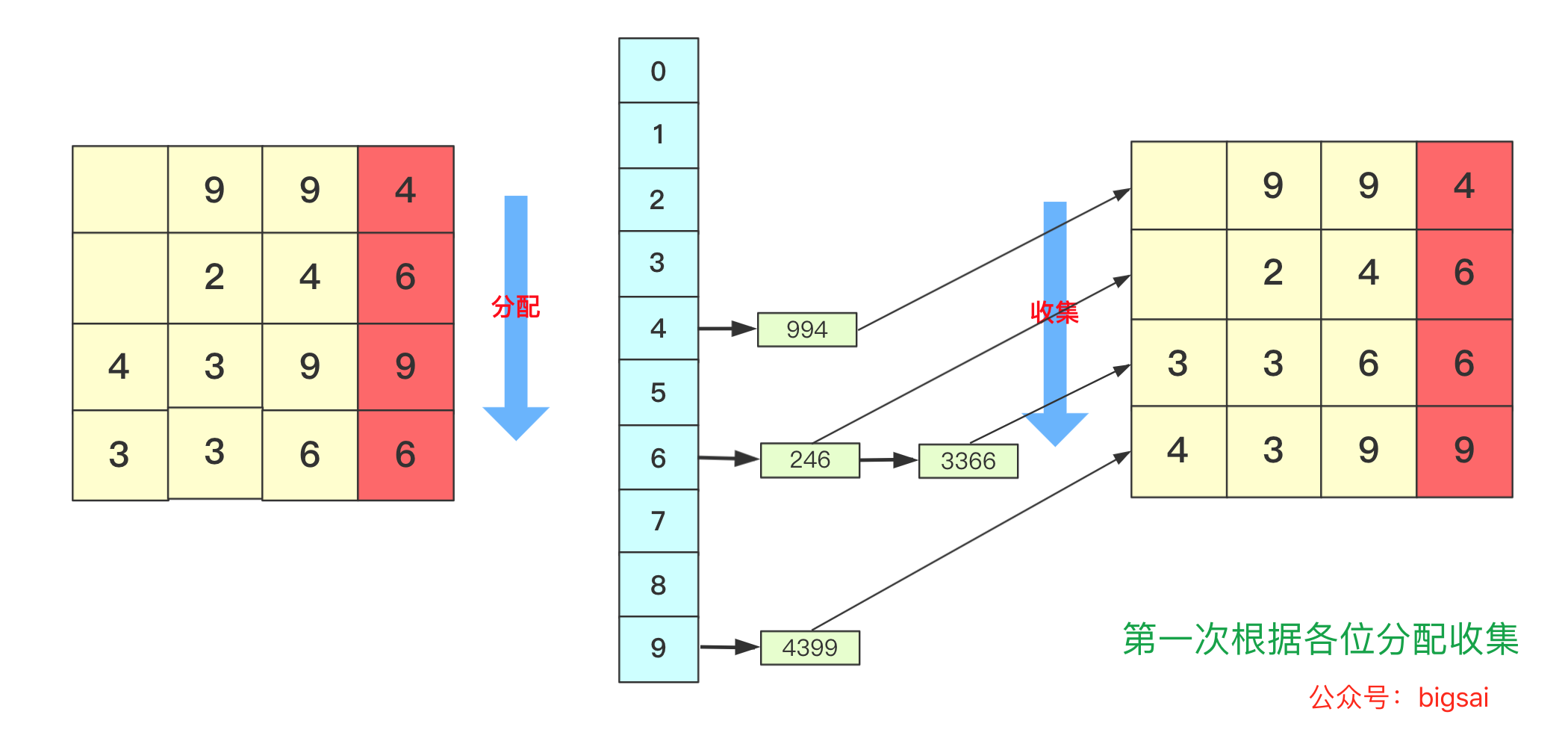 分配和收集都是有序的,第二次会根据十位进行分配、收集,此次是在第一次个位分配、收集基础上进行的,所以所有数字单看个位十位是有序的。 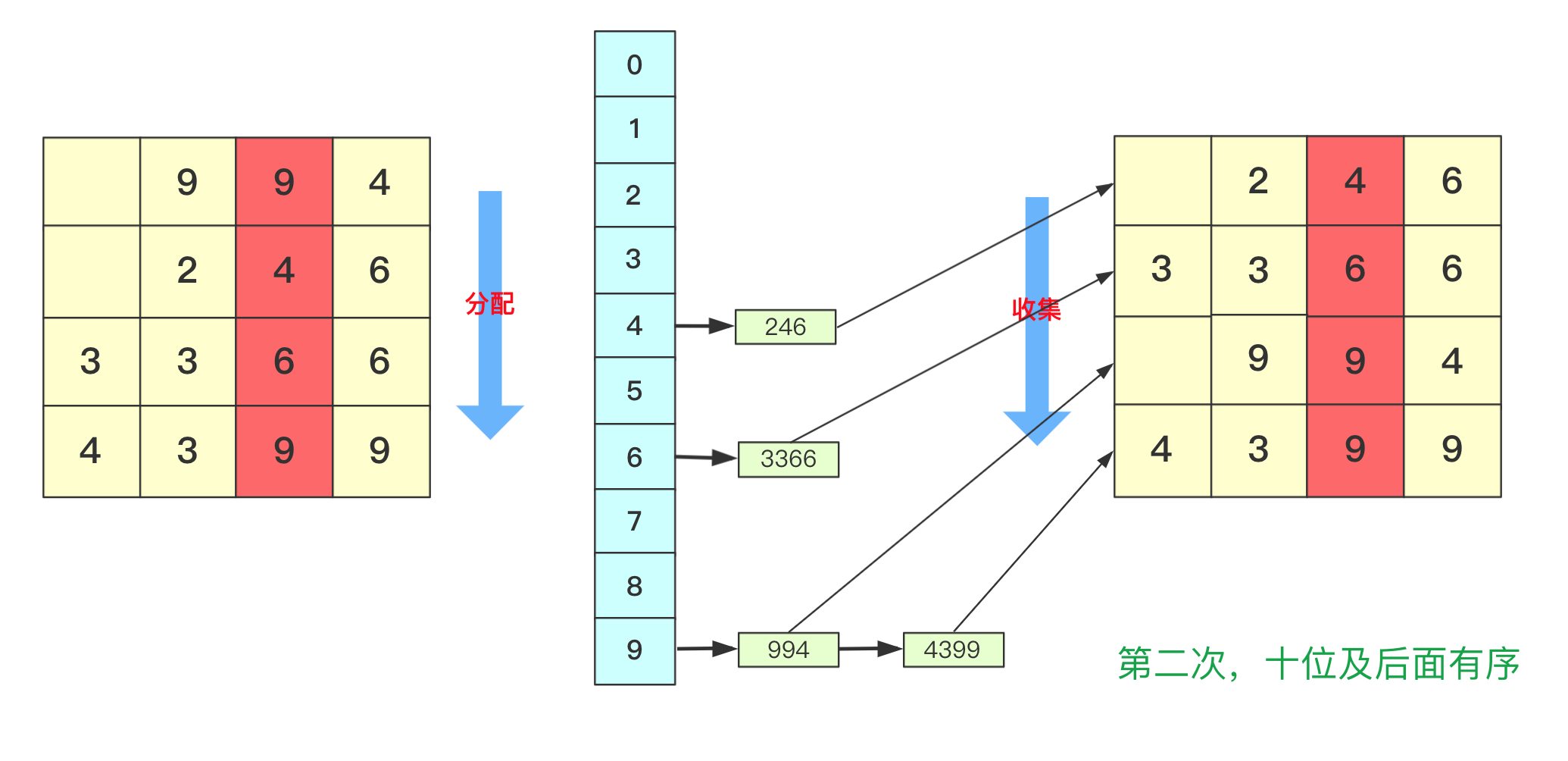 而第三次就是对百位进行分配收集,此次完成之后百位及其以下是有序的。 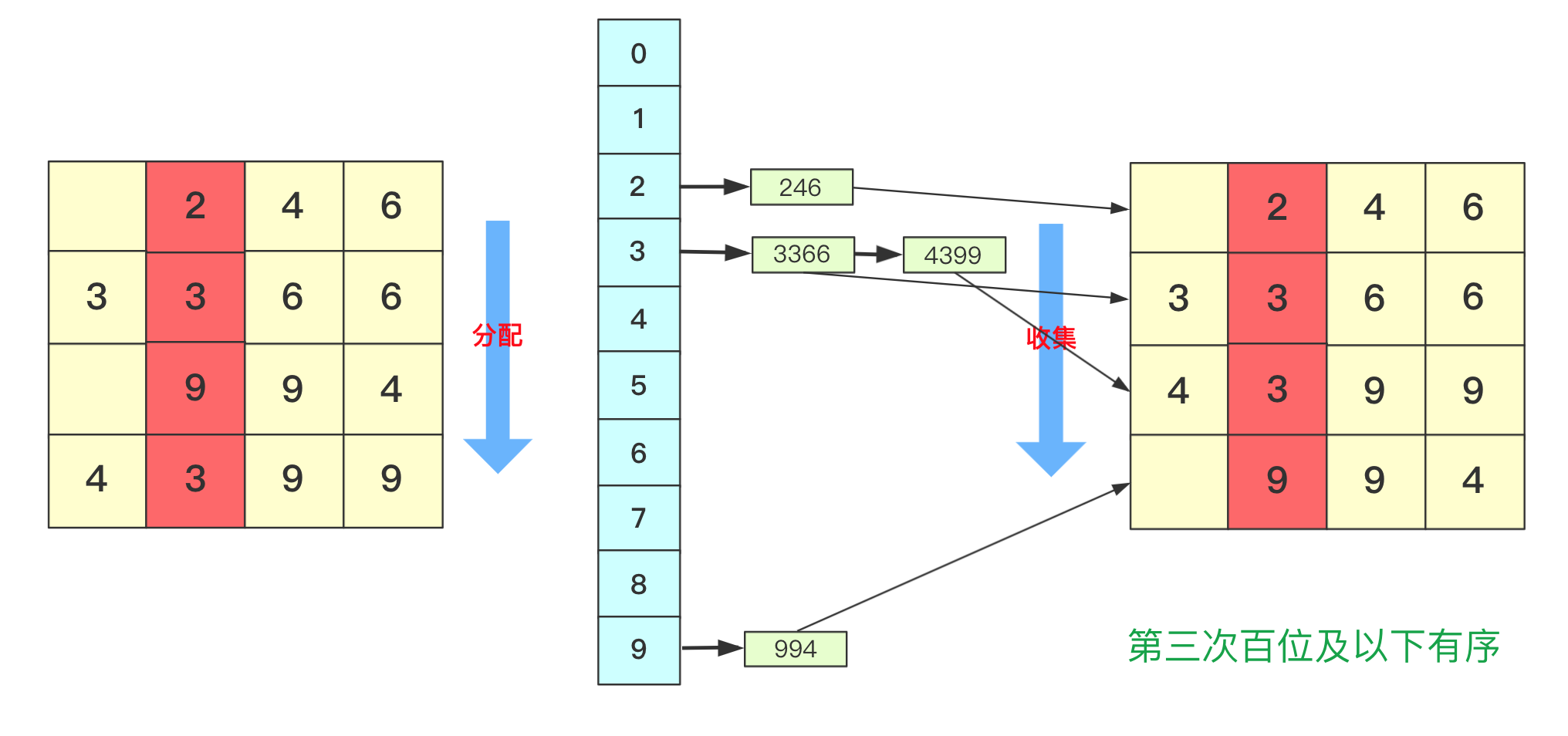 而最后一次的时候进行处理的时候,千位有的数字需要补零,这次完毕后后千位及以后都有序,即整个序列排序完成。 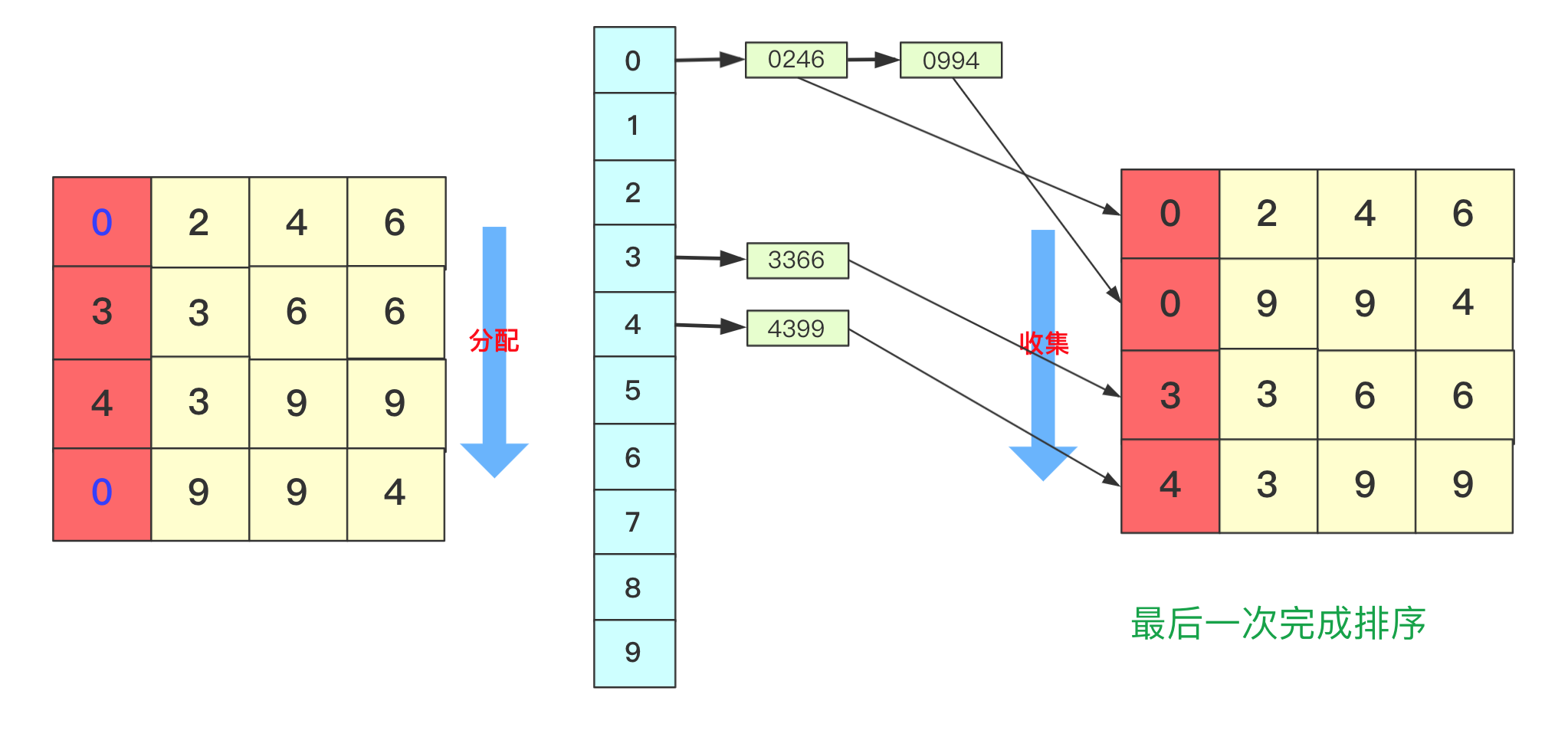 想必看到这里基数排序的思想你也已经懂了吧,但是虽然懂你不一定能够写出代码来,继续看看下面的分析和实现。 ## 数字类型基数排序 有很多时候也有很多时候对基数排序的讲解也是基于数字类型的,而数字类型这里就用int来实现,对于数字类型的基数排序你需要注意的有以下几点: - 无论是最高位优先法还是最低位优先法进行遍历需要保证数字各位、十位、百位等对齐,这里我使用最低位优先法从个位开始向上。 - 数字类型的基数排序需要十个桶(0-9),你可以使用二维数组,第一维度长度为10表示十个数字,第二个维度为数组长度,用来存储数字(因为最坏情况可能当前位数字一样)。但这样无疑太浪费内存空间了,你可以使用List或者Queue替代,这里就用List了。 - 具体实现要先找到最大值确定最高多少位,用来进行遍历时候确认。 - 收集的时候借助一个自增参数遍历收集。 - 每次收集完毕十个桶(bucket)需要清空待下次收集。 实现的代码为: ```java static void radixSort(int[] arr)//int 类型 从右往左 { List<Integer>bucket[]=new ArrayList[10]; for(int i=0;i<10;i++) { bucket[i]=new ArrayList<Integer>(); } //找到最大值 int max=0;//假设都是正数 for(int i=0;i<arr.length;i++) { if(arr[i]>max) max=arr[i]; } int divideNum=1;//1 10 100 100……用来求对应位的数字 while (max>0) {//max 和num 控制 for(int num:arr) { bucket[(num/divideNum)%10].add(num);//分配 将对应位置的数字放到对应bucket中 } divideNum*=10; max/=10; int idx=0; //收集 重新捡起数据 for(List<Integer>list:bucket) { for(int num:list) { arr[idx++]=num; } list.clear();//收集完需要清空留下次继续使用 } } } ``` ## 等长字符串基数排序 除了数字之外,等长字符串也是常常遇到的方式,其主要方法和数字类型差不多,这里也看不出策略上的不同。低位优先法或者高位优先法都可使用(这里依旧低位从右向左)。 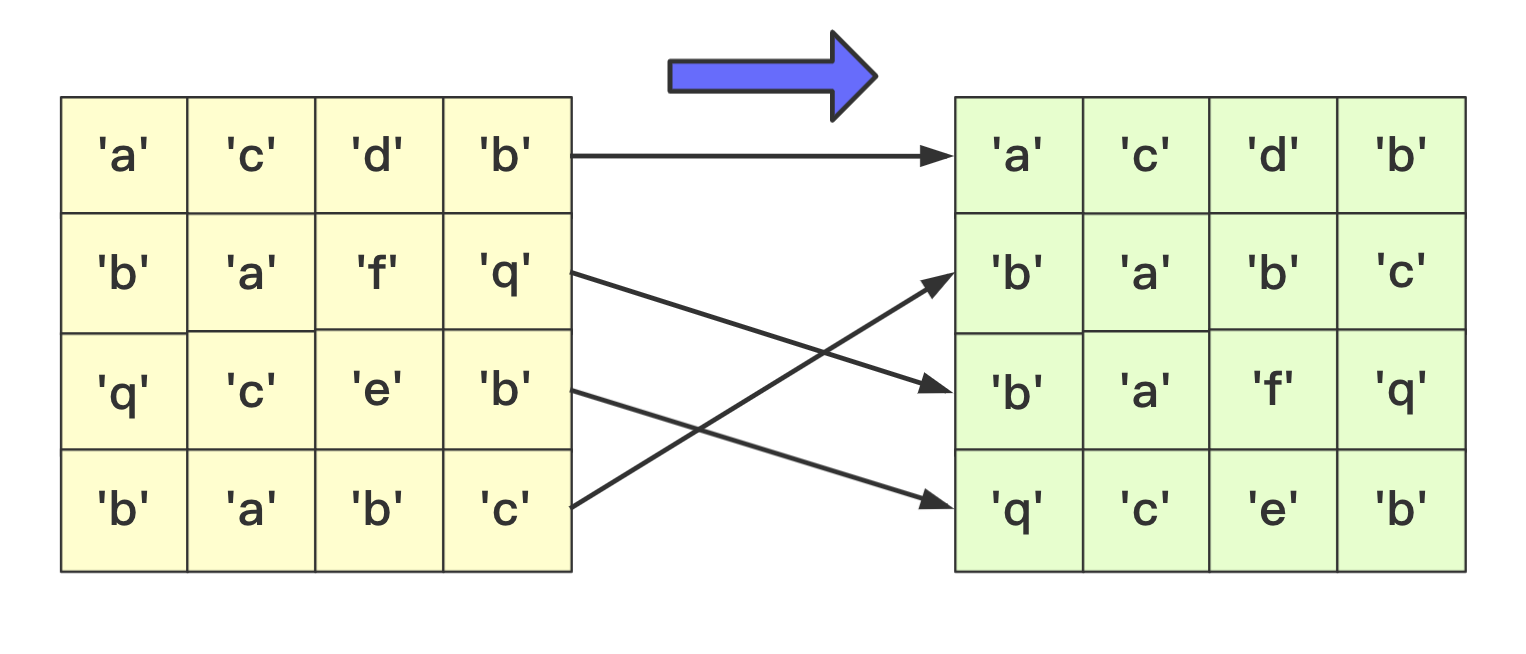 在实现细节方面,和前面的数字类型区别不是很大,但是因为字符串是等长的遍历更加方便容易。但需要额外注意的是: - 字符类型的桶bucket不是10个而是ASCII字符的个数(根据实际需要查看ASCII表)。其实就是利用char和int之间关系可以直接按照每个字符进行顺序存储。 具体实现代码为: ```java static void radixSort(String arr[],int len)//等长字符排序情况 长度为len { List<String>buckets[]=new ArrayList[128]; for(int i=0;i<128;i++) { buckets[i]=new ArrayList<String>(); } for(int i=len-1;i>=0;i--)//每一位上进行操作 { for(String str:arr) { buckets[str.charAt(i)].add(str);//分配 } int idx=0; for(List<String>list:buckets) { for(String str:list) { arr[idx++]=str;//收集 } list.clear();//收集完该bucket清空 } } } ``` ## 非等长字符串基数排序 等长的字符串进行基数排序时候很好遍历,那么非等长的时候该如何考虑呢?这种非等长不能像处理数字那样粗暴的计算当成0即可。字符串的大小是从前往后进行排列的(**和长度没关系**)。例如看下面字符串,“d”这个字符串即使很短但是在排序依然放在最后面。你知道该怎么处理吗? ``` "abigsai" "bigsai" "bigsaisix" "d" ``` 如果**高位优先**,前面一旦比较过各个字符的桶(bucket)就要固定下来,也就是在进行右面下一个字符分配、收集的时候要标记空间,即下次进行分配收集的前面是‘a’字符的一组,‘b’字符一组,并且不能越界,实现起来很麻烦这里就不详细讲解了有兴趣的可以自行研究一下。 而本篇实现的是**低位优先**。低位优先采用什么思路呢?很简单,跟我看图解。 第一步,先将字符按照长度进行分配到一个桶(bucket)中,声明一个`List<String>wordLen[maxlen+1]`;在遍历字符时候,以字符长度为下表index,将字符串顺序加入进去。其中maxlen为最长字符串长度,之所以要maxlen+1是因为需要使用maxlen下标(0-maxlen)。 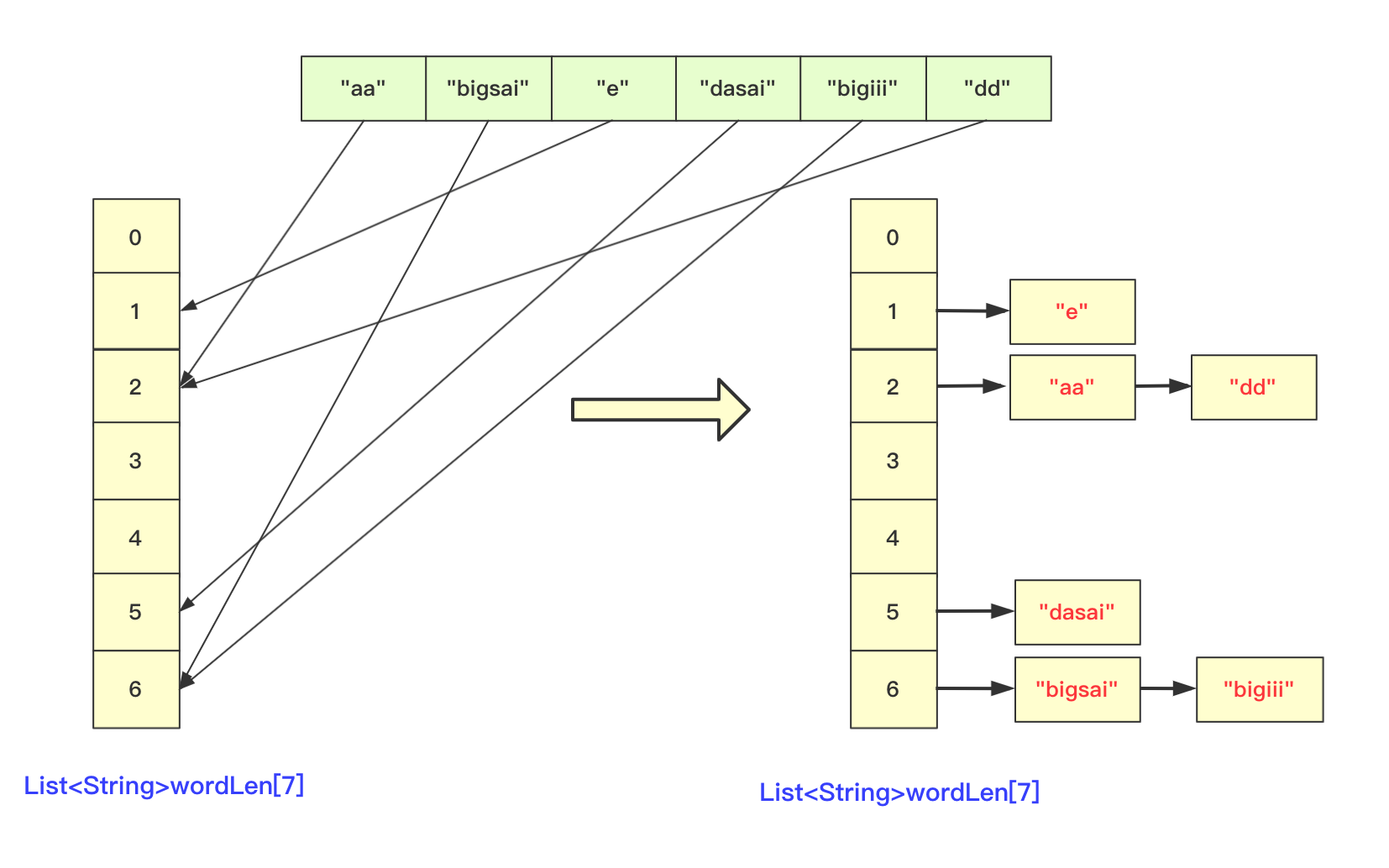 第二步,分配完成遍历收集到原数组中,这样原数组**在长度上相对有序**。  这样就可以进行基数排序啦,当然,在开始的时候并不是全部都进行分配收集,而是根据长度慢慢递减,长度可以到达6位分配、收集,长度到达5的分配、收集……长度为1的进行分配、收集。这样进行一遭就很完美的进行完基数排序,因为我们借助根据长度收集的桶可以很容易知道当前长度开始的index在哪里。 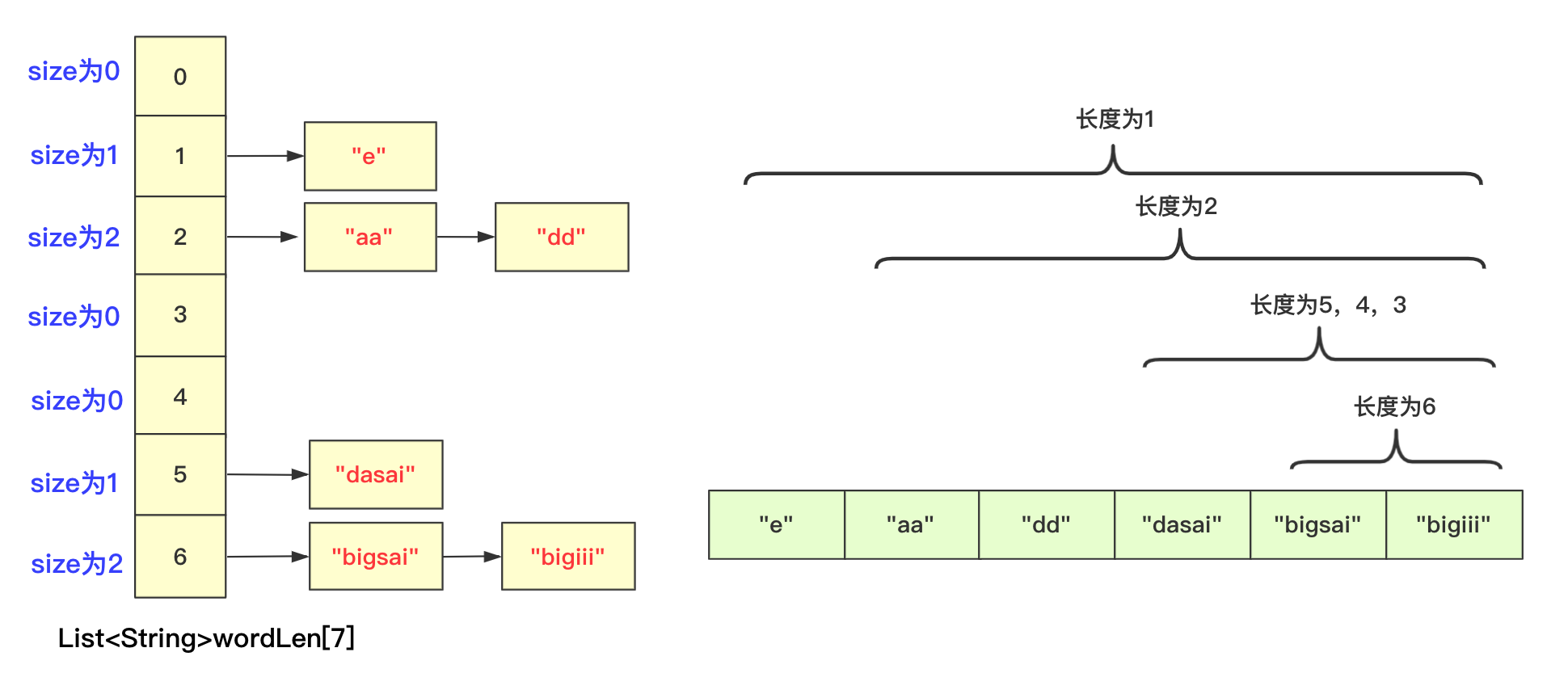 具体实现的代码为: ```java static void radixSort(String arr[])//字符不等长的情况进行排序 { //找到最长的那个 int maxlen=0; for(String team:arr) { if(team.length()>maxlen) maxlen=team.length(); } //一个对长度分 一个对具体字符分,先用长度来找到 List<String>wordLen[]=new ArrayList[maxlen+1];//用长度先统计各个长度的单词 List<String>bucket[]=new ArrayList[128];//根据字符来划分 for(int i=0;i<wordLen.length;i++) wordLen[i]=new ArrayList<String>(); for(int i=0;i<bucket.length;i++) bucket[i]=new ArrayList<String>(); //先根据长度来一下 for(String team:arr) { wordLen[team.length()].add(team); } int index=0;//先进行一次(按照长度分)的桶排序使得数组长度初步有序 for(List<String>list:wordLen) { for(String team:list) { arr[index++]=team; } } //然后 先进行长的 从后往前进行 int startIndex=arr.length; for(int len=maxlen;len>0;len--)//每次长度相同的要进行基数一次 { int preIndex=startIndex; startIndex-=wordLen[len].size(); for(int i=startIndex;i<arr.length;i++) { bucket[arr[i].charAt(len-1)].add(arr[i]);//利用字符桶重新装 } //重新收集 index=startIndex; for(List<String>list:bucket) { for(String str:list) { arr[index++]=str; } list.clear(); } } } ``` ## 空间优化(等长字符)基数排序 上面无论是等长还是不等长,使用的空间其实都是跟二维相关的,我们能不能使用一维的空间去解决这个问题呢?当然能啊。 在使用空间的整个思路是差不多的,但是这里为了让你能够理解我们在讲解的时候讲解**等长字符串的情况**。 先回忆刚刚讲的等长字符串,就是从个位进行遍历,在遍历的时候将数据放到对应的桶里面,然后在进行收集的时候放回原数组。 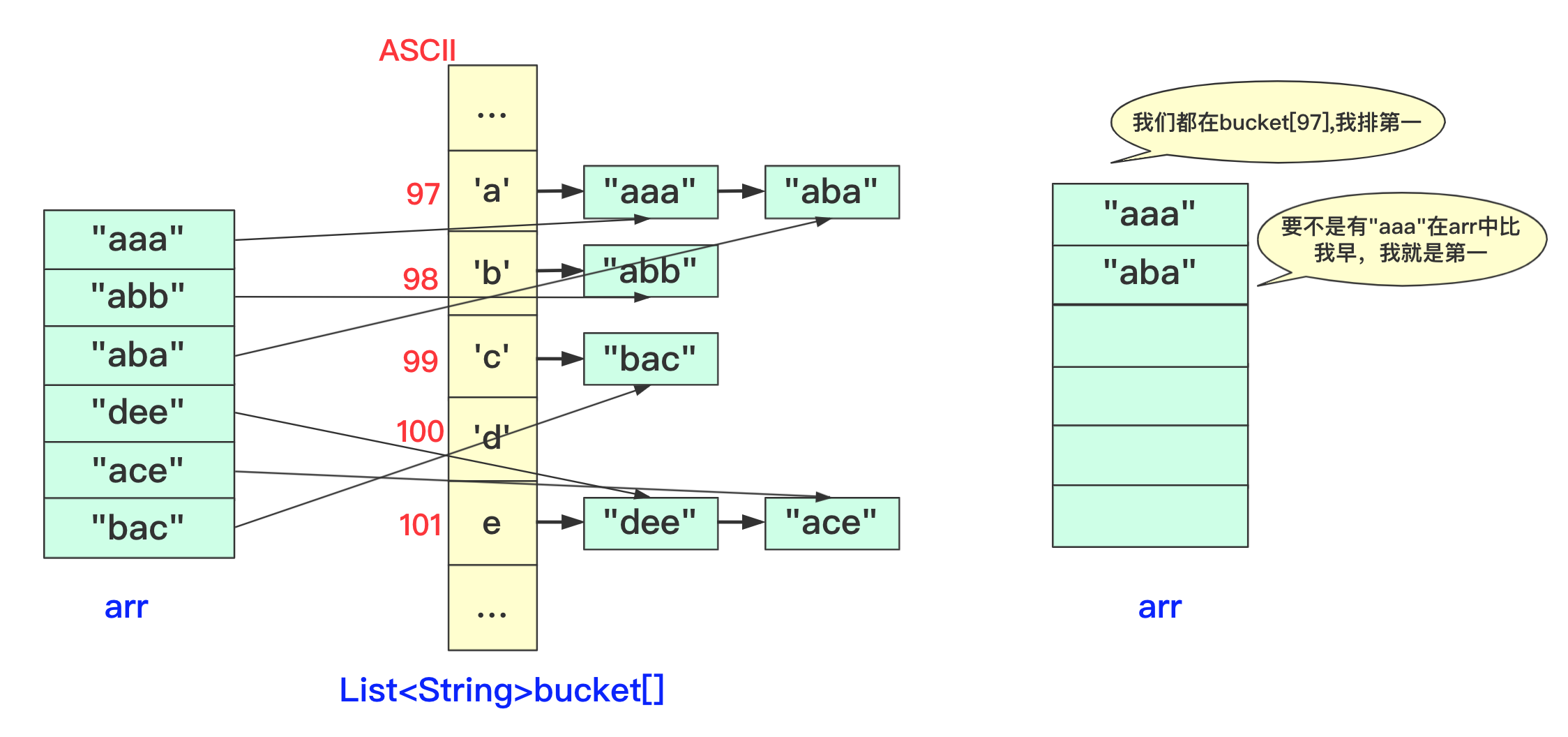 **你能否发现什么规律**? - 一个字符串收集的时候放的位置其实它**只需要知道它前面有多少个就可以确定**! - 并且**当前位置字符如果相同**那么就是根据arr中相对顺序来进行当前轮。 所以我们可以尝试来动态维护这个int bucket[]。第一次进行只记录次数,第二次进行叠加表示比当前位置+1编号小的元素的个数。 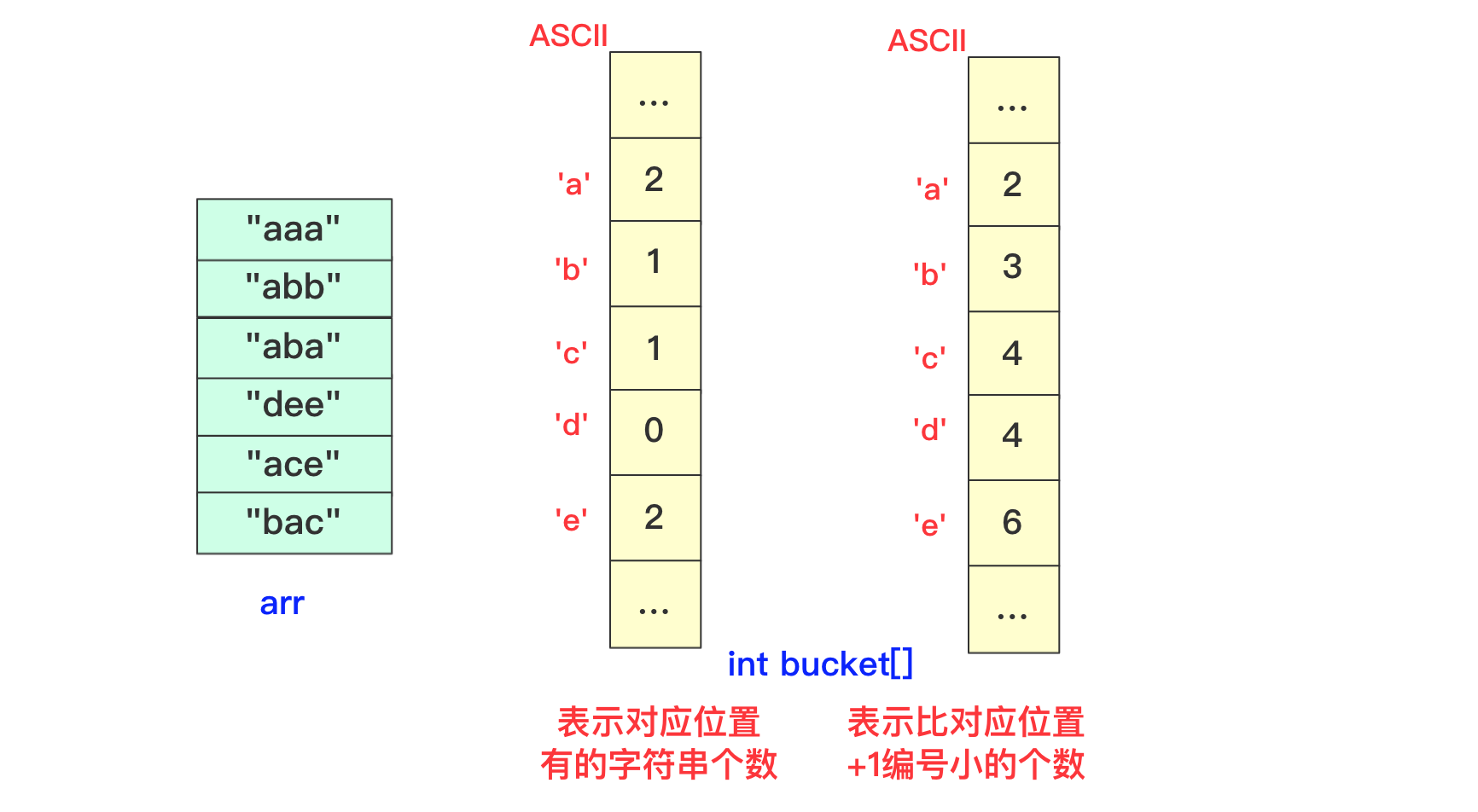 但是这样处理不太好知道比当前位置小的有多少,所以我们在分配的时候向下挪一位,这样bucket[i]就可以表示比当前位置小的元素的个数。 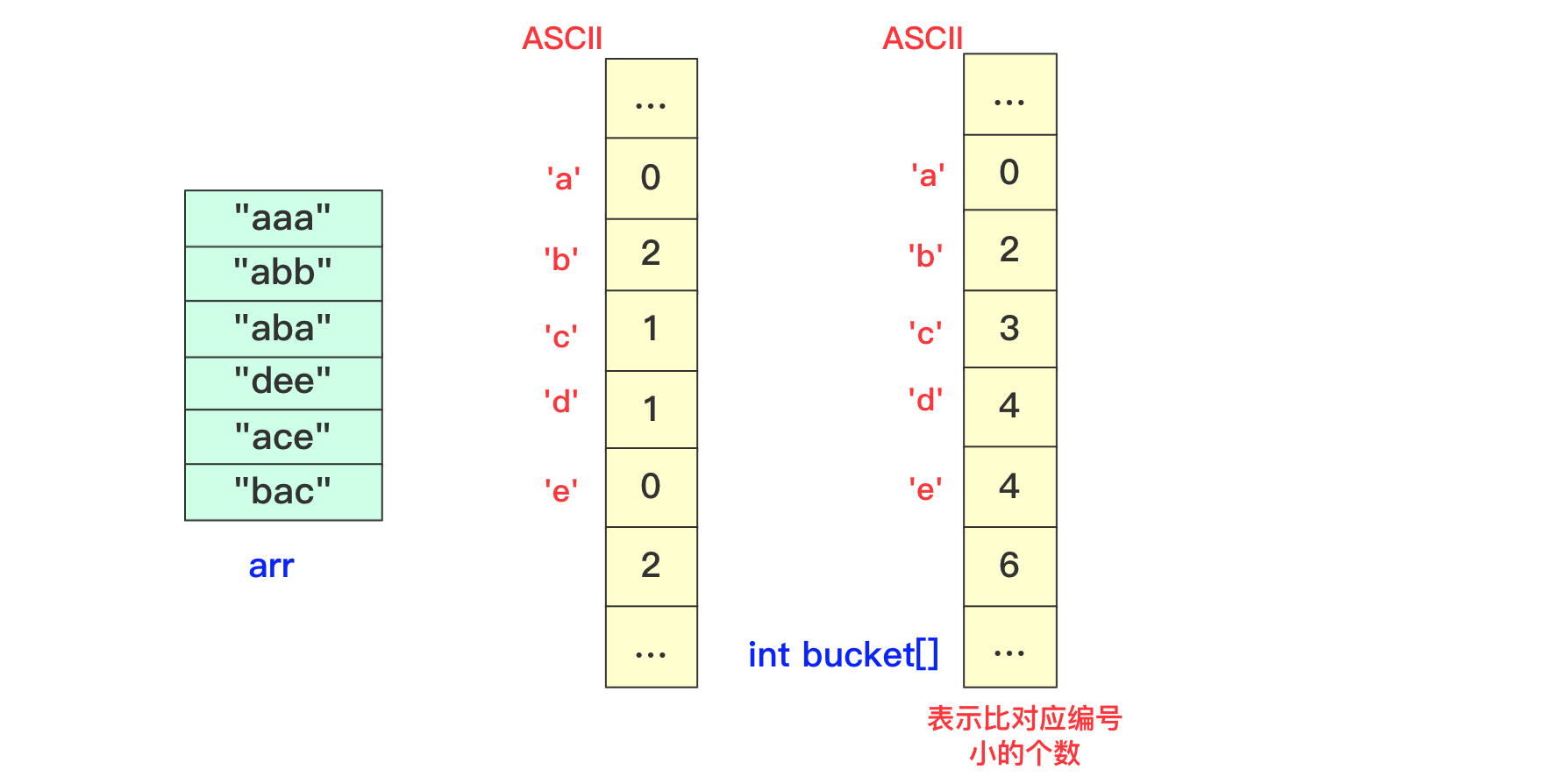 我们在进行收集的时候需要再次遍历arr,但我们需要一个临时数组String value[]储存结果(因为arr没遍历完后面不能使用),而进行遍历的规则就是:遍历arr时候对应字符串str,该位字符对应`bucket[str.charAt(i)]`桶中数字就是要放到arr中的编号(多少个比它小的就放到第多少位),放置之后要对bucket当前位自增(因为下一个这个位置字符串要把这个str考虑进去)。这样到最后即可完成排序。 第一趟遍历arr前两个字符串部分过程如下: 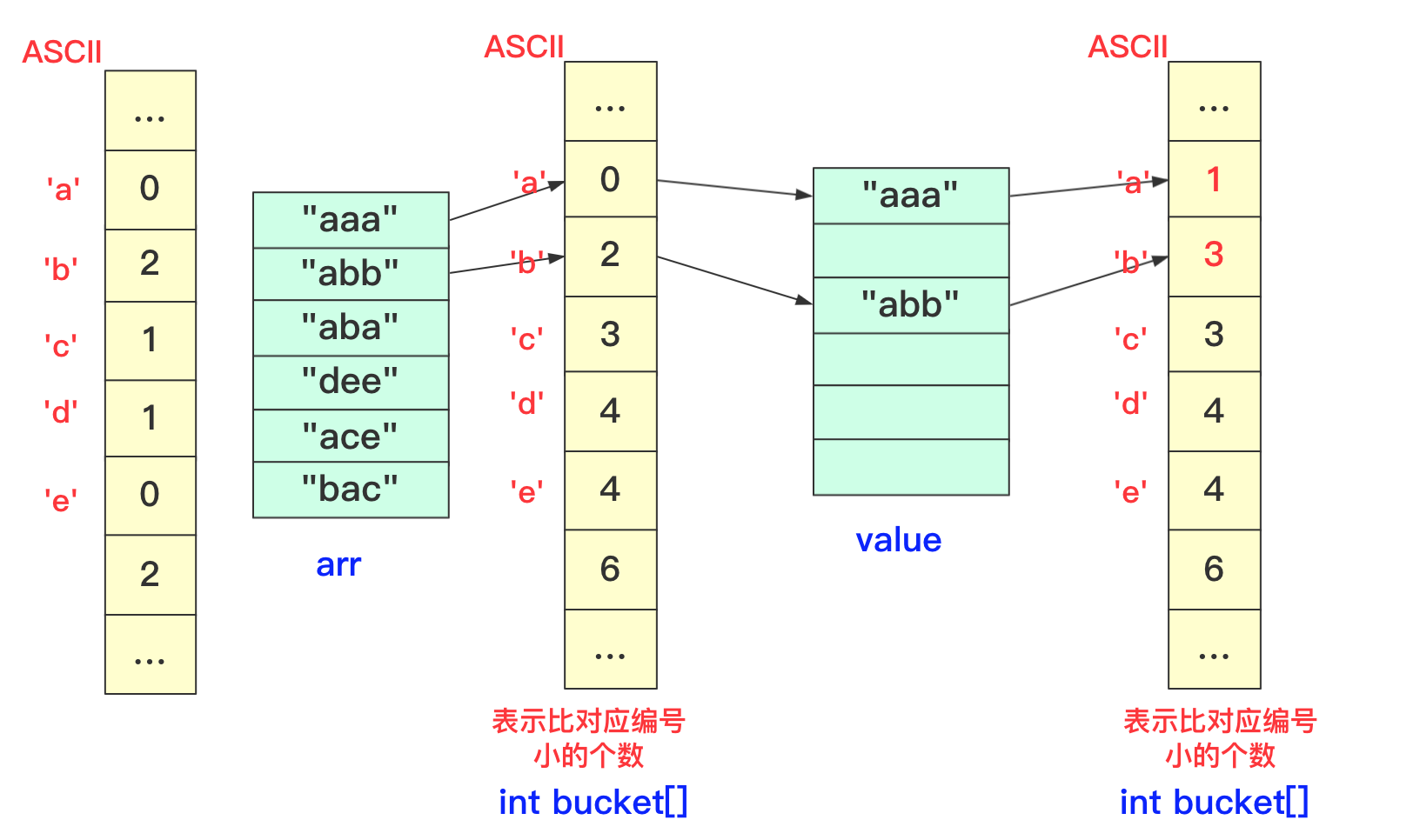 第一趟中间两个字符串处理情况: 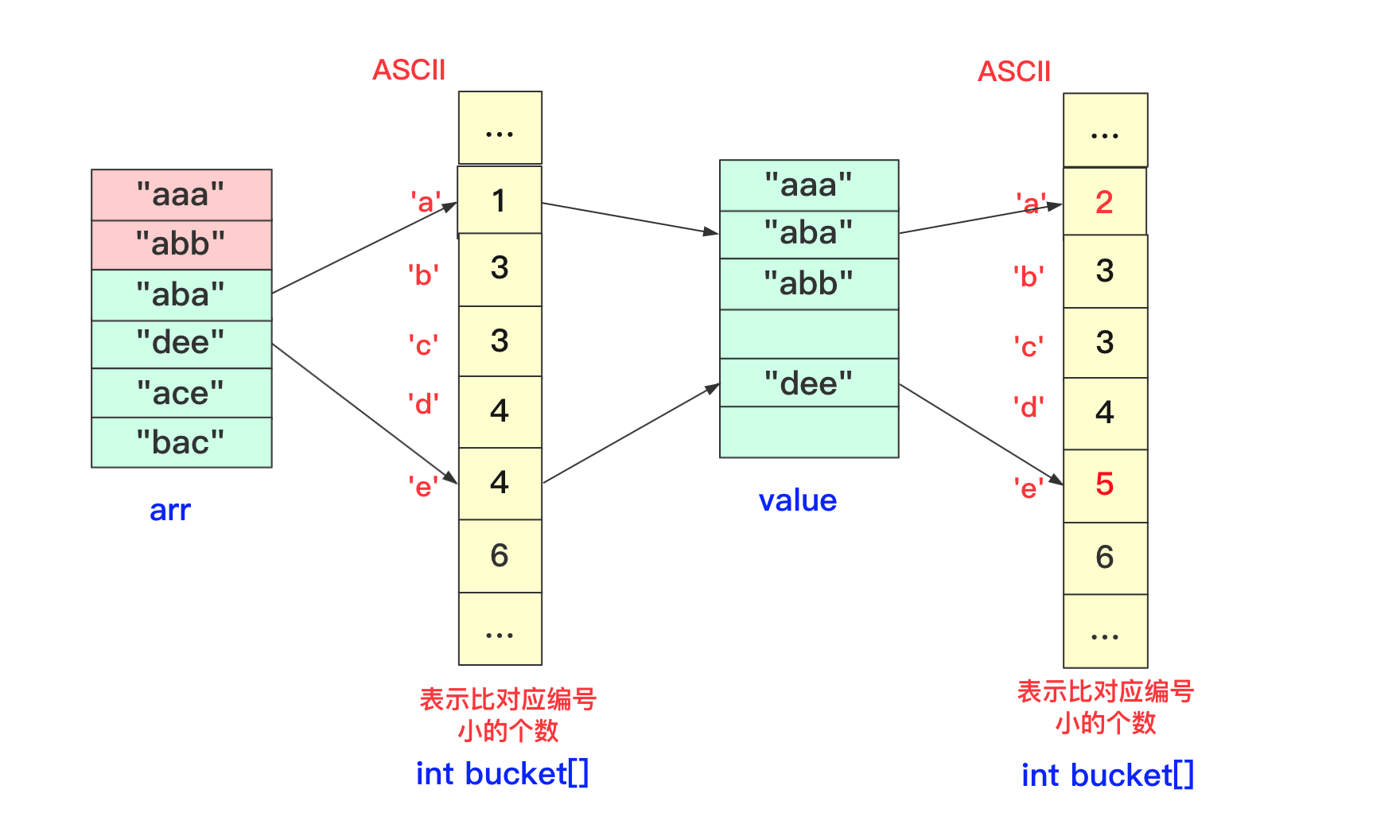 第一趟最后两个字符串处理情况: 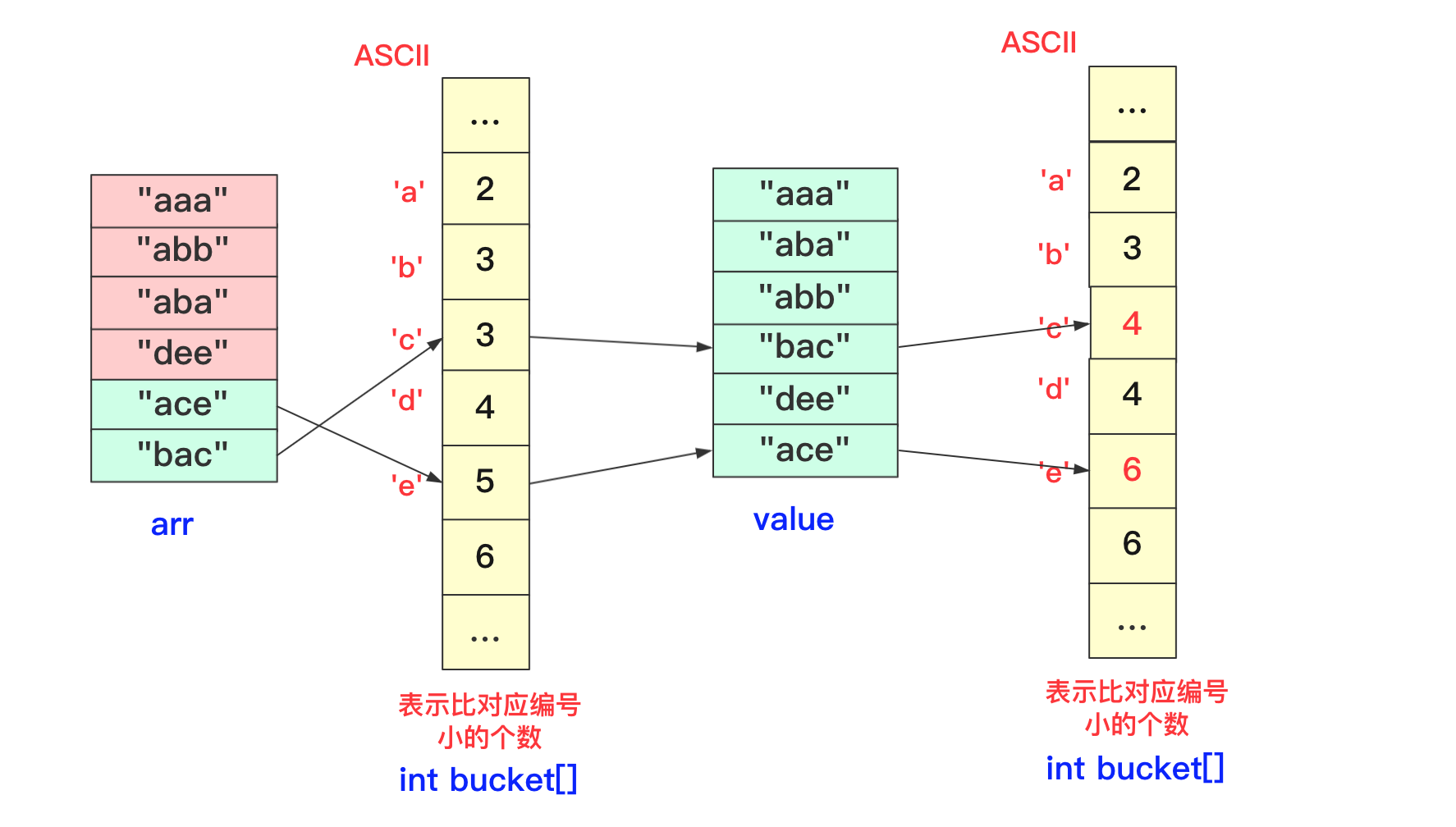 就这样即可完成一趟操作,一趟完成记得将value的值赋值到arr中,当然有方法使用指针引用可以避免交换数据带来的时间影响,但这里为了使大家更加简单理解就直接复制过去。这样完成若干次,整个基数排序即可完成。 具体实现的代码为: ```java static void radixSortByArr(String arr[],int len)//固定长度的使用数组进行优化 { int charLen=129;//多用一个 String value[]=new String[arr.length]; for(int index=len-1;index>=0;index--)//不同的位置 { int bucket[]=new int[charLen];//储存character的桶 for(int i=0;i<arr.length;i++)//分配 { bucket[(int)(arr[i].charAt(index)+1)]++; } for(int i=1;i<bucket.length;i++)//叠加 当前i位置表示比自己小的个数 { bucket[i]+=bucket[i-1]; } for(int i=0;i<arr.length;i++) { value[bucket[arr[i].charAt(index)]++]=arr[i];//中间的++因为当前位置填充了一个,下次再来同元素就要后移 } System.arraycopy(value,0,arr,0,arr.length);//copy数组 } } ``` 至于不定长的,思路也差不多,这里就留给你优秀的你自己去思考啦。 ## 结语 至于基数排序的算法分析,以定长的情况分析,假设有n数字(字符串),每个有k位,那么根据基数就要每一位都遍历就是K次,每次都是O(n)级别。所以差不多是O(n*k)级别,当然k远远小于n,可能有成千上万个数,但是每个数或者字符正常可没成千上万那么长。 本次基数排序就全讲完啦,那么多张图我想你也应该懂了。 最后我请你们两连事帮忙一下: 1. 点赞、关注一下支持, 您的肯定是我在平台创作的源源动力。 2. 微信搜索「**bigsai**」,关注我的公众号,不仅免费送你电子书,我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode,加我好友后期还会将总结的pdf免费送给你。  【排序算法】——图解双轴快排(建议收藏) 数据结构于算法—线性表