使用Raymarching和DistanceFunction绘制3D几何 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/367712078) 在上一篇文章中,简单的介绍了使用距离函数绘制二维图形。 [王江荣:Shader 中使用距离函数(Distance Function)绘制二维图形](https://zhuanlan.zhihu.com/p/365440831) 现在我们来看看**怎么使用距离函数来绘制出 3D 几何**的效果。 在理解了 2D 距离函数的意义后,想要写一些简单的 3D 几何的距离函数本身并不困难,基本把输入的 vec2 改成 vec3,然后判断下 z 轴的值即可,例如球和立方体,我们很容易就可以写出来。 **球的距离函数** ``` float sdSphere( vec3 p, float s ) { return length(p)-s; } ``` **立方体的距离函数** ``` float sdBox( vec3 p, vec3 b ) { vec3 q = abs(p) - b; return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0); } ``` 其他基础几何的距离函数我们可以参考大佬的文章: [fractals, computer graphics, mathematics, shaders, demoscene and more](https://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm) 二维变三维 ----- 我们来对比下圆和球的距离函数的区别,如下: ``` //球 float sdSphere( vec3 p, float s ) { return length(p)-s; } //圆 float sdCircle( vec2 p, float r ) { return length(p) - r; } ``` 区别在哪?区别在所谓的空间中任意点,从一个 vec2 的二维点变成了 vec3 的三维点。可是我们知道屏幕中每个像素点都是一个二维的坐标 (u,v),现在要我们输入三维的点,这怎么搞?这个问题个人觉得是实现三维场景最重要的一点。 既然原本是二维的 (u,v),我们想要变成三维的自然是要**增加一个维度**。第一时间能想到的最简单的方法自然是把 (u,v) 写成(u,v,w),然后给 z 定义一个取值范围,例如 0-2,取 / 采样 100 次。这样的话原本我们屏幕像素假设有 1000 个,我们就可以得到 1000*100 个空间中的点,然后用这些点带入三维的距离函数。代码如下: ``` void mainImage( out vec4 fragColor, in vec2 fragCoord ) { vec2 p = (2.0*fragCoord-iResolution.xy)/iResolution.y; for(int i = 0; i < 100; i++) { vec3 p3 = vec3(p, i * 0.02); float d = sdBox(p3, vec3(0.25)); ... } ... } ``` 什么感觉?这是不是就像**正交投影**,每个像素有一条垂直于屏幕的射线往 z 轴正方向射。但是若想实现 3D 的效果,肯定是不能用正交投影的,而应该使用**透视投影**。 注:opengl 中使用的是**左手坐标系**,也就是说我们的 z 轴的正方向是朝向屏幕内的,而非朝向屏幕前的程序猿。 Raymarching ----------- 想要实现透视投影的效果,Raymarching 可以帮到我们。首先我们先发挥**空间想象力**,想象如下一个场景:空间中有个摄像机,看向我们的屏幕,而我们屏幕后面就是我们要显示的几何(如下图)。 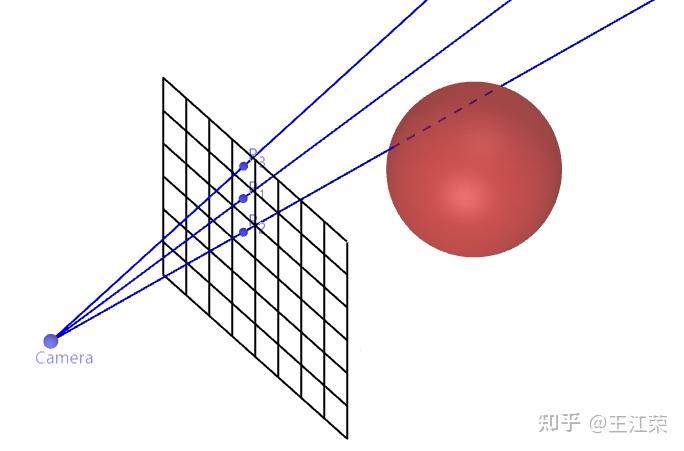 那么 raymarching 是啥子呢?我们把这个单词拆开来看: 1. ray,即射线,既然是射线,那么就需要一个起点和一个方向。在上面的场景中,射线的起点即为我们的 camera,而方向则是每个像素的中心点。 2. marching,前进、步进,也就是说我们的 ray 是根据某个步长一点点前进的,如果射线打到物体表面则停止,否则继续前进直到达到最大值。 **那么所谓的 raymarching,通俗来说,就是我们会在从摄像机往每个像素的中心点发射一条射线,该射线按照一定的步长前进。如果该射线打到了一个物体的表面上,那么射线就停止前进,同时对应像素应该显示该物体的信息。此外还可以得到一个交点,我们可以利用它来计算阴影等。** 那么我们就可以定义一个摄像机的位置 vec3 orign,然后根据每个像素的坐标定义一个方向 vec3 direction,那么当射线前进到一定的长度 float len 后,射线末尾的点坐标自然就是: ``` vec3 p = orign + direction * len ``` 这个 p 就是空间中的一个点了,至于射线是否打到了物体表面,我们不就可以**把 p 带入到距离函数当中,若得到的值为 0,即打到了物体表面**。打到物体表面,也就说明我们的像素应该显示这个物体。 那么我们就可以写出和射线相关的函数了: ``` // 输入射线的起点和方向,返回射线的长度 float raycast(in vec3 orign, in vec3 direction) { float lenMin = 0.0; float lenMax = 20.0; float len = lenMin; for(int i = 0; i < 70 && len < lenMax; i++) { // 带入距离函数 float d = map(orign + direction * len); // 射线越长,精度越低 if(abs(d) < (0.001*len)) return len; // 步长 len += d; } return -1.; } ``` 其中 len+=d 的含义为:t 是此时射线的长度,d 是此时射线尾端到物体表面的最短距离,也就是说 len+=d 要么正好使射线到达物体表面,要么依旧还没到物体表面。使用这个方法就不需要利用定死的步长,一点点的加长射线了。当然了,这个步长方法也有它的缺点,我们后面会讲到。 其中 map 函数我们后面再绘制场景的部分介绍。 定义相机相关参数 -------- 接着我们可以在 mainImage 方法中定义一下摄像机的位置,以及每个像素对应的射线方向,焦距,以及射线起点,如下: ``` void mainImage( out vec4 fragColor, in vec2 fragCoord ) { vec2 p = (2.0*fragCoord-iResolution.xy)/iResolution.y; vec3 camera = vec3(0.0, 1.0, -3);//相机位置 const float fl = 3.0;// focal length 焦距 vec3 direction = normalize(vec3(p, fl));//射线方向 vec3 orign = vec3(camera.x + p.x, camera.y + p.y, camera.z + fl); //射线起点 float len = raycast(orign, direction); //发射 } ``` 效果大致如下:  这里我们每个射线的起点并不是相机,而是把每个像素作为起点,因为如果物体在相机和像素之间,我们不应该看到它。 我们也可以让相机绕某个轴旋转,或者低头抬头看,因为当我们相机转动的时候,屏幕位置理论上也是跟着一起变化,因此我们需要对 direction 做一个**矩阵的转换**,这里就不过多介绍了。 还有我们需要注意一下**单位**,**单位长度 1 代表着屏幕高度的一半(因为 uv 的变换操作)**,上面我们 camera 的 y 为 1,也就是说如果我们有个 y=0 的平面的话,那个屏幕最下面的一排像素 (u, -1) 正好在这个平面上。 这里满绕的,大家可以多想想,理清楚。 绘制场景 ---- 摄影师搞定,接着轮到我们的主角登场。我们的主角自然就是前面说的几何图形,我们用距离函数来绘制它们。如果要绘制多个几何,我们只需要使用 opUnion 方法即可(在 2D 中介绍过了)。 这里我们把整个绘制过程放在一个 map 函数里,如下: ``` float sdPlane(vec3 p) { return p.y; } float opUnion(float d1, float d2) { return min(d1,d2); } //输入空间中的点(射线上的点),返回最短距离 float map(in vec3 pos) { float d = 1e10; d = opUnion(d, sdPlane(pos));//画一个y=0的平面 d = opUnion(d, sdSphere(pos+vec3(-0.3,-0.6,-2.), 0.4));//画一个球 d = opUnion(d, sdBox(pos+vec3(0.9,-0.5,-2.), vec3(0.3)));//画一个正方体 return d; } ``` 这样我们只需要把射线上的点带入到 map 函数里,就可以判断出该点是否在物体表面上了。 这里,我们整个过程基本就已经完成了,最后我们只需要把 raycast 返回长度大于等于 0 的像素设置为白色(射到了在物体表面上),等于 - 1 的像素设为其他颜色(没射到物体)即可。 那么我们可以得到下面这样的结果: 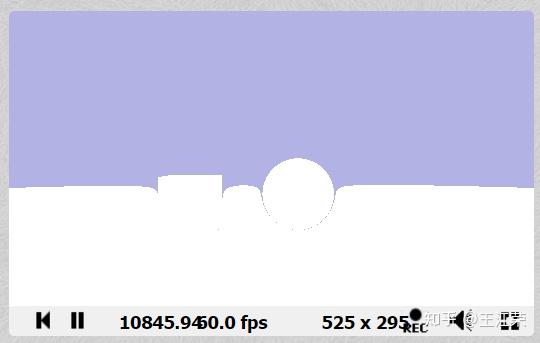 首先最明显的一个问题,我们的平面在和其他几何相加的地方,怎么扭曲了?这个问题其实就是之前步长的设置所导致的。 例如我们有个射线是图中的小黑点(如下图),那么这个射线自然是往小黑点方向射的。  那么它会做如下循环: 1. i=0 ,len=0,假设到球的最短距离为 2。 2. i=1,len=2,此时我们射线屁股已经很接近球了,假设最短距离为 0.2。 3. i=2,len=2.2,此时射线更接近球了,可能就离球 0.002。 4. i=3,len=2.202,此时射线还是离球很近,假设 0.003 到这,我们就会发现,这种情况下当 i 递增的时候,我们每次步长都会非常的小,当 i=70 结束的时候,可能射线的长度都不足以射到平面上,导致认为这根射线没有射到物体表面。 我们可以做些优化,例如增加 i 的取值范围等。但是这里,我们介绍另外一种绘制平面的方式。我们先来看个示意图,如下:  如果我们要显示一个低于相机的水平平面,那么只有图中蓝色的射线可能打到这个平面,红色的射线永远不可能打到它。 那么我们怎么求蓝色射线的长度?我们知道射线的起点为 orign,方向为 direction,终点肯定在平面上,即 y=0。那么我们就可以得到:orign+direction*len=(?,0,?),我们只看 y 这一项,不就可以得到: > len=(0-orign.y)/direction.y 蓝色的射线 len>0,红色的射线 len<0,也就是说,我们可以直接求得射线打到 y=0 的平面上的距离,既然能直接求出来,那么也就不需要去 marching 慢慢加了。同时因为我们不显示平面下的物体,因此也可以对 marching 时,最大射线长度进行更进一步的限制。 修改后的代码如下: ``` // 输入射线的起点和方向 float raycast(in vec3 orign, in vec3 direction) { float len2return = -1.; float lenMin = 0.0; float lenMax = 20.0; //绘制平面 float len2plane = (0.0-orign.y)/direction.y; if(len2plane > 0.0) { lenMax = min(lenMax, len2plane); len2return = len2plane; } float len = lenMin; for(int i = 0; i < 70 && len < lenMax; i++) { // 带入距离函数 float d = map(orign + direction * len); // 射线越长,精度越低 if(abs(d) < (0.001*len)) return len; // 步长 len += d; } return len2return; } ``` 我们就可以得到下面这样的效果:  可以发现不仅交界处的扭曲没有了,平面的远处也都一览无余,因为不需要用 marching 就可以判断出会不会打到平面上了。 几何自定义参数 ------- 此时如果难搞的美术说,我想要球是红色的,小方块是蓝色的,那怎么搞?前面我们只能通过距离函数来知道点是否在物体表面上,至于在什么物体,我们压根不晓得。 因此针对上面这样的需求,我们就要想办法来增加参数来区分它们。原理很简单,我就直接贴代码了,之前的 map 函数只返回一个最短距离,我们给它修改修改: ``` vec2 opUnion(vec2 d1, vec2 d2) { return d1.x < d2.x ? d1 : d2; } vec2 map(in vec3 pos) { vec2 res = vec2(1e10, 0); res = opUnion(res, vec2(sdSphere(pos+vec3(-0.3,-0.9,-2.), 0.4), 2)); res = opUnion(res, vec2(sdBox(pos+vec3(0.9,-0.8,-2.), vec3(0.3)), 3)); return res; } ``` 如代码,我们根据不同的距离函数,给它带一个新的值,当然我们也可以带更多的值。其他相关代码也需要修改,这里就不贴代码了,后续直接看完整的代码即可。 我们就可以得到如下效果: 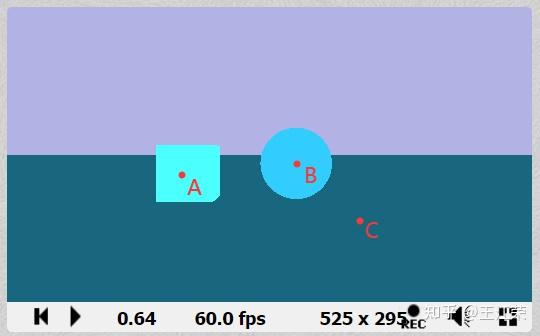 我们用这几个点来理解下上面代码的妙处,例如: * map 函数带入 A 点,那么在圆的距离函数里可能得到 (0.5, 2),然后在方块的距离函数里会得到 (0, 3),通过 opUnion 方法,最终会得到 (0, 3)。 * map 函数带入 B 点,那么在圆的距离函数里可能得到 (0, 2),然后在方块的距离函数里会得到 (0.5, 3),通过 opUnion 方法,最终会得到 (0, 2)。 发现了吧,当我们最终得到表面上的点时,返回值 vec2 的第二个值永远是我们点所在的几何有关,因此我们就可以通过这个值进行一些区分的逻辑。 着色 -- 摄影师,主角都搞定了,我们还需要一个灯光师。 想要更有 3D 的效果,着色是必不可少的,我们就来简单的着色一下。 [王江荣:着色与 Blinn-Phong 反射模型](https://zhuanlan.zhihu.com/p/364086530/edit) 在着色之前,我们先来看看一些着色需要的值怎么求得。 ### 计算表面上点的坐标 有了射线的起点,方向和长度,我们很容易就可以求出着色点的坐标。 ``` vec3 p = orign + direction * res.x; ``` ### 计算球面上点的法线 要着色,着色点的法线是必不可少的。前面我们已经求出球面上任意点的坐标,那么该点的法线应该怎么求呢?并且我们现在场景中并不只是一个几何物体,而是有多个,不同几何物体上的法线求法理论上也不一样。 那么有没有什么统一的好方法呢?有,我们可以利用**梯度**来求法向量。 可以参考下面这篇文章: [undefined](https://iquilezles.org/www/articles/normalsSDF/normalsSDF.htm) 方法如下: ``` vec3 CalNormal(vec3 p) { vec2 e = vec2(1.0,-1.0)*0.5773*0.0005; return normalize(e.xyy*map(p + e.xyy).x + e.yyx*map(p + e.yyx).x + e.yxy*map(p + e.yxy).x + e.xxx*map(p + e.xxx).x ); } ``` ### 模拟点光源 接着我们需要在场景中模拟一个光,当然了,这个光它并不会发光,仅仅只是一个位置信息。通过光源的位置,我们就可以计算出着色点到光源的向量,然后用该向量来计算漫反射镜面反射。代码如下: ``` vec3 sum = vec3(-2.0,2.0,-2.0); vec3 p2sum = normalize(sum-p); ``` ### 漫反射 上面都定义好后,我们就可以通过漫反射的公式来实现着色了: >  代码如下: ``` col = vec3(1); vec3 kd = vec3(0.9); col = kd * max(0.0, dot(p2sum, normal)); ``` 注:为了方便,这边省略了光能量与光到着色点距离这一项,高光计算也是如此。 ### 高光 由于高光和观测方向也有关,前面我们已经定义了 Camera 在原点,那么我们就可以根据着色点的位置,计算出观测的方向。 ``` vec3 p2camera = normalize(orign-p); ``` 这里我们需要计算一个半程向量,其公式为: >  所以代码如下: ``` vec3 cs = p2camera + p2sum; vec3 h = cs/dot(cs,cs); ``` 这样我们就可以利用高光的公式来添加高光效果了,公式如下: >  代码为: ``` vec3 ks = vec3(1.0); col += ks * pow(max(0.0, dot(h, normal)), 3.0); ``` 环境光 --- 环境光就很简单了,啥都不需要考虑,加个颜色即可: ``` if(res.y == 1.) col += vec3(0.2,0.5,0.2); if(res.y == 2.) col += vec3(0.5,0,0); if(res.y == 3.) col += vec3(0,0.5,0.5); ``` 加了着色后的效果为: 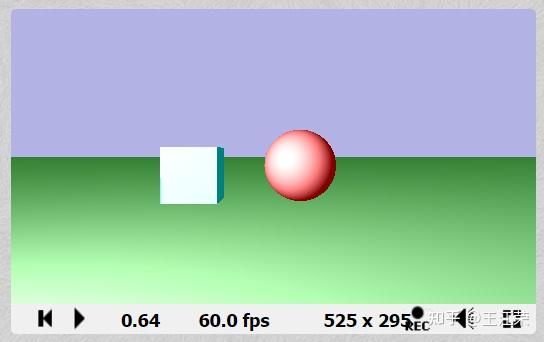 是不是有那味了。但是还差点,因为我们还没有阴影。 硬阴影 --- 硬阴影的原理想必大家都很清楚,即我们的着色点能被摄像机看见,却不能被点光源给看见。例如我们例子中光源在左上角,那么下图中几个标记了的黑点就属于光源看不见,摄像机能看见的点,那么我们就应该在这些点添加阴影。  那么我们怎么判断这些点不能被光源所看见呢?最简单的方法依旧是 raymarching,我们从光源往着色点发射一根射线,当这根射线打到物体表面时射线长度正好是光源到着色点的长度,那么就代表光源能够看见该着色点,否则则看不见。 ``` //计算硬阴影 bool calHardShadow(in vec3 orign, in vec3 direction, float lenMax) { float len = 0.; for(int i = 0; i < 70; i++) { vec2 d = map(orign + direction * len); if(abs(d.x) < (0.001*len)) { if(lenMax > len + 0.015) return true; break; } len += d.x; } return false; } ```  完整 Demo ------- [undefined](https://www.shadertoy.com/view/7dXSDl) Shader中使用距离函数(Distance Function)绘制二维图形 直线与三角形的重心坐标(Barycentric Coordinates)的推导与应用