光栅化过程中的采样与反走样(MSAA),频域与滤波 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/363284887) 采样(sampling) ------------ 何为采样?是指从总体中抽取个体或样品的过程。用程序的思维来解释的话,就是给定一个连续的函数,然后我们通过不同的输入来获取函数的值。例如有个函数 y = f(x) ,我们分别求 x = 1,x = 2,x = 3... 时 y 的值。**采样即把一个函数给离散化(Discretize)的过程**,在图形学中有广泛的应用,例如在[光栅化过程](https://zhuanlan.zhihu.com/p/363245957)中取每个像素的中心点,就是在采样。 ### 采样频率 采样频率可以理解为抽取样本的间隔,例如上面我们采样的是 x = 1,x = 2,x = 3...,间隔为 1。如果改成 x = 1,x = 3,x = 5... ,间隔为 2,那么就代表频率变慢。而改成 x = 0.5,x = 1,x = 1.5... ,间隔为 0.5,那么就代表频率变快。 应用到光栅化里的话,我们可以把每个三角形当做是无数个点组成的,而我们的屏幕又由一个个的像素组成,这些像素的中心点对应到三角形中的某些点,等同于所有点中所抽取出的样本。那么采样的间隔自然是我们像素的实际物理大小。因此若屏幕大小不变,分辨率越高(即像素越多,像素的中心点物理间隔越小),采样的频率越高。 上面介绍的属于采样二维空间中的位置信息,此外我们还可以**采样时间**,例如下图,便是采样了不同时间人挥球的动作,进行了显示。  走样(Aliasing) ------------ 走样,什么是走样?汉语字典给的定义是:变样,失去原有的样子。这个就很好理解了,我们光栅化一个三角形,得到的结果因为锯齿导致它变样了(如下图),那么锯齿就是我们走样的一种体现。 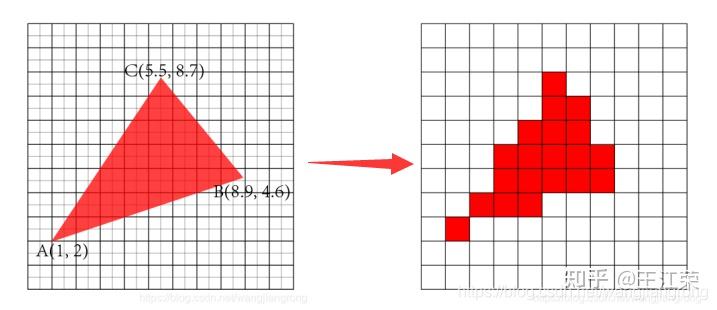 锯齿与采样的关系 -------- 从图中我们可以看出,导致锯齿的原因是由于每个像素内只存在一种颜色,同时每个像素又有一定的大小,这些锯齿就是在三角形边缘的一个个像素。因此若我们的像素越大那么锯齿也就越大越明显,像素越小锯齿也就越小越不明显。 回到采样上,因为我们在光栅化操作时,采样的是像素的中心点。那么像素越小,说明像素的中心点越密集,也就是说我们的采样频率越高。也就是说**锯齿出现的原因是因为我们的采样频率不够高**。 但是上面所说的提高分辨率来提高采样频率其实是属于物理 / 硬件层面上的优化了(直接换屏幕了),若我们要在分辨率不变的情况下做抗锯齿操作呢?也就是我们后面要介绍的**反走样**操作。 像锯齿这样,由于采样所造成的一些问题,在图形学中我们称之为 **Sampling Artifact**,这些问题造成的现象也就是**走样**。 Sampling Artifacts(瑕疵)in Computer Graphics ------------------------------------------ ### 锯齿(Jaggies) 我们前面提到的锯齿就是采样产生的一种问题。  ### 摩尔纹(Moire) 摩尔纹是一种会使图片出现彩色的高频率不规则的条纹,也是采样所造成的问题之一。我们生活中使用手机拍摄显示器屏幕的时候,拍出的照片往往就好出现扭曲的纹理,其实就是摩尔纹。 我们要在图像上进行复现也很简单,我们把屏幕上的一张大小为 m* n 的图去掉所有奇数行和奇数列的像素,然后把剩下的像素重新拼接在一起(等于缩小了图片),然后依旧按照原始的 m*n 大小显示,就会出现摩尔纹。例如下图:  用采样理解起来也很简单,例如我们一个 2*2 的 4 个像素,原本采样 4 个点,四个点颜色不尽相同,去掉奇数行奇数列后只剩右上角的 1 个像素,然后又要显示成 2*2,那么就是四个像素都变成了一个颜色,也就是右上角那个像素的颜色,等同于只采样了右上角 1 个点。 也就是说原本我们每个像素采样一次,变成了每四个像素采样一次,使采样频率降低,这种情况我们称之为**欠采样**(Undersampling)。 ### 车轮效应(Wagon wheel effect) 在生活中,有些高速行驶的汽车,但是我们的眼睛看它的车轮却反而像是在倒着转,这也是采样所造成的问题,我们称之为车轮效应。  造成这个问题的原因是人眼在时间上的采样,跟不上运动的速度,时间上采样慢也就是采样频率低。 造成走样的原因 ------- 从上述种种 Sampling Artifacts 造成的走样来看,都是由于采样频率低(采样慢)跟不上物体的实际变化速度。更专业的说法是,**信号(Signals)变化的太快(高频,high frequency),而我们的采样太慢**。 这里的信号变化怎么理解呢?车轮效应我们很好理解,信号变化快就是车轮转的太快了,随着时间的变换,车轮的旋转角度发生了变换。但是对于光栅化过程,怎么理解这个信号变化呢? 我们前面讲过光栅化是把真实的场景映射到屏幕上的过程。我们可以把真实的场景内容看作是一个由 m*n 个像素组成的(忽略 z 轴),m 和 n 趋向于无限大,为了方便理解和描述,我们称它们为原始像素。那么我们的光栅化等于把这 m*n 个像素进行缩减,使其显示在 x*y 个像素的屏幕上,x 和 y 远远小于 m 和 n,我们称之为屏幕像素。简单来说,我们等同于把一幅高精度的图像(现实)变成了一幅低精度的图像(图片),这里的信号,我们可以称之为**图像信号**,信号变化就是原始像素中每个像素间的颜色变化,颜色本质就是一串信息,例如 RGB 值。同时也说明**图像的信号变化并不是随着时间而变换,而是随着空间中 x 和 y 的值的变化而变化**,这种我们称之为**空间域**(Spatial Domin)。那么信号变化快就是指原始像素间颜色发生了骤变,例如白色变成黑色等,反之两个像素之间颜色没有发生什么变化就是信号变化慢。 这也就很容易理解走样的说法了,如果信号变化慢,即周边一群像素的颜色相似,那么我们采样慢,即只取其中一点,就不会造成什么问题。但是若信号变化快,周边一群像素都是五花八门的,我们采样慢就会造成走样。这也是锯齿为什么都发生在三角形边缘的原因,因为在三角形内部信号变化慢,但是在三角形边缘信号变化往往会骤增。 反走样(Antialiasing) ----------------- 既然我们的采样结果走样了,那么我们就要做一些优化来尽量的避免走样,也就是反走样操作。 例如我们平时玩游戏,在画质设置里往往就会有抗锯齿的操作(即反走样),如下图是最近在玩的 GTA 和塔科夫的抗锯齿设置。  本文后续主要会介绍 MSAA 的原理,了解了反走样后,我们也能对各种游戏的抗锯齿设置有一定的了解。 ### 模糊操作(Blurring) 针对我们前面光栅化一个三角形的反走样操作为,在我们采样之前,先对图形进行一个模糊的操作,如下: 原本的光栅过程,如下图,采样后的像素颜色要么是红色要么是白色 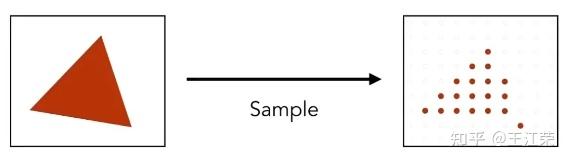 加了模糊操作后的光栅过程,如下图,可以看出经过模糊处理后,三角形的边缘颜色变化有了一定的过渡,根据前面所说的,就是信号变化变慢了。然后再采样的时候就不再全是红色或白色,也会出现不同程度的淡红色。  ### 实际效果 下面两幅图便是通过模糊后进行采样,图中可以看出实现了一定的抗锯齿 / 反走样效果。  ### 思考 前面我们的操作时先做模糊再做采样,那么我们是否可以先做采样再做模糊操作呢?答案是否定的,具体原因我们在后续介绍滤波的时候解释。  注:对于先采样后模糊的操作我们称之为 **Blurred Aliasing**,即把走样后的图像进行了模糊操作。 那么为什么呢?为什么可以通过模糊操作来实现反走样,又为什么模糊和采样操作不能逆转过来呢?这里首先就需要我们对信号与频域进行了解了。 信号与波形 ----- 在前面,我们说过我们采样,采样的是信号(也可以称作是函数),而波形则是信号的表现形式。 我们来看看最简单的两个信号波,分别是正弦波 sin(2πx) 和余弦波 cos(2πx),如下图: 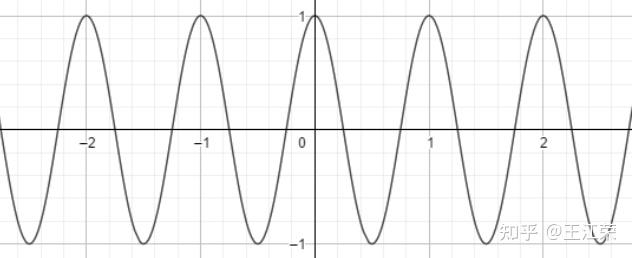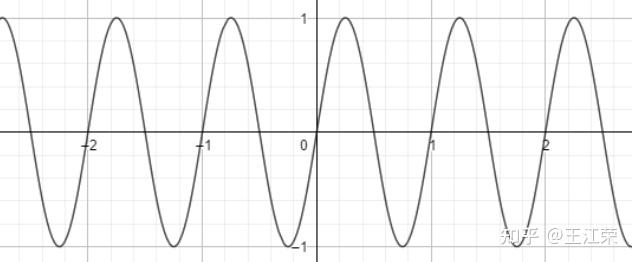 这两个波是在**时域**(Time Domain)中定义的,也就是信号随时间的变换而变换,图中的 x 轴代表着时间。 周期和频率(Frequency) ---------------- 从上图中,我们可以看出不管是正弦波还是余弦波,我们都可以发现它是一直在重复的信号,而每次重复,我们就称之为一个周期(T)。例如正弦波 sin(2πx),它每隔 x=1 的时段进行一次重复,我们可以称之为周期为 1 的信号波(T=1)。 若修改其 x 前的系数,例如变为 sin(4πx),那么得到的波形会变为下图这样  可以发现该正弦波每隔 x=0.5 重复一次,即周期 T=0.5。从图中也可以发现,此时正弦波变化的更快了。 理解完周期后,那么频率又是指什么呢?频率(F)是单位时间内完成周期性变化的次数,也就是说 F=1/T 。例如 sin(2πx) 的频率 F=1,sin(4πx) 的频率 F=2,频率越大,变换也越快。因此频率是描述周期运动频繁程度的量。 同时**对于图像信号而言,我们认为两个像素间的颜色变化大则代表频率高,反之则是频率低**。 频率与采样 ----- 前面我们说到,走样是因为信号变化快(频率高),而采样的频率低导致的。那么我们现在来通过波形来更直观的看一下走样现象,如下图,我们有三个不同频率的信号(从上到下频率变高),然后我们每间隔 x=1 进行采样一次,就会得到图中的各个点。  采完样后,我们自然是要根据我们的采样来恢复原始信号。也就是我们把这些采样点进行连线,就是我们能够恢复出来的原始信号,如下图。  结果很明显,频率慢的信号和我们的采样恢复结果基本一致,但是频率高的信号就不行了,就出现了严重的走样现象。 同时还可能出现信号完全不同,但是采样结果却完全相同的情况,例如下图,黑色和蓝色波形分别代表着两种不同的信号,但是它们的采样结果(图中的白点)却相同。  以上种种问题都是采样频率不足而导致的。 频域(Frequency Domain) -------------------- 前面我们说到时域,是信号在不同时间的状态,即 函数 f(x) 中,x 值代表着时间。空间域,是信号在不同位置的状态,即 函数 f(x) 中,x 值代表着偏移量。顾名思义,频域就是指**在不同的频率下观察信号**,即 函数 f(x) 中,x 值代表着频率。画成坐标系的话,横坐标代表着频率,画出来的图形我们称之为**频谱**。 那么在频域上观察有什么好处呢?这个我们在后面介绍。 既然我们要在频率上观察信号,那么就要把原来时域或者空间域的函数转换成频域的,那么如何转换呢?傅里叶变换可以帮助我们。 傅里叶变换(Fourier Transform) ------------------------ ### 傅里叶级数展开 生活中的很多信号,并不像正弦波余弦波这样简单清晰,例如我们前面所说的图像信号。 就像我们前面处理物体表面一样,把一个表面划分成多个不规则的三角形。对于信号,我们也可以沿用这样的思想,将其进行拆解。法国数学家傅里叶发现,**任何周期函数都可以用常数与正弦函数(和 / 或)余弦函数构成的无穷级数来表示**,这种展开方式我们称为傅里叶级数展开。 参考: [为什么傅里叶变换可以把时域信号变为频域信号?](https://www.zhihu.com/question/279808864/answer/552617806) 例如我们有如下波形(**方波**)的一个函数:  可以看出它是一个周期性函数,那么我们怎么用正弦余弦函数来表示它呢? 首先从图中我们可知,该函数的周期为 4W。而我们 cos(2πx) 的周期为 1。那么,我们首先要使他们周期是一样的,即可得到  。 周期相等后,我们要使其高度也相仿(注意,这里不是相等),图中可以看出波形的高度为 H,而 cos(2πx) 的高度为 2,因此我们会再乘以一个  ,即得到  ,其波形如下图红线:  注:本例子中用到的一些值,我们暂时不考虑为什么使用这些值,我们只需要知道使用这些值后可以产生的效果即可。 我们再进行向上平移  ,即  ,如下图,是不是就有点像原来的波形了  接下来我们有个函数  ,如下图蓝色波形。(红色蓝色频率不同)  我们把红色和蓝色相减,即  ,此时红色波形变为下图 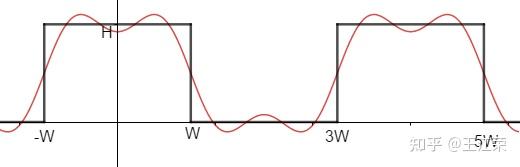 相比之前更加像黑色波形了一点。若我们再进一步处理,如:  ,效果如下: 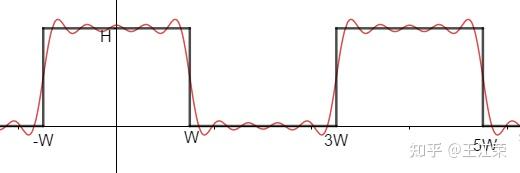 可以发现更加接近了,可以得出结论,若我们无限往下加,红线就会无限接近于黑线。黑线代表的就是我们任意一个周期函数,而红线则代表着若干个余弦函数与常数,证明了傅里叶展开的可行性。 在这个例子中,每一项 cos 函数都是频率不相同的,也就是说**傅里叶级数展开,展开成了多个不同频率的正弦或余弦函数**。 ### 傅里叶变换 傅立叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。 它可以帮我们**把一个时域或者空间域的函数 f(x) 变换成 频域上的函数 f(w)**。同时我们也可以通过频域上的 f(w) 变换回时域或空间域上,这个过程称之为逆傅里叶变换。整个过程如下图: 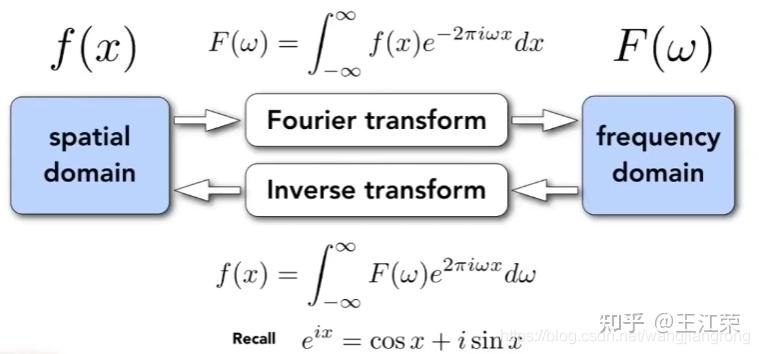 注:关于这个看着很复杂过程,在这里我们不用清楚他的推导以及原理,只需要知道有这么个公式可以帮助我们即可,我们也可以通过各种相对应的 api 来帮我们实现转化。 图像转换成频谱 ------- 前面我们说过,一个时域或空间域上连续重复的信号可以通过傅里叶变换变到频域上。而图像本身就属于空间域上的一种信号,因此我们也可以通过傅里叶变换使其变成频域的表现形式。如下图,左边是一张图像,右边是傅里叶变换后的频谱。  对于右图的解读:**图像中心代表着低频率区域,越往外频率越高**,图像周围即是高频率区域。同时**亮度越亮,说明该频率的信息越多**,例如图中中心最亮,往外越来越暗,说明原始图像中低频信息最多,高频信息偏少。而关于图像的频率信息也就是像素间颜色变化,颜色变化越大则频率越高。同时我们也可以通过逆傅里叶变化,将右图变回左图。 我们说重复的信号才能被变换,但是图像的信号怎么看也不像是连续信号。这里我们会把图像做一个**平铺**处理,也就是无数张相同的图片连接在一起,这样每一张图片就是一个重复的信号。 我们可以把之前傅里叶级数展开例子中的每个凹凸形状的信号当做是一张图片,无数个重复的凹凸形状就是无数张图片。每个凹凸形状通过级数展开变成了无数个频率不同的正弦或余弦函数,那么**每张图片也可以展开成不同频率的信号,这些信号就会根据频率,显示在我们的频谱中**。 并且频谱中水平和竖直方向各有一条很明显的线就是由于平铺导致的,因此是图片连接在一起,因此图片的右边界连接的是图片的左边界,下边界连接的是上边界,此处往往会导致出现大量的高频信息。 滤波(Filter) ---------- 滤波,顾名思义,过滤信号波,根据什么过滤呢?就是我们的频率。 ### 高通滤波(High-Pass Filter) 高通的意思就是高频可以通过,高通滤波也就是过滤掉低频的信号。如下图,我们去掉低频信号后得到的图像。 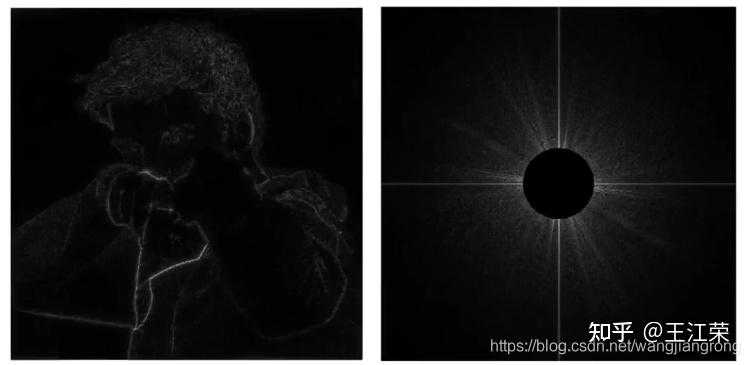 可以看出,过滤掉低频信号后,我们能看清的就剩下人物的边界了。这也是因为往往在边界处,会发生较大的颜色变化。 ### 低通滤波(Low-Pass Filter) 有高通滤波自然也有低通滤波,即过滤掉高频的信号,如下图,图像变得模糊了,因为原本清晰的边界都被过滤掉了。  ### 带通滤波(Band-Pass Filter) 带通滤波,允许特定频段的波通过。例如下两图 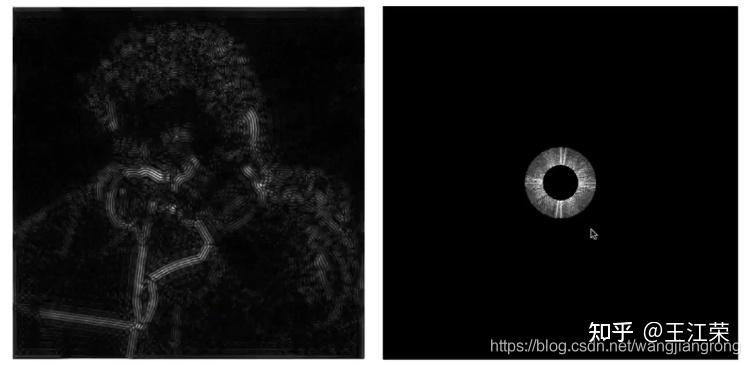 卷积 (Convolution) ---------------- 从上面的例子中可以发现,所谓滤波的过滤似乎并不是对于某些频率的信号直接抛弃不要,而是把它变成了一个新的信号(低通滤波比较明显,因为如果是直接抛弃某些信号,那显示出来的就是黑色)。并且原本我们一个 m*n 的信号通过滤波过滤后,依旧还是一个 m*n 的信号(图像大小没有发生变换)。这是因为**滤波的本质是将信号与滤波器在时域上进行卷积的操作**。 何为滤波器?我们可以把滤波器看作是一个**固定大小的信号**,可以是 1*3,3*3 等等。然后滤波器中的每个信号都有一个对应的数值,滤波器也被称之为**卷积核**。 何为卷积操作?假设我们有一段信号,要使用 m*n 大小的滤波器进行滤波。当对其中第 x 个信号进行滤波时,实际上是以第 x 信号为中心点,取其周边 m*n 个信号,与滤波器中的各个值一一对应相乘,然后相乘后值全部相加,得到的新值便是第 x 个信号进过滤波后的值。 如下图,我们将一段信号使用 3*1 的滤波器进行滤波操作: 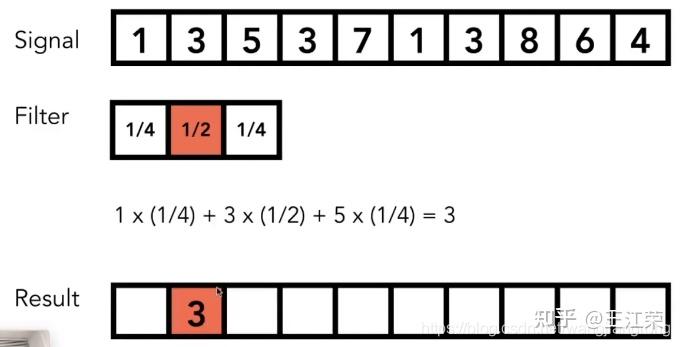 如图,我们将第二个信号进行 滤波 / 卷积 操作,因为滤波器是 3*1 的,因此我们以第二个信号为中心,取 3*1 的信号,即第 1-3 的信号。然后与滤波器各个值相乘然后相加,得到的结果如图。 那么若是第一个或者最后一个信号怎么卷积操作呢?例如第一个信号,左边并没有信号去对应滤波器的第一个值了。对于缺省的信号我们**自动补零**即可,例如第一个信号取得的 3*1 的信号值分别为 0,1,3,然后进行卷积操作即可,得到的结果为:(0 * 1/4) + (1 * 1/2) + (3 * 1/4) = 1.25。 图像和卷积 ----- 了解了卷积操作后,也就很容易理解前面对图像做滤波操作的原理了,即新图像中第 (x,y) 像素的值,是原本图像中第 (x,y) 像素和其周边几个像素与滤波器进行卷积操作的值。 如下图,我们把图像和一个 3*3 ,每个值都是 1/9 的滤波器进行卷积操作,得到的就是一张变模糊的图像。因为约等于把几个像素求了个平均,这样颜色偏深的像素会变浅,偏浅的像素会变深,从而相邻的像素变换变小,频率变低。 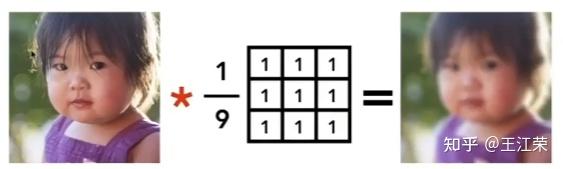 因此上诉滤波器就属于一种低通滤波器,滤波器中所有值的和为 1。 同时我们也可推导出,若我们使用 10*10 的滤波器,每个信号的值为 0.01,那么图像就会变得更加模糊,因为更多的像素参与了卷积操作。 这样也很容易理解其他的一些滤波器,例如高通滤波器如下: 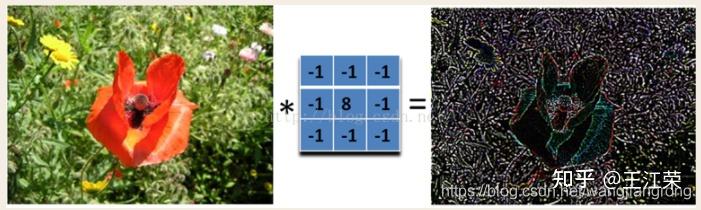 可以发现该滤波器中所有值的和为 0。也就是说颜色越相近(低频)的几个像素,得到的结果越接近于 0,即黑色。 关于其他滤波器可以参考这篇文章: [知者:图像处理基本知识(理解卷积非常有用)](https://zhuanlan.zhihu.com/p/55013828) 是不是很神奇,似乎有点明白 PS 各种效果的原理了。 频域和卷积 ----- 前面我们可以发现卷积操作是在时域或者空间域上进行的,那么对应到频域上,是怎么计算的呢?如下图:  我们前面说过滤波器也可以看作是一个信号,因此它也可通过傅里叶变换变到频域上,例如上图的低通滤波器,由于每个信号一样,因此都是低频信号,得到的频域自然是中间亮外面黑。然后将它与傅里叶变换后的图片**相乘**,即可得到对应的结果。 因此**时域上的卷积相当于频域上的乘积**,同时反过来也是成立的,即**时域上的乘积相当于频域上的卷积**。 采样与频域 ----- 注:这块内容比较抽象,同时需要较多的信号学相关的知识,我们这边只做结果论。也就是知道什么操作会得到什么结果即可,具体推导过程暂时不做深究,因为本人作为萌新也不太懂,希望有大神指点。 ### 冲激函数 如下图,前面我们说了信号就是一个函数,而采样就是在该函数的各个点取值,如下图,虚线便是我们的取样点。  而对于这样的采样方式,我们可以理解为,有一个函数,它只在一些特定的地方有值(需要采样),而在其他地方的值都为 0(不需要采样),这样的函数我们称之为**冲激函数**。 例如最简单的冲激函数即为:  代表着 t=0 时有值(无穷大)而 t 为其他值时,结果都为 0。 ### 采样与函数 前面说了信号是一个函数,采样是一个冲激函数,那么采样后的结果在这里我们就可以理解成这两个函数相乘所得到的结果。  如图,a 函数代表信号,c 函数为冲激函数代表采样,两个相乘得到 e 函数,即采样结果,也就是信号上各个点的结果。上述就是在时域上的采样原理。 ### 采样与频域 那么采样在频域上是一个怎么样的过程呢?我们知道一个信号可以通过傅里叶变换变到频率上,如下图  a 是我们时域上的信号,b 是我们频域上的信号。前面我们说过频域是在频率上观察信号,因此 b 中的坐标系的横轴代表着频率,同时越往外代表频率越高。从 b 中我们可以看出,信号 a 大部分还是低频的信号。 接着我们的冲击函数同样可以做一个傅里叶变换,得到的截图如下,c 为我们的冲激函数,d 为该函数的频谱。(具体为什么变成这样我们这里暂时不做过多的推理)  从中可以看出,将冲激函数傅里叶变换后以及还是冲激函数,只不过间隔发生了变化。 前面我们说过在时域上是两个函数相乘,同时前面我们也学到了时域上的乘积等于频域上的卷积,因此在频域上,我们要把 b 和 d 进行卷积,得到的结果如下,e 为 a 和 c 在时域的乘积结果,f 为 b 和 d 频域的卷积结果。  可以发现,得到的频域结果就是把原本频域的信号进行重复,因此可以得到结论**采样就是在重复信号的频谱**。 频谱和走样 ----- 从前面我们知道采样是根据冲击函数的频谱间隔在重复信号的频谱,那么就会存着这么一个问题,**冲击函数的间隔小于频谱的大小**,如下图:  可以发现,这种情况就会造成一部分的频谱重叠,这就是我们所谓的走样现象。因此**在频域角度上,走样就是频谱重复时发生了混合**。而重叠的这部分就是我们的高频信号,因为前面 b 中我们可以看出,一个信号的频谱图外面代表着高频信号,而重叠部分就是外面的这部分。 频谱和反走样 ------ 那么解决方法是什么呢?最简单的自然是增加频谱中冲激函数的间隔,使其避免重叠现象。通过前面的学习,我们知道采样频率越高,即时域上的冲激函数间隔越小,走样越少,因此我们也可推出,**冲激函数在时域间隔越小,在频域上则间隔越大**。 当然了,增加采样频率是最容易理解的解决办法,但并不是最简单的,因为例如一个固定分辨率的屏幕,我们没法更改他的分辨率,即采样频率。那么应该怎么做呢?此时我们可以去除掉这些会被重叠的信号,如下图:  我们把原始信号的频谱的两头(即高频信号)去掉,然后依旧按原来的间隔排列,就会发现重叠的部分消失了。 **这也就解释了为什么前面所说的先做模糊操作再采样可以实现反走样,因为模糊操作等于做了个低通滤波,即去掉了高频的信号,减少了信号重叠的情况。** **同时先采样在模糊的话,在频域上,采样后频谱已经混叠了,此时再去掉高频信号,等于是把混叠后的结果去掉两端(并不是每一段去掉两端),所以是错误的。** 模糊操作怎么做 ------- 既然反走样可以通过先模糊再采样的操作来实现,而采样的操作在上一篇我们已经知道如何实现了,那么模糊操作应该如何实现呢? 前面我们说,采样可以看作是把由无数个很细小原始像素组成的真实场景,通过取特殊点的方式,把它映射到有固定数量固定大小的屏幕像素上。因为是先模糊后采样,那么就等于我们要对原始像素的图像信息进行模糊操作。 而模糊操作我们前面也说了,它属于低通滤波,即是一个 n*n 大小且每个信号值为  的滤波器,也就是说一个原始像素模糊后的值,是它和它周边 n*n 个像素的值,求个平均。 我们知道一个屏幕像素会对应很多很多的原始像素(设 m*m 个),那么我们设想下,如果把一个屏幕像素所对应的所有原始像素的值求个平均,那么得到的这个值,不就是中心的那个原始像素,与 m*m 的滤波器做一次模糊操作的值么。 也就是说我们的模糊操作,只需要把一个屏幕像素内的所有颜色求平均即可,如下图:  第一行即是未做处理时,屏幕像素所对应的原始像素的内容,这些屏幕像素可能在三角形的边界,也可能在三角形内部。第二行即是该屏幕像素内所有颜色取完平均后填充整个像素的效果。 疑问 1:前面说了模糊操作(卷积)是取当前像素和他周边像素的平均值,一个屏幕像素内,例如其左下角 (0,0) 对应的原始像素的卷积结果应该不等于中心点 (0.5,0.5) 对应的原始像素的卷积结果,因为他们周边的原始像素只有四分之一是共同的。可是上图中明显把屏幕像素所对应的所有原始像素颜色都变成了中心点的卷积结果了,这不是错误的么?严格意义来说,这个模糊操作确实存在问题,但是结合到后面我们的采样过程,就会发现可以这么操作。因为我们的采样过程只采样屏幕像素的中心点所对应的原始像素,所以你屏幕像素其他点到底是什么颜色,我们在采样过程中压根不关心。然后会根据中心点的颜色去填充整个屏幕像素,实际上现在整个屏幕像素就已经都是中心点的颜色了。因此做完上面的操作我们甚至等于完成了采样的操作。 疑问 2:例如上面图片的模糊操作中,怎么算出一个屏幕像素内的颜色平均值?也就是怎么通过图片中的第一行得到第二行的结果(当然了,肯定不能通过肉眼观察,例如你看第一行第二个图,黑色白色各占了一半,那么平均值肯定是 0.5)。解决方法就是接下来我们要学的 **Supersampling** 的概念。 疑问 3:前面我们说了,先模糊再采样,但是模糊操作后,首先这个三角形形状大小都可能变了,怎么确定像素和它位置关系?其次就算能确定是否在三角形内,三角形的颜色也不是单一的一个颜色了(边缘因为模糊操作颜色变淡),那怎么采样像素中心点的颜色(我们之前采样颜色是通过采样点和三角形的位置关系来确定的)?其实在疑问 1 的最后一句提到了,做完模糊后,我们不需要再采样了,因此也就不存在疑问 3 的操作了。 MultiSampling Anti-Aliasing(MSAA) --------------------------------- 其实对于上面的问题 2,解决方法很简单,只要我们屏幕像素有足够多的采样点,那么就可能覆盖到所有的原始像素。然后我们只需要知道这些采样点分别与三角形的位置关系即可。例如我一个屏幕像素里面平均分布 100 个采样点,采样点的位置我们也都可以算出,也就可以知道它们和三角形的内外关系,那么如果这 100 个采样点有 30 个在三角形内,那么就可以说明这个屏幕像素的内容大概有 30% 是三角形颜色,剩下 70% 是背景色,即可求出平均颜色。采样点越多,结果就越准确,当然了,这会复出极大的计算代价。因此在实际操作中,我们可能只会数量较少的采样点来计算这个平均值。相比只采样屏幕像素的中心点,这种方式多了几个采样点,因此我们称之为**超采样**(Supersampling),如下图,为 4*4 的超采样  普通采样和超采样的对比效果如下:  通过超采样,我们就可以计算出每个像素的平均颜色,如下图:  然后将这些颜色填充其对应的整个像素即可。这里就不再需要做采样中心点的操作了,因为中心点的颜色肯定和我们前面计算出来的平均值颜色相同(也解释了上面疑问 3 的问题)。 MSAA 虽然增加了采样点,但是它为的检测三角形在一个像素内的覆盖情况,也就是为了做模糊操作。但是后续的采样(虽然不用做了)依旧还是每个像素的中心点,因此它不属于通过改变采样频率来实现反走样的操作。 前面也说了使用 MSAA 增加了采样点,那么自然而然,计算量也就增加了很多。因此为了更好的性能同时能够实现反走样,也对 MSAA 进行了很多的优化。例如增加的采样点并不是均匀分布的,而是按照一定的规则摆放,或者有些采样点能够被复用等等。 除了 MSAA 外,现代图形学还有各种各样的反走样操作,其中最具代表性的就是 FXAA 和 TAA(在我们前面游戏设置的截图里也能看见它们)。 FXAA(Fast Approximate Anti-Aliasing) ------------------------------------ 先得到带有锯齿的图,然后通过一些图像匹配的方法找到这些锯齿边界,然后将这些边界换成没有锯齿的边界,属于图像的后期处理。 时间抗锯齿,TAA(Temporal Anti-Aliasing) --------------------------------- 将采样点从单帧分布到多个帧上,使得每一帧并不需要多次采样增加计算量。 光栅化与深度缓存 着色与Blinn-Phong反射模型