变换与矩阵 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/362551995) 什么是变换? ------ 变换,其实都是将一个输入的值,进过一些操作,变成一个新的输出值。例如输入一个点的位置 0,最后输出其位置 10,即发生了移动变换。由这一个特性也可得出,所谓的**变换其实就是函数**。 > 输入值 x -> 变换( 函数 f(x) ) -> 输出值 x 而使用变换是为了让我们以**运动**的方式去思考,例如前面提到位置 0 变为 10,我们要想成是从 0 慢慢移动到 10,并不是一下子变为 10。 在**线性代数**中,变换考虑的是一个**向量**的输入以及输出,向量的起点都为原点,例如将向量 (2,4) 缩放 0.5 倍,即得到向量(1,2)。 对于一个整个空间(称之为**线性空间**或**向量空间**),我们可以看作空间内有无数个点,而原点到每一个点的连线即为一个向量。空间的变换即空间中每一个向量都移动到对应输出向量的位置,也可以看作是空间中的每个点移动到变换后的目标位置。 例如下图,便是一个简单的空间旋转变换,向量 (0,1) 旋转后变为(1,0)。 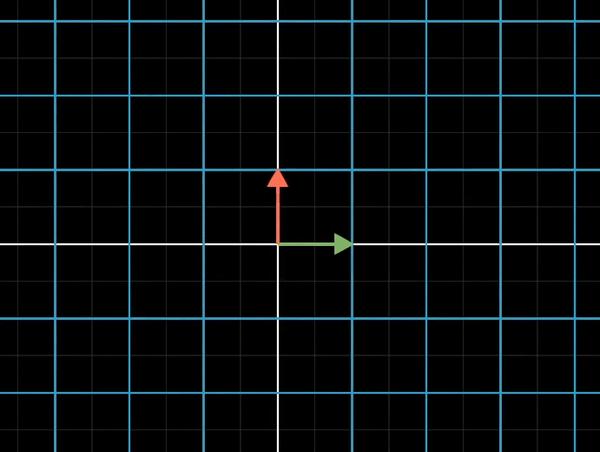 接下来我们来看一个比较复杂的变换,如下图,为**复平面**上  的变换: 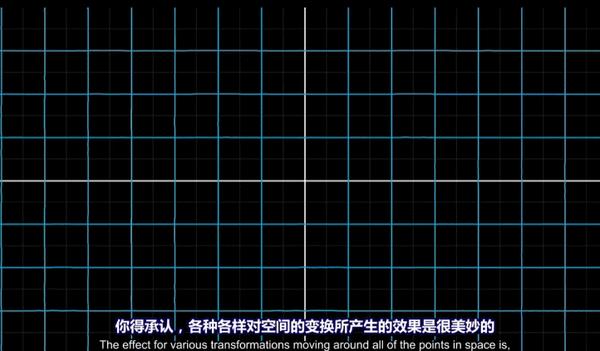 注:gif 来源:[线性代数的本质 - 03 - 矩阵与线性变换](https://www.bilibili.com/video/av6043439) 看着很高级,那么它是怎么变换成这样的呢?首先我们要了解何为复平面,简单来说复平面是用来表示复数的,即 a+bi,其中 a 和 b 为实数,i 为虚数(即:  )。复平面中 x 轴的值代表着复数中**实部** a 的值,y 轴的值代表着**虚部** b 的值,因此点 (1,1) 代表着 1+i,点 (7,-8) 代表着 7-8i。清楚这一点后,我们就可以通过一些特殊的点,来计算出其变化后的值了,例如: 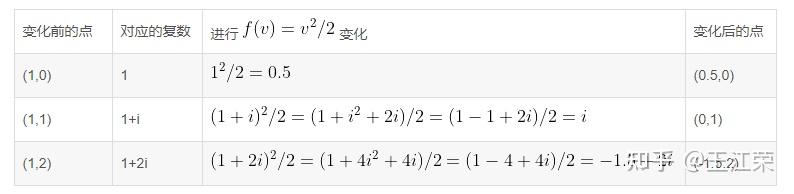 上面其实也就解释了下图中两根黄线的变化前后的缘由。至于为什么要在复平面上,应该是因为如果单纯的只是**向量的平方那是没有意义的**,因为向量是一个 2*1 的矩阵,向量的平方即为 2*1 的矩阵乘以 2*1 的矩阵,根据矩阵的乘法定义,我们知道它们无法相乘。 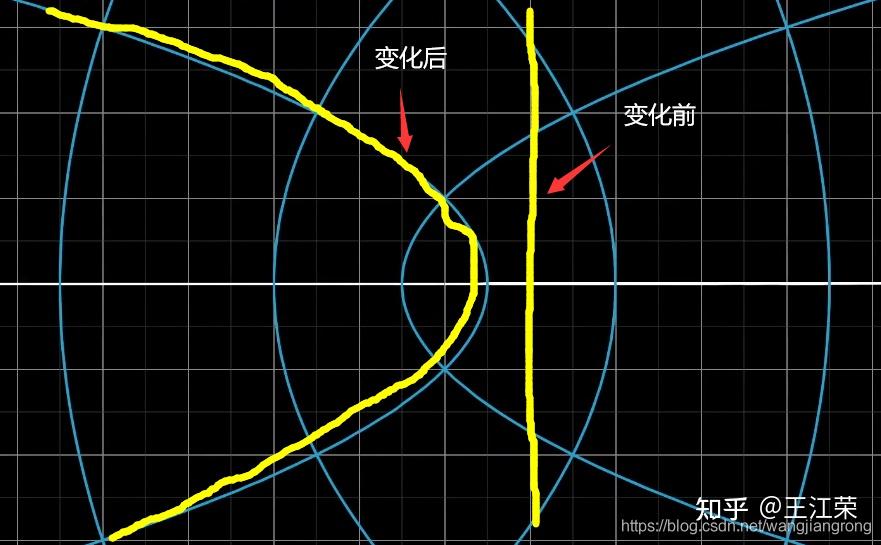 线性变换 ---- 线性代数限制在一种特殊类型的变换上,即线性变换。如果一个变换拥有以下两个性质,我们就称它为线性的变化: * 直线在变换后仍保持直线,不能有所弯曲。 * 原点保持固定 我们知道变换即为一个函数,我们假设这个函数为 f(x) ,那么站在数学的角度上,如果同一个空间中的任意两个**向量**  和  ,以及**数域**中的一个数 k(可以简单的理解为 k 为一个实数),满足以下条件的话,函数 f(x) 即为线性变换: *  *  例如 f(x) = 2x ,代表着一个放大两倍的变换,设  ,  ,那么  。 可得到  ,  ,  ,满足第一条定则。 设 k=3,那么  ,  ,满足第二条定则。 因此该变换为线性变换。 ### 推导 在二维空间中,设两个基向量  ,  那么任意一个向量  都有  。当空间发生线性变换后,所有向量都会发生变换,包括我们的基向量。假设变换后  ,  ,根据线性变换的那两个性质,那么变换后的  即等于  我们把它写成矩阵的形式: >  到这一步我们发现,我们输入的向量为  ,输出的向量为  ,学习了矩阵的乘法后会发现,这个结果不就是矩阵  乘以  的值。 **因此线性变换的本质即是一个矩阵与向量的相乘,**所有二维的线性变换都可以通过下面表达式来表达: >  **并且矩阵**  **中的**  **和**  **即为**  **变化后的值,** **和**  **即为**  **变化后的值**。 若没有发生变换,那么  就等于  也就是单位矩阵,单位矩阵乘以任何向量依旧是该向量本身,即没有变换。 若向量为零向量,即  那么任何矩阵乘以它的结果依旧为  ,验证了线性变换的原点不变性。 二维变换 ---- 接下来我们先从二维空间入手,来看看常见的变换及其对应的矩阵。 ### 缩放  设缩放比例为 s,那么 (1,0) 缩放后为 (s,0),(0,1) 缩放后为(0,s),所以我们的矩阵为,该对角阵也称为**缩放矩阵**。 >  ### 思考 如下图,缩放后的应该是情况 1 还是情况 2 呢?  从图中我们可以看出,情况 1 是以坐标点 (2,2) 为原点进行缩放,而情况 2 是以坐标点 (0,0) 为原点进行缩放,那么哪种是对的呢? 我们可以想象一下,图中的坐标系是一部手机,坐标系中的小方块是手机中的后置摄像头,有如下几种情况。 1. 假如我们以手机的中心(即坐标系原点)缩放整个手机,那么情况 2 是对的。也可以用向量来验证,  从 (1,3) 变为了 (2,6),属于线性变换。 2. 假如我们以摄像头的中心(即坐标系的 (2,2))缩放整个手机,那么情况 1 是对的。但是这种情况手机的中心点坐标也发生了移动(从(0, 0) 变到了(-2,-2)),不符合线性变换原点不动的性质,因此他不是一个线性变换。它属于一个复合变换,平移 -》缩放 -》平移,后续会介绍到。 注意:后续介绍到的几种变换也都会有一样的情况,例如对称可以以 y 轴对称,也可以以 x=1 的轴对称,旋转可以以原点旋转,也可以以其他任意点旋转。但是我们后面介绍的几个变换的前提都是线性变换,因此都是以原点或者原点相关的轴进行变换。 ### 对称 若是沿 y 轴对称,那么 (1,0) 变为 (-1,0),(0,1) 不变,那么矩阵为  >  同理若为沿着 x 轴对称,矩阵则为  ### 切变 如下图,即为一种切变(空间中所有的竖线以与 x 轴的交点为中点进行倾斜)  可以发现 (1,0) 在切变后保持不变,(0,1)在切变后变为(a,1),a 即为切变的偏移量,上图中 a=1。 因此切变的矩阵为  >  ### 旋转 设我们的线性空间逆时针旋转 θ 度,通过三角函数我们可以知道,(1,0) 变为 (cosθ, sinθ),(0,1) 变为 (-sinθ, cosθ) 因此逆时针旋转 θ 度的矩阵为  ### 平移 平移是一个非常特殊的变换,我们知道若一个点 (x,y) 在坐标系上平移 (i,j) 后的位置为 (x+i,y+j),但是对于向量而言,(x,y)无论怎么移动始终都是 (x,y),例如两个初始向量(0,1) 和(1,0)平移后依旧不变(转换为矩阵就是单位矩阵),因为向量拥有**平移不变性**。 因此平移变换的表达式应为一个向量加上一个偏移向量,而不是矩阵与向量的相乘了,如下: >  该表达式也无法用矩阵相乘的方式来表示,因为  的两个方程式为 ax+by 和 cx+dy,a,d,b,c 无论如何取值都不可能等价于 x+i 和 y+j。因此**平移变换不是线性变换**。 ### 仿射变换 理解线性变换和平移之后,仿射变换理解起来就非常的简单了。仿射变换即先做一次线性变换,然后再做一次平移变换,其表达式如下: >  齐次坐标 ---- 那么有没有什么方法,可以通过一个表达式就表达好线性变换以及反射变换呢? 聪明的数学家们就此引入了齐次坐标的概念来解决这个问题。直接来看结果(站在巨人的肩膀上的我们通过结果来反推,理解起来会更加的容易),新的表达式如下: >  可以发现当  和  为 0 时,得到的值即为 去掉 1 后就是线性变换的结果。 当  为单位矩阵时,得到的值即为  去掉 1 后就是平移变换的结果。 这样我们就可以**通过一个矩阵** **来表示这些所有的变换**了。 例如: 缩放矩阵:  旋转 + 平移矩阵:  我们会发现原本的向量  被变为了  ,这就是齐次坐标的意义。**齐次坐标会将一个原本是 n 维的向量用一个 n+1 维向量来表示**,在笛卡尔坐标系上的点  引入齐次坐标后写作了  ,例如笛卡尔坐标系上的点  可以用齐次坐标  或者  来表示。因此,与笛卡儿坐标不同,一个点可以有无限多个齐次坐标表示法。 从上面所述,也可得知,若我们有个齐次坐标 那么它对应的笛卡尔坐标即为  ,我们会发现当 w 无限接近于 0 时,x/w 和 y/w 会无限接近正无穷,因此**当 w=0 时,该齐次坐标代表一个无限远的点**。 对于 w 的值,我们还可以进行另一种理解(OpenGL 中也使用了这样的想法),如下: * 当 w=0 时,代表一个二维向量 * 当 w=1 时,代表一个二维的点 前面我们用到的是 w=1 的情况,若我们用 w=0 会出现什么结果呢? >  得到的结果代表一个向量,并且会发现平移的操作没有了,这也表达了向量的平移不变性。 这样**当矩阵和点相乘后表示的还是一个点,和向量相乘后表示的依旧还是一个向量**。 此外在加减法中也具有一定的意义(为了方便就不写成矩阵的形式了,这里简单的写成 (x,y,w)): * 向量 + 向量 = 向量:(x1,y1,0) + (x2,y2,0) = (x1+x2,y1+y2,0) 结果中 w=0,依旧为一个向量。 * 点 - 点 = 向量:(x1,y1,1) - (x2,y2,1) = (x1-x2,y1-y2,0) 结果中 w=0,变为一个向量。 * 点 + 向量 = 点:(x1,y1,1) + (x2,y2,0) = (x1-x2,y1-y2,1) 结果中 w=1,依旧为一个点。 * 点 + 点 = 无意义:(x1,y1,1) + (x2,y2,1) = (x1+x2,y1+y2,2) 结果中 w=2,无意义(实际上等于两点的中点,即 ((x1+x2)/2,(y1+y2)/2) )。 ### 齐次坐标与光照 在 3D 坐标中我们无法表示一个无限远的点,而在齐次坐标中允许有无限远的点(w=0),该属性可以应用在光照的判断上。 我们知道一个点光源的无限远处是平行光,类似于太阳光,太阳是一个点光源,光线到地球后变成了平行光。因此平行光可以通过改变点光源位置向量对应的齐次坐标中的 w 的值来表示,当 w=1 时,即还在点光源的原来位置,依旧是一个点光源;当 w=0 时,即在点光源的无限远处,变为一个平行光。 复合变换 ---- 复合变换即进行多次的仿射变换,例如先旋转后缩放再平移最后切变。 假设向量  经过变换 A,然后变换 B,最后变换 C 后,我们的公式应该写为: >  由于矩阵的乘法不满足交换律(  ),因此上面的式子不能写作  。因此例如先旋转后平移的变换不等价于先平移后旋转。 所以若一个向量经过 ,  ,...  次变换后,其公式为  。其中由于这些变换矩阵都是 3*3 的矩阵(引入齐次坐标),所以相乘后的结果依旧是个 3*3 的矩阵。设 相乘后的结果为  ,那么该矩阵就可以代表上面所有的变换,这个思路可以应用于**矩阵变换的压缩**上,使用一个矩阵代表多个变换。 ### 举例 前面我们的旋转是以原点进行旋转,那么如果我们想以坐标系中的其他点进行旋转,变换的表达式应该是怎么样的? 如下图,便是以点 (2,3) 进行逆时针旋转 45 度的前后变换:  前面我们学习了以原点旋转以及平移的操作,那么我们可以将上面的操作进行分解,如下:  三个步骤对应的矩阵分别为: 第一步,平移到原点:  第二步,逆时针旋转:  最后一步,平移回原处:  结合起来即为:  化简得:  **因此以点 (i,j) 逆时针旋转 θ 角度的矩阵为:**  同理在最前面缩放变换中,我们提到的缩放的情况 1,即可以使用这种情况来解。 逆变换 --- 和一个变换相反的变换,我们称之为逆变换,例如逆时针旋转的变换,那它的逆变换即为顺时针旋转。 假设向量  经过一次矩阵为  变换后变为  ,然后我们可以通过矩阵为  的逆变换使  变回  ,即  。由此可得  (单位矩阵),因此  为  的**逆矩阵**。 因此一个矩阵为  的变换的逆变换,对应的矩阵即为  的逆矩阵:  。 其中有个非常重要的知识点:**旋转矩阵的逆矩阵即是旋转矩阵的转置矩阵**。知道这个后,我们就可以很轻松的求出旋转变换的逆变换矩阵了,即将旋转变换的矩阵转置即可,因为矩阵求逆很难,但是求转置非常的简单,这一点在视图变换中很重要。 那么为什么呢?前面我们知道二维空间中(三维也是同理),我们的变换矩阵都是由 (0,1) 和 (1,0) 两个向量变换后的结果得到的。而这两个向量**都是单位向量,且互相正交**,这不正是我们正交矩阵的性质吗。而选择变换可以保证这两个性质不变,即旋转后,这两个向量依旧都是单位向量,且互相正交。例如若是缩放变换,变换后就不是单位向量了,切变变换,变换后就不正交了。因此我们的**旋转矩阵即为正交矩阵,其逆矩阵就是其转置矩阵**。 例如我们逆时针旋转 θ 度的矩阵  为:  ,那么他的逆变换即为顺时针旋转 θ 度,或者说是逆时针旋转 -θ 度,矩阵  即为  等价于  。 将他们相乘可得  由三角函数可知,  ,所以上面得到的值正是单位矩阵,  为  的逆矩阵,同样  为  的转置矩阵。 三维变换 ---- 前面讲的都是二维空间中的变换,接下来我们来看看三维空间中这些变换对应的矩阵。其中大部分都相似,唯一比较复杂的即是旋转变换,后面单独说。 与二维变换类似,我们可以使用一个 3*3 的矩阵来表示一个三维的线性变换: >  **并且矩阵中的** **,** ** 和**  **即为**  **变化后的值,** **,**** 和** **即为** **变化后的值,****,**** 和** **即为** **变化后的值**。 **仿射变换**的公式为: >  同样的,我们可以通过引入**齐次坐标**来表示仿射变换,公式为: >  例如缩放 s 倍的矩阵为:  三维空间的旋转变换 --------- 相比其他变换,旋转变换相对的要复杂一些。首先我们要确定我们的坐标系是左手坐标系还是右手坐标系,这会影响到 x,y,z 三个轴的相对关系,**本文我们使用右手坐标系**来进行相关的运算。右手坐标系如下图,右手四指弯曲的方向代表 x 轴到 y 轴的方向,大拇指方向代表 z 轴方向。  我们先来看看在三维空间中绕 x,y,z 三个轴中的某个轴逆时针旋转 θ 角度的矩阵。 绕 x 轴旋转,则可以看作是在 yz 平面的二维旋转,x 轴的 (1,0,0) 不变,y 轴 (0,1,0) 变为 (0,cosθ,sinθ),z 轴的(0,0,1) 变为(0,-sinθ,cosθ),因此对应的矩阵为:  绕 y 轴旋转,则可以看作是在 xz 平面的二维旋转,y 轴的 (0,1,0) 不变,x 轴 (1,0,0) 变为 (cosθ,0,-sinθ),z 轴的(0,0,1) 变为(sinθ,0,cosθ),因此对应的矩阵为:  绕 z 轴旋转,则可以看作是在 xy 平面的二维旋转,z 轴的 (0,0,1) 不变,x 轴 (1,0,0) 变为 (cosθ,sinθ,0),y 轴的(0,1,0) 变为(-sinθ,cosθ,0),因此对应的矩阵为:  ### 绕其中两个轴旋转 上面我们得到了分别绕 x,y,z 三个轴单独旋转的旋转矩阵,接下来我们来理解下下面这个表达式的含义: >  通过上一篇提到的复合变换,上面式子表达的应该是先绕 x 轴旋转,然后再绕 y 轴旋转。假设原先物体的 x 轴方向为 (1,0,0),y 轴方向为 (0,1,0),z 轴方向为 (0,0,1),我们先将其绕 x 轴逆时针旋转 α 度,即  操作。此时物体自身的 y 轴 (0,1,0) 会跟着 x 轴的旋转变为(0,cosα,sinα),记作 y' 。那么我们再做  操作时,旋转的 y 轴是原先的 y 还是 y' 呢?这是两种完全不一样的情况,如下图  垂直向上较长的那根绿线为 y ,而较短的绿线即为 y' ,我们来看看绕它们旋转的情况分别是怎样的:  答案是:再做  操作时,旋转的 y 轴就是原先的 y=(0,1,0)。因为  的旋转矩阵是根据 y=(0,1,0) 的情况计算出来了,因此使用该矩阵计算时,无论物体属于一个什么角度,计算出来的结果都是根据 y=(0,1,0) 这个轴进行逆时针旋转的结果(注:(0,0,0) 为物体的中心点)。 我们可以称 x 轴方向为 (1,0,0),y 轴方向为(0,1,0),z 轴方向为(0,0,1) 的三个轴为**世界坐标轴**,它们不根据物体的旋转而改变。而会根据物体自身的坐标轴会根据物体的旋转而改变,例如上诉中的 y' ,我们可以称之为**模型坐标轴**。(自己按照 unity 常用的说法瞎定义了,懂原理就好。) 因此上诉的两个旋转操作都是按照世界坐标轴来进行的,这种我们称之为**外旋**,表达式  ,我们可以称之为 **x-y 外旋** 操作。那么**内旋**就是使用模型坐标轴来做旋转操作咯,那么如果我想要实现先绕 x 轴旋转 α 度,在绕旋转后的模型坐标轴的 y 轴(y')旋转 β(即 **x-y 内旋** 操作),那么应该怎么计算呢? 首先,第一步是绕 x 轴旋转,此时物体还没发生旋转,因此模型坐标的 x 轴等于世界坐标的 x 轴,因此我们依旧可以使用  矩阵。接着我们要绕 y'=(0,cosα,sinα) 旋转,这里我们需要将其进行拆解(类似于前面二维空间绕空间中任意一点旋转那样,拆解成先把任意点移到原点,然后旋转,然后再把改点移回去),先把 y' 绕世界坐标的 x 轴旋转 -α 度,使其与世界坐标的 y 轴重叠,然后使用  矩阵进行旋转 β 角度,最后再绕世界坐标的 x 轴旋转 α 度,使旋转轴 y' 回到 (0,cosα,sinα) 方向。 因此 x-y 内旋操作即为: 1. 绕世界坐标 x 轴旋转 α 度,对应矩阵  2. 绕世界坐标 x 轴旋转 -α 度,对应矩阵  3. 绕世界坐标 y 轴旋转 β 度,对应矩阵  4. 绕世界坐标 x 轴旋转 α 度,对应矩阵  可以发现第一第二步可以抵消,因此 x-y 内旋操作等价于先绕世界坐标 y 轴旋转 β 度再绕世界坐标 x 轴旋转 α 度,即 **x-y 内旋 等于 y-x 外旋**。 上诉过程用矩阵来表达的话,我们知道绕世界坐标 x 轴旋转 -α 度即为绕世界坐标 x 轴旋转 α 度的**逆变换**,因此其矩阵即为  的逆矩阵,为  ,因此矩阵如下 > x-y 内旋 =  = y-x 外旋 (  ) 同理也可得出 x-z 内旋等于 z-x 外旋,z-y 内旋等于 y-z 内旋等等。 ### 绕三个轴旋转 知道上面这些原理后,我们再进一步,来理解下面表达式 >  同样的,上面式子可以称之为 x-y-z 外旋 操作,即先绕世界坐标的 x 轴旋转 α 度,然后在绕世界坐标的 y 轴旋转 β 度,最后绕世界坐标的 z 轴旋转 γ 度。带入可得: >  那么它是否和前面一样 x-y-z 外旋 等于 z-y-x 内旋 呢?答案是肯定的,我们来看下推导。 z-y-x 内旋,重点在于如何把 z-y 操作后模型坐标 x 轴移动到世界坐标的 x 轴上,通过前面我们知道 z-y 内旋等于 y-z 外旋,因此旋转后的模型坐标 x 轴即执行了  操作,此时的模型坐标 x 轴,我们标记为 x'。因此若我们要使得 x' 变回与世界坐标的 x 重叠,只需要执行一下相反的操作即可,即把 x' 先绕 z 轴旋转 -γ 度,然后在绕 y 轴旋转 -β 度,对应矩阵为  。 因此 z-y-x 内旋可以分解为如下几步骤: 1. 先将其分解为 y-z 外旋 + x 内旋 2. 做 y-z 外旋,对应矩阵  3. 做 y-z 外旋的逆操作,使 x' 到世界坐标 x 轴上,对应矩阵  4. 绕世界坐标 x 轴旋转,对应矩阵  5. 把 x' 归位,即再做一次 y-z 外旋操作,对应矩阵  连起来可得公式为: > z-y-x 内旋 =  = x-y-z 外旋 注:  **可得结论:所有外旋操作等于与其操作顺序相反的内旋操作。** ### 排列组合 我们一共可以得到以下六种排列组合。不同的组合得到值是不一样的,因为通过矩阵的乘法,我们知道  等。 * x-y-z 外旋(等价于 z-y-x 内旋) * x-z-y 外旋(等价于 y-z-x 内旋) * y-x-z 外旋(等价于 z-x-y 内旋) * y-z-x 外旋(等价于 x-z-y 内旋) * z-x-y 外旋(等价于 y-x-z 内旋) * z-y-x 外旋(等价于 x-y-z 内旋) 上面的这些旋转方式也就是我们常用的**欧拉角旋转**。 对于上面这些排列组合,很多会解释为每个轴对应的**层级关系**,例如 x-y-z 外旋,转动 x 后,y 和 z 在之后的计算用的还是世界坐标轴,就好像 x 的转动和 yz 没有关系。y 和 z 之间也是一样,转动 y 后,z 还是用世界坐标轴计算,不会因为 y 的改变而改变。这个就很像所谓的层级关系,**即 z 为最父层,x 为最子层,y 在中间层**,当子层转动的时候,不会影响到父层。反过来也一样,x-y-z 外旋等于 z-y-x 内旋,父层的 z 转动会影响 y 和 x(内旋用的模型坐标轴)。 欧拉角的维基百科:[https://en.wikipedia.org/wiki/Euler_angles](https://en.wikipedia.org/wiki/Euler_angles) ### 万向锁(Gimbal Lock) 关于万向锁是什么,看这个视频应该就可以明白了:[https://v.youku.com/v_show/id_XNzkyOTIyMTI=.html](https://v.youku.com/v_show/id_XNzkyOTIyMTI=.html) 简单来说上诉六个组合的操作,只要把中间那个操作的旋转角度设为 90 度的整数倍,就会触发万向锁。 我们可以从内旋的角度很好理解,以 z-y-x 的内旋为例子,当我们做第一步操作时,即绕模型坐标的 z 轴旋转 α 度,无论怎么旋转,z 轴都不会改变且等于世界坐标的 z 轴,但是模型坐标的 x,y 轴会跟着旋转变换。此时我们再做第二步操作,即绕模型坐标的 y 轴逆时针旋转 β 度,当 β = 90° 时,我们会发现**此时模型坐标的 x 轴会和世界坐标的 z 轴处于同一条直线,**方向相反。那么当我们再做第三步操作时,即绕 x 轴旋转,那就等于在绕世界坐标的 z 轴旋转,就等同于第一步操作,只不过方向相反。**这就是万向锁了,即欧拉角有两个角的旋转都在绕同一个轴在旋转**。 接着我们来从数学的角度分析一下:假设我们使用 x-y-z 外旋,对应的矩阵即为 ,可得到: >  此时我们把 β 的值设为 90,可得下面矩阵:  即:  最终得到: >  即无论我们的 α 和 γ 取何值,  永远等于  。 **总结:每个内旋组合,将第二个轴的旋转角度设为 90 度或其整数倍时,就会触发万向锁,此时无论第一个轴或第三个轴的旋转角度为多少,都是在绕第一个轴所对应的世界坐标轴做旋转,从而失去了一个方向(第三个轴)的旋转能力。** ### 绕 xyz 平面中的任意轴旋转 前面我们说提到的是欧拉角旋转,即绕 x,y,z 轴旋转,若我们想要计算绕 xy 平面,或者 yz 平面,xz 平面中的任意轴(比如 (0,1,1))旋转,应该如何计算呢? 举个简单例子,假如有个轴,它在 xy 平面上,并且经过原点,那么绕该轴做逆时针旋转 θ 度应该如何来解?首先因为这个轴在 xy 平面且经过原点,因此通过绕 z 轴旋转某个角度(设 α 度)即可将该轴转到原 y 轴的方向上,然后绕该轴的逆时针旋转即是原先绕 y 轴逆时针旋转,旋转完成后再绕 z 轴旋转 -α 度即可。这点和我们前面讲欧拉角旋转时是一样的,使用公式表达即为: >  合并得 >  上诉矩阵即为三维空间中,绕 xy 平面上过原点的任意轴逆时针旋转 θ 度的矩阵,其中 α 为该轴与 y 轴的夹角。 当然了,我们一般会给定的是一个轴 (x,y,z) 这样,而不会专门告诉你夹角多少,也就是说我们要把上面矩阵的 α 给他优化掉。那么假设在 xy 平面上的某个轴为(x,y,0),那么绕这个轴旋转 θ 度的矩阵应该是多少呢? 同样的,我们设 (x,y,0) 与 y 轴的夹角为 α 度,那么可得:  与  ,看着很麻烦是不是,但是如果我们的 (x,y,0) 是**单位向量**呢?那么  ,即 sinα=x,cosα=y,所以我们**第一步先把给定的轴的向量转换为单位向量**。 接着我们将它们带入到上面的矩阵中可得:  再根据矩阵的加法定则,把 sinθ,cosθ,和常量 来个质壁分离,可得:  再根据矩阵和常数的乘法,我们可以把 sinθ和 cosθ提取出来,可得到:  因为前面说过,旋转轴转为了单位向量,所以:  和  ,进一步的简化为:  可以发现,上面中间的那个矩阵,和最左边的那个矩阵很相似,其实就是单位矩阵减去左边的那个矩阵:  换下位置可以得到:  单位矩阵我们标记为  ,而  其实就是 向量  和其转置  的积(该例子中,z=0):  **结论:若我们要绕 xy 平面上的某个轴 A=(x,y,0) 旋转 θ 度(其中 A 为单位向量),其公式为:** >  前面我们是把 xy 平面的轴转到 y 上,当然我们也可以转到 x 上,然后使用 x 的旋转,得到最终结果是一样的。举一反三也可以计算绕 xz 平面或 yz 平面的轴旋转,不过也不用举了,下面我们直接来看绕 xyz 空间中的轴旋转的公式。 ### 绕空间中过原点的轴旋转 前面我们是绕 (x,y,0)旋转,最终我们想要的肯定是绕 (x,y,z) 的旋转公式,那么绕过原点的一个轴 A=(x,y,z) 旋转 θ 度(其中 A 为单位向量),其公式应该是什么? 其实原理都是一样的,我们要先把这个轴搞到世界坐标 y 轴(也可以是 x 或 z)上,然后执行旋转操作,最后把这个轴归位。分如下几步操作: 1. 通过绕世界坐标 y 轴旋转将该轴转到 xy 平面上,其中夹角 β 为该轴在 xz 平面上的投影 (x,0,z) 与 x 轴 (1,0,0) 的夹角。 2. 通过绕世界坐标 z 轴旋转将该轴转到 y 轴上,其中夹角 α 为该轴 (x,y,z) 与 y 轴 (0,1,0) 的夹角。(因为第一步操作时,我们的旋转轴 A 与 y 轴的夹角不会发生变换) 3. 绕世界坐标 y 轴旋转 θ 度 4. 2 操作的逆操作 5. 1 操作的逆操作 可以得到如下公式: >  因为夹角 α 的对边即为 旋转轴 A 在 xz 平面上的投影,其长度即为  根据三角函数可以得到如下几个公式:     为了方便,我们设  ,  ,(即 m*n=1),将它们带入上面矩阵,得到:  进一步得到:  因为 m*n =1 所有再简化为:  全部相乘可得:  把 sinθ, cosθ,和常量拆分出来分别可得: 常量为:  就是我们  的值 cosθ 为:  该矩阵我们来一项一项的看,第一项带入 n 值得到:  ,我们来对它进行简化,如下:  所以:  第三项带入 n 值得到:  第五项带入 m 值得到:  第七项等价于第三项。 最后一项带入 n 值得到:  ,和第一项的解法类似,最终得到:  所以简化后的矩阵为:  sinθ 为:  其中由于  提取 sinθ,可得:  **结论:若我们要绕 xy 平面上的某个轴 A=(x,y,z) 逆时针旋转 θ 度(其中 A 为单位向量),其公式为:** >  若 z=0,就是我们上面在 xy 平面上的轴旋转,同理 y=0 就是在 xz 平面上的轴旋转,x=0 就是 yz 平面上的轴旋转。 ### 绕空间中不过原点的轴旋转 前面我们的轴都是规定是过原点的,若我们想要绕不过原点的某个轴旋转,其实一样的思路,先把这个轴使用**平移变换**移动到原点处,然后做上面的操作,最后把这个轴移回去即可。因为是平移操作,使用矩阵时要使用齐次坐标的矩阵,推导就不多描述了,懂原理就肯定能算出来! Unity 与旋转 --------- 在 Unity 中,我们在 Inspector 界面中设置 Transform 的 **Rotation** 属性,或者在代码里设置 **transform.localEulerAngles** ,这两种方法都是使用的欧拉角旋转。 此外我们还要注意,**Unity 使用的是左手坐标系**而非前面我们一直所举例用的右手坐标系。 左手坐标系:  面我们提到欧拉角旋转有 6 中排列组合,那么 Unity 使用的是哪种呢?在 Transform 的 Rotate 方法中,有如下一段注释: ``` The implementation of this method applies a rotation of zAngle degrees around the z axis, xAngle degrees around the x axis, and yAngle degrees around the y axis (in that order). ``` 因此我们可以知道,**Unity 使用的是 z-x-y 外旋,也就是 y-x-z 内旋**。 如何确定是正确的呢?我们可以创建一个 Cube,然后通过按照 y-x-z 的顺序来调整值,这个是内旋的顺序,即每次旋转都是按照模型坐标来旋转的,因此每次旋转对应的模型旋转轴不会发生改变。如下:  既然是使用欧拉角旋转,那么同样会存着万向锁的问题,因为是 z-x-y 的顺序,那么我们只需要把 x 轴旋转 90 度,就可触发万向锁,如图无论怎么修改 y 和 z,都是在绕模型坐标的 x 轴或者说是世界坐标的 y 轴在旋转。  同时我们还要注意,像图中,我们是先设置好 x 轴的旋转,然后再设置 y 或者 z 的旋转,这并不代表 unity 先旋转了 x 轴,再旋转其他轴。实际上无论我们怎么先后设置 xyz 三个轴的旋转值时,**Unity 始终都是要按照 z-x-y 的顺序来从初始位置开始旋转**。这点也很好理解,因为顺序不一样的话,结果也是不一样的。 ### 绕任意轴旋转 Transform 中提供了 **Rotate** 和 **RotateAround** 两种方法用于绕任意轴旋转。 **Rotate** 有如下三个参数,第一个参数为旋转轴的向量,第二个参数为旋转角度,第三个参数决定旋转轴的起点(默认为 Space.Self 即起点为物体的中心点,否则为世界坐标的原点)。 ``` public void Rotate(Vector3 axis, float angle, [DefaultValue("Space.Self")] Space relativeTo) { if (relativeTo == Space.Self) this.RotateAroundInternal(this.transform.TransformDirection(axis), angle * ((float) Math.PI / 180f)); else this.RotateAroundInternal(axis, angle * ((float) Math.PI / 180f)); } ``` 例如我们想绕过物体中心点的方向为 (1,1,1) 的轴旋转,使用下面方法即可 ``` transform.Rotate(new Vector3(1, 1, 1), Time.deltaTime * 30); ``` 效果如下:  **** **RotateAround** 若想自定义旋转轴的起点,则使用 RotateAround 方法即可 ``` public void RotateAround(Vector3 point, Vector3 axis, float angle) ``` 第一个参数即为旋转轴的起点,需要注意的是该起点的值为世界坐标的值,而不是相对于物体中心的偏移量。 若想绕起点在世界坐标 (1,0,0) 的向量 (1,1,1) 旋转,则代码为: ``` transform.RotateAround(new Vector3(1,0,0), new Vector3(1, 1, 1), Time.deltaTime * 30); ``` 效果图如下(图中物体中心在世界坐标 (0,0,0) 上):  视图变换和投影变换矩阵的原理及推导,以及OpenGL,DirectX以及Unity的对应矩阵 Asset简介