向量运算与应用 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/362035810) 什么是向量 ----- **向量指具有大小和方向的量**,一般记做: **a** ,  ,  ,同时也可以用数对的形式表示,例如:(x, y) ,(7,8,9) **向量的矩阵**表示:   **向量的大小**,也就是向量的长度(一般称作为 模),向量 a 的模记为:  ,若  ,则  **单位向量:**即模为 1 的向量,可以记作  。一个向量的单位向量,可以通过除以它模得到,即  。 **零向量:**即模为 0 的向量,零向量的方向是任意的 **相反向量:**长度相等方向相反的向量,  的相反向量为  **平行(共线)向量:**方向相同或相反的非零向量,记作  向量运算 ---- 设  ,  ### 加法 向量的加法满足平行四边形法则和三角形法则,  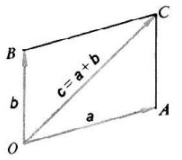 可以将其想象成一个长方形求对角线。 **运算过程:**   **一些运算律:**  交换律:  结合律:  ### 减法  ,如图 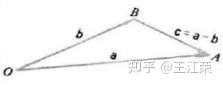 **运算过程:**   **一些运算律:**  实数和向量的积 ------- 设有实数 k,和向量  的乘积还是一个向量,记做  ,且  ,如果  ,则 k = 0 或  其几何意义为:向量的有向线段的伸长或者压缩。 **一些运算律**: 结合律:  分配律:   ### 向量的点乘(点积,内积,数量积)(Dot Product) 两个向量的数量积(点积,内积,点乘)是一个数量,没有方向,记作  **代数定义:**  **几何定义:**我们将  和  的夹角记作  ,且  若  ,  不共线,则  若  ,  共线,则  ,因为此时  则 ,若两个向量方向相反,则认为 则 。 **一些运算律:** 交换律:  结合律:  分配率:  **一些性质:**  若两个向量互相垂直,则  因此  ### 点乘的实际使用场景 1. 计算两个向量的夹角,通过点乘我们可以得到:  若  和  为单位向量,即模为 1,那么上面的式子分母即为 1,得  2. 可以用来求一个向量在另一个向量上的**投影**,例如图中  在  上的投影,我们记作  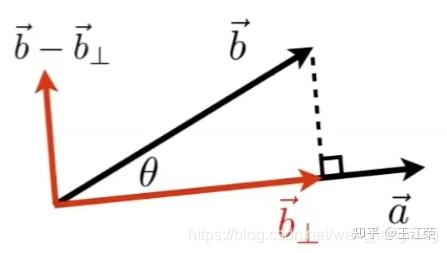 因为  是  在  上的投影,因此 的方向和  相同。因此  ,k 为一个常量, 为  的单位向量。  的值我们很好求得:  接下来要看看 k 值的含义,因为  和  方向相同, 因此  不仅是  的单位向量,同时也是  的单位向量,因此 k 即为  的模,即  然后由于  的结尾与  的结尾的连线,垂直于  (如图,也是投影的性质),因此通过三角函数,我们可以得知   的值很好求得,  我们可以通过点乘得到,因此即可求得 k 的值,然后求得  如图,通过向量的减法,我们可以得到  ,这样就把  分解成了两个互相垂直的向量。 若我们要把向量 (x, y, z) 投影到 x,y,z 的某个平面上,只需要把垂直于该平面的那个轴对应的值设置为 0 即可,例如:投影到 xy 平面,即为 (x, y, 0) ,投影到 yz 平面上,即为 (0, y, z)。若投影到某个轴上,则只保留该轴的值即可,例如:投影到 x 轴上,即为 (x, 0, 0),投影到 y 轴上,即为 (0, y, 0)。 3. 判断一个向量的朝向是否和另个向量相似,即两个向量的**方向性**,如图 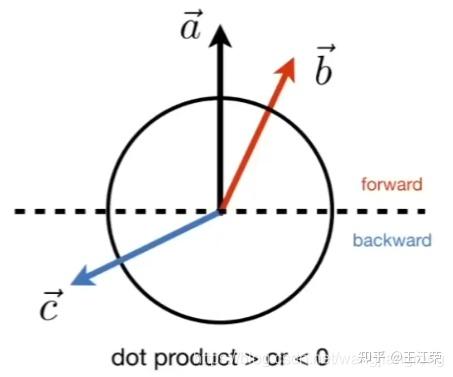 图中我们可以认为,  和  一样,同时朝向前方,而  朝向的是  的后方。我们可以通过点积的值来判断, **> 0 则为同方向(0 <= 夹角 < 90), < 0 则为反方向(90 < 夹角 <= 180), = 0 即为垂直(夹角 = 90)**。 因为  ,若两个都是非零向量,则  ,通过三角函数可知:当  ,  ,因此点积的值 > 0,当  ,  ,因此点积的值 = 0,当  ,  ,因此点积的值 < 0。 4. 两个向量是否**接近**,夹角越小,即两个向量越接近。通过上面 3 提到的,我们只能通过点积的值来判断夹角是钝角还是锐角还是直角,那么如何只通过点积的值来判断夹角大小呢?那就是我们把**两个向量的单位向量进行点积**。这样就会使  ,因此  ,那么当值为 1 时,代表两向量方向正好相同,当值越来越小时,代表两个向量离得越来越远,当值为 -1 时,代表两向量方向正好相反。因此**两个向量的单位向量的点积越接近 1,两个向量越接近**。 这个性质可以应用在**高光**的显示上,当**人眼看向目标的向量**和**光折射的向量**,它们越接近则高光效果越明显。 ### 向量的叉乘(叉积,向量积,外积)(Cross Product) 两个向量的向量积(叉积,叉乘,外积)是一个向量,记作  (或者  ) 我们将  和  的夹角记作  ,且 ,那么叉乘得到的向量的模长为:  **方向:**与这两个向量所在平面垂直,且遵守**右手螺旋定则**(四指方向代表旋转的方向,右手四指从  转向  时,大拇指的方向即向量积的方向) 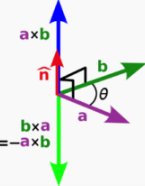 **用矩阵表示:**  若为二维向量,即 z 的值为 0,因此  ,又因为二维没有 z 轴,所以常写作  ,该常量其实就是  。 **一些运算律:**    **一些性质:**  (因为 sin0 = 0) 若两个向量互相平行,则   的值是以  和  为边的平行四边形的面积,同样的以  和  为边的三角形的面积自然就是  (至于为什么,下面第四点解释) ### 叉乘实际使用场景 1. 建立三维坐标中的坐标系,例如给定一个 x 轴和 y 轴,我们可以通过 x 轴叉积 y 轴来获得 z 轴 *  *  *  *  *  *  注:若三维坐标系的  那么该坐标系即为**右手坐标系**。 2. 判断一个向量在另一个向量的左侧还是右侧。例如我们给定两个向量  ,  ,我们想知道  在  的左侧还是右侧,该如何判定? 根据  和  的值,我们可以看出它俩都在 xy 平面上,根据叉积的性质我们可以知道  得到的向量一定垂直于 xy 平面(和 z 轴平行或重叠),然后根据右手螺旋法则,若  的向量的 z 的值 > 0 ,那么即表示  在  的右侧,若 z 的值 < 0 ,那么即表示  在  的左侧。 上面的例子我们是从 z 轴的正方向看向负方向,但是若从负方向看向正方向,那么原本在左边就会变成在右边,因此左右关系和我们的观察方向有关。 因此若我们从 z 轴正方向看向负方向,若两个向量组成的平面没有平行于 xy 平面,我们可以先将其投影到 xy 平面上,然后再计算左右。 3. 判断点是否在三角形内部。 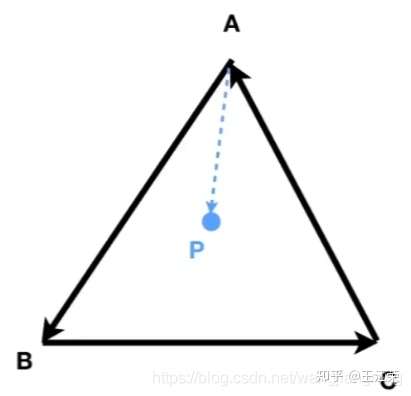 其实本质上还是 2 中的思路,例如上图,我们可以利用  ,  ,  来判断 P 点是否在  ,  ,  的左侧,若成立,则 P 点在三角形 ABC 的内部。 同理可以应用到四边形等多边形中,但是必须夹角小于 180 度(如下图,ABC>180,因此 P 点即使在内部,但是却在  的右侧,  的左侧)。 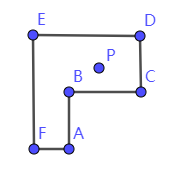 这点是**三角形光栅化**的基础,要判断三角形覆盖了哪些像素,那就需要知道这些像素是否在三角形内部,好给这个像素进行着色。 4. 求三角形面积 如下图三角形,CD 长度为 h,AC 长度为 b,AB 长度为 c,AC 和 AB 的夹角为 α 。 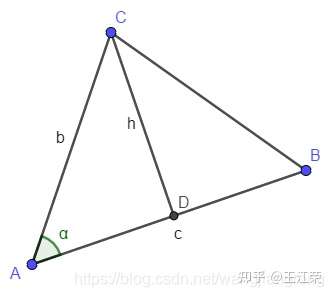 我们知道其面积为:  因为  因此  而  正是我们向量 AC 和向量 AB 叉乘结果的模  因此  直线与三角形的重心坐标(Barycentric Coordinates)的推导与应用 矩阵运算与常用矩阵