数据结构与算法——二叉平衡树(AVL树)详解 agile Posted on Jul 13 2023 数据结构与算法 ### 什么是ALV树 大家好,我是bigsai,好久不见,甚是想念。 对于树这种数据结构,想必大家也已经不再陌生,我们简单回顾一下。 在树的种类中,通常分成二叉树和多叉树,我们熟悉的二叉树种类有二叉搜索(排序、查找)树、二叉平衡树、伸展树、红黑树等等。而熟悉的多叉树像B树、字典树都是经典多叉树。 普通的二叉树,我们研究其遍历方式,因为其没啥规则约束查找和插入都很随意所以很少有研究价值。 但是二叉树结构上很有特点:左孩子和右孩子,两个不同方向的孩子对应二进制的01,判断的对错,**比较的大小** ,所以根据这个结构所有树左侧节点比父节点小,右侧节点比父节点大,这时候就诞生了二叉搜索(排序)树。二叉搜索(排序)树的一大特点就是查找效率提高了,因为查找一个元素位置或者查看元素是否存在通过每遇到一个节点直接进行比较就可以一步步逼近结果的位置。 但二叉搜索(排序树)有个很大的问题就是当插入节点很有序,很可能成为一棵斜树或者深度很高,那么这样的一个查找效率还是趋近于线性O(n)级别,所以这种情况二叉搜索(排序)树的效率是比较低的。 所以,人们有个期望:对一棵树来说插入节点,小的还在左面,大的还在右面方便查找,但是能不能不要出现那么斜的情况? 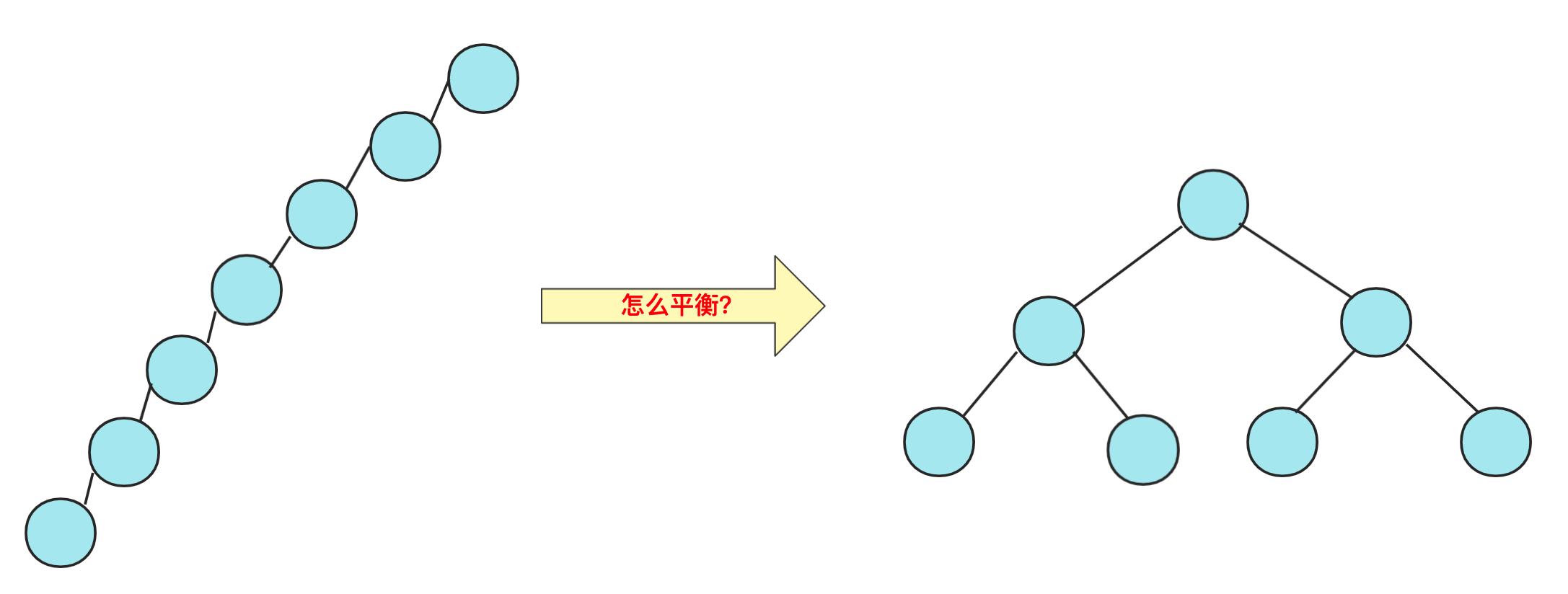 这不,平衡二叉搜索(AVL)树就是这么干的,AVL在插入的时候每次都会旋转自平衡,让整个树一直处于平衡状态,让整个树的查询更加稳定(logN)。我们首先来看一下什么是ALV树: - AVL树是**带有平衡条件的二叉搜索树**,这个平衡条件必须要容易保持,而且要保证它的深度是O(logN)。 - AVL的左右子树的高度差(平衡因子)不大于1,并且它的每个子树也都是平衡二叉树。 - 对于平衡二叉树的最小个数,`n0=0`;`n1=1`;`nk=n(k-1)+n(k-2)+1`;(求法可以类比斐波那契) 难点:AVL是一颗二叉排序树,用什么样的规则或者规律让它能够在**复杂度不太高**的情况下**实现动态平衡**呢?  ### 不平衡情况 如果从简单情况模型看,其实四种不平衡情况很简单,分别是RR,LL,RL,LR四种不平衡情况。 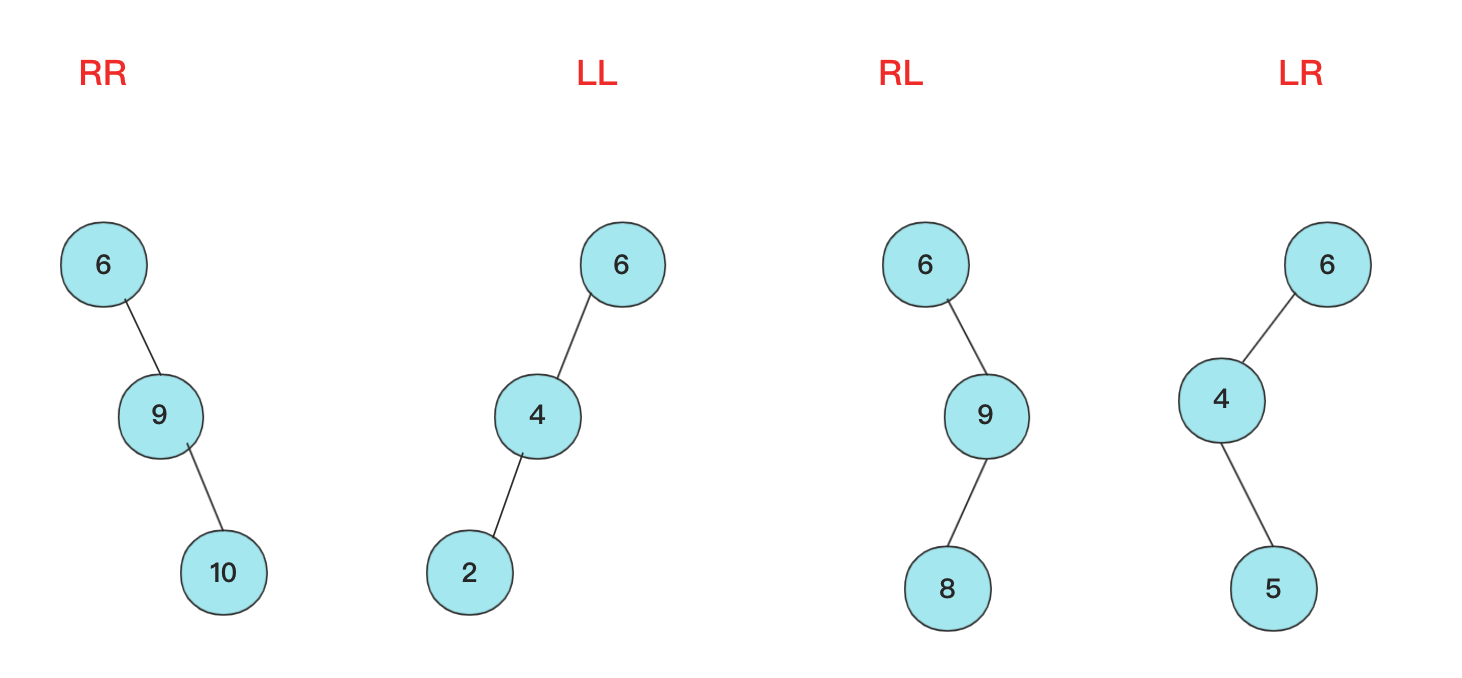 然后将其平衡的结果也很容易(不考虑其附带节点只看结果),将中间大小数值移动最上方,其他相对位置不变即可: 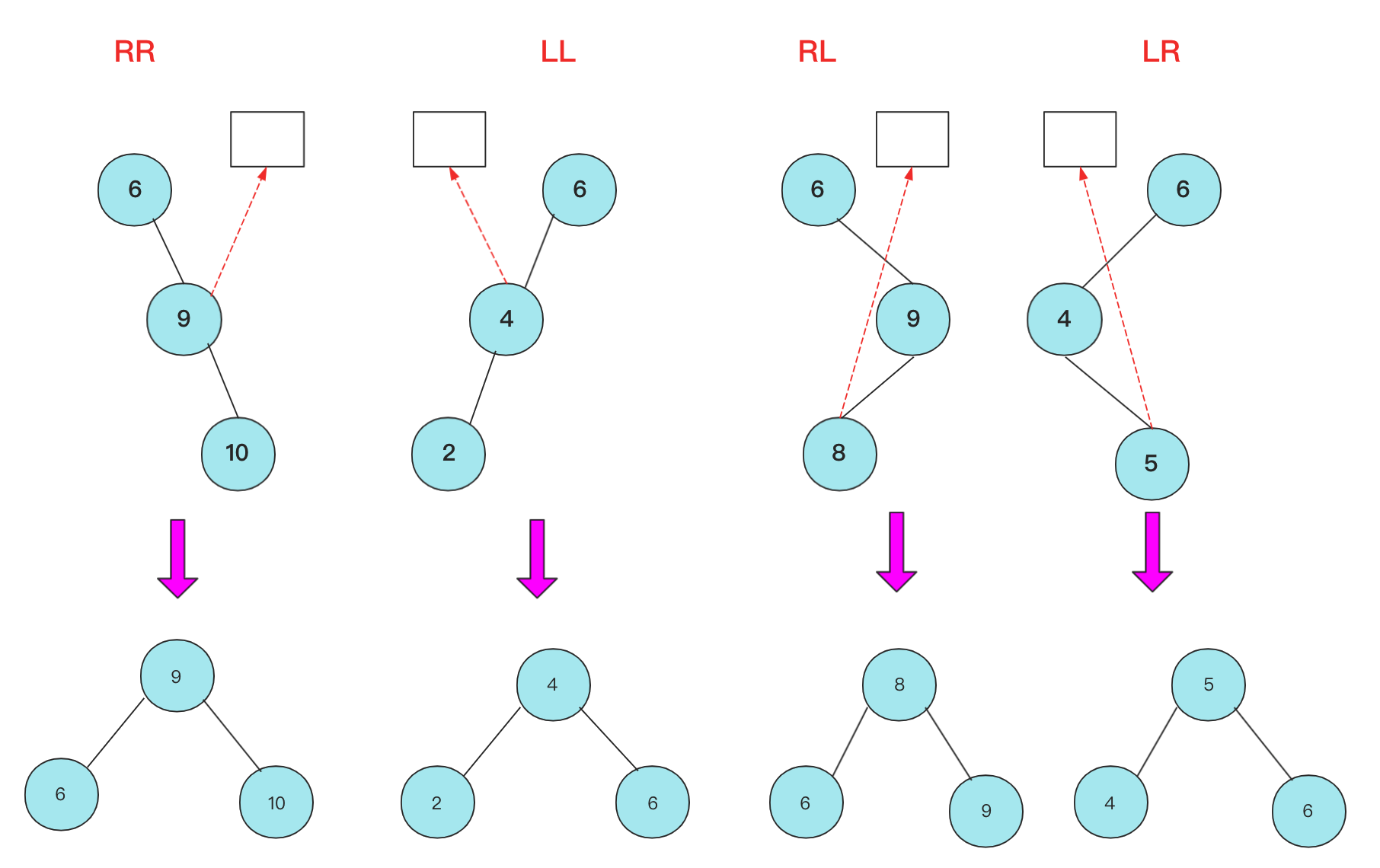 当然,这个仅仅是针对三个节点情况太过于理想化了,很多时候让你找不平衡的点,或者我们在解决不平衡的时候,我们需要的就是找到**第一个不平衡(从底往上)**的点将其平衡即可,下面列举两个不平衡的例子:  上述四种不平衡条件情况,**可能出现在底部,也可能出现在头,也可能出现在某个中间节点导致不平衡,** 而我们只需要研究其首次不平衡点,**解决之后整棵树即继续平衡**,在具体的处理上我们使用递归的方式解决问题。 ### 四种不平衡情况处理 针对四种不平衡的情况,这里对每种情况进行详细的讲解。 #### RR平衡旋转(左单旋转) 这里的RR指的是节点模型的样子,其含义是需要左单旋转(记忆时候需要注意一下RR不是右旋转)! 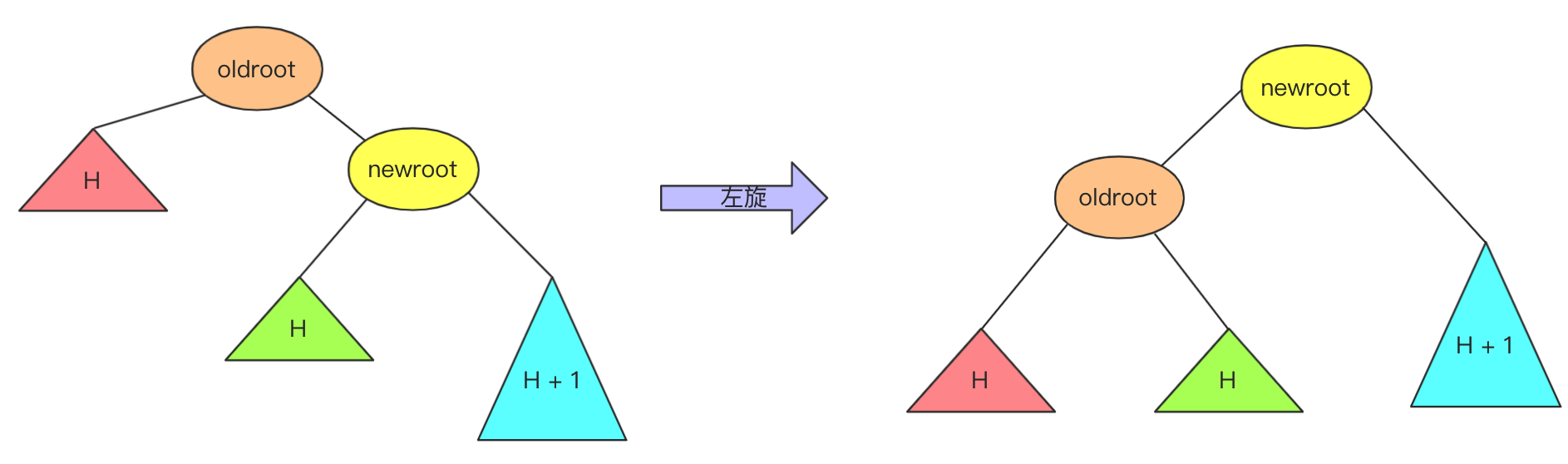 出现这种情况的原因是节点的**右侧的右侧较深**这时候不平衡节点需要左旋,再细看过程。 - 在左旋的过程中,`root(oldroot)`节点下沉,`中间节点(newroot)`上浮.而其中`中间节点(newroot)`的右侧依然不变。 - 它上浮左侧所以需要指向`根节点(oldroot)`(毕竟一棵树)。但是这样`newroot`原来左侧节点`H`空缺。而我们需要仍然让**整个树完整并且满足二叉排序树的规则**。 - 而刚好**本来oldroot右侧指向newroot**现在结构改变**oldroot**右侧空缺,刚好这个位置满足**在oldroot的右侧,在newroot的左侧,**所以我们将H插入在这个位置。 - 其中H可能为`NULL`,不过不影响操作! 其更详细流程为: 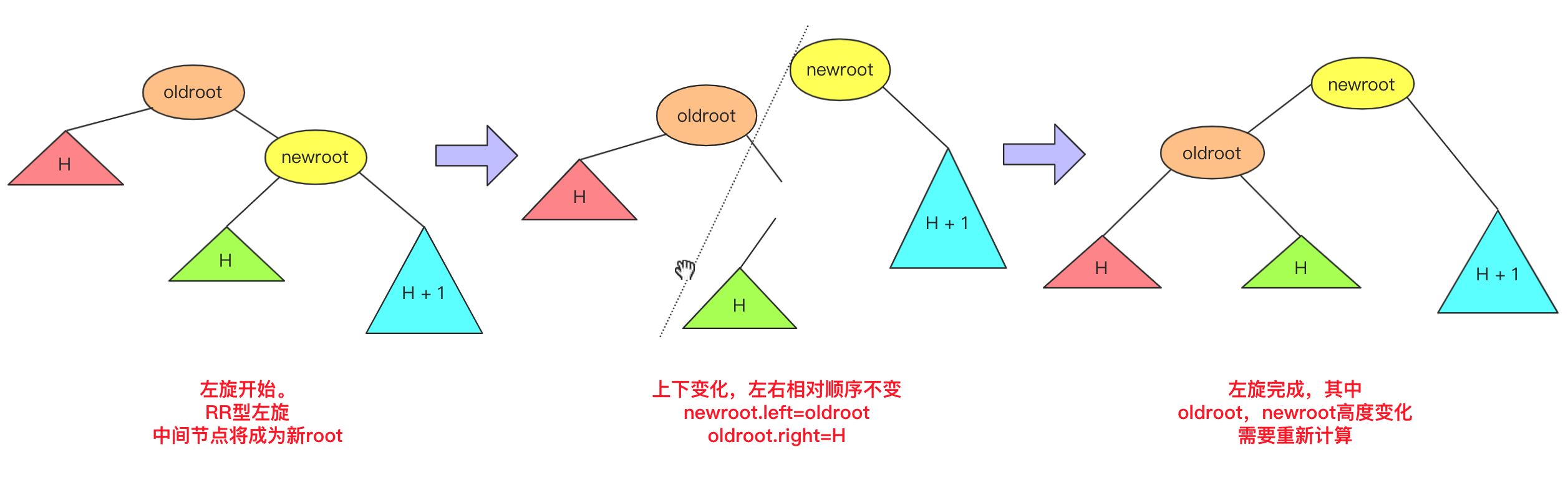 而左旋的代码可以表示为: ```java private node getRRbanlance(node oldroot) {//右右深,需要左旋 // TODO Auto-generated method stub node newroot=oldroot.right; oldroot.right=newroot.left; newroot.left=oldroot; oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1; newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新计算 return newroot; } ``` #### LL平衡旋转(右单旋转) 而右旋和左旋相反,但是思路相同,根据上述进行替换即可! 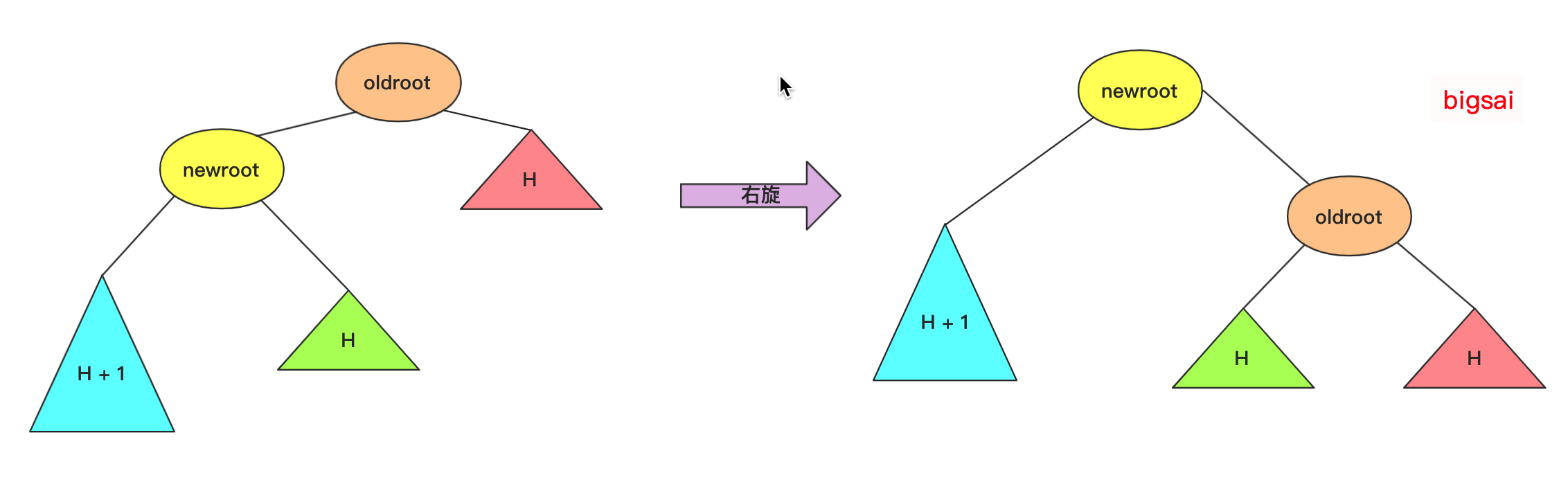 代码: ```java private node getLLbanlance(node oldroot) {//LL小,需要右旋转 // TODO Auto-generated method stub node newroot=oldroot.left; oldroot.left=newroot.right; newroot.right=oldroot; oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1; newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新金酸 return newroot; } ``` #### RL平衡旋转(先右后左双旋转) 这个RL你可能有点懵圈,为啥RR叫左旋,LL叫右旋,这个RL怎么就叫先右后左旋转了? 别急别急,这个之所以先后后左,是因为具体需要中间节点右旋一次,然后上面节点左旋一次才能平衡,具体可以下面慢慢看。 首先产生这种不平衡的条件原因是:ROOT节点右侧左侧节点的深度高些,使得与左侧的差大于1,这个与我们前面看到的左旋右旋不同因为旋转一次无法达到平衡! 对于右左结构,**中间(R)的最大,两侧(ROOT,R.L)的最小**,但是下面(`R.L`)的比上面(`ROOT`)大(`R.L`在`ROOT`右侧)所以如果平衡的话,那么`R.L`应该在中间,而`R`应该在右侧,原来的`ROOT`在左侧。 这个过程节点的变化浮动比较大,需要**妥善处理各个子节点的移动**使其满足**二叉排序树的**性质! 这种双旋转具体实现其实也不难,不要被外表唬住,这里面双旋转我提供两种解答方法。 **思路(标准答案)1:两次旋转RR,LL** 这个处理起来非常容易,因为前面已经解决RR(左旋),LL(右旋)的问题,所以这里面在上面基础上可以直接解决,首先对R节点进行一次LL右旋,旋转一次之后R在最右侧,这就转化成RR不平衡旋转的问题了,所以这个时候以ROOT开始一次RR左旋即可完成平衡,具体流程可以参考下面这张图。 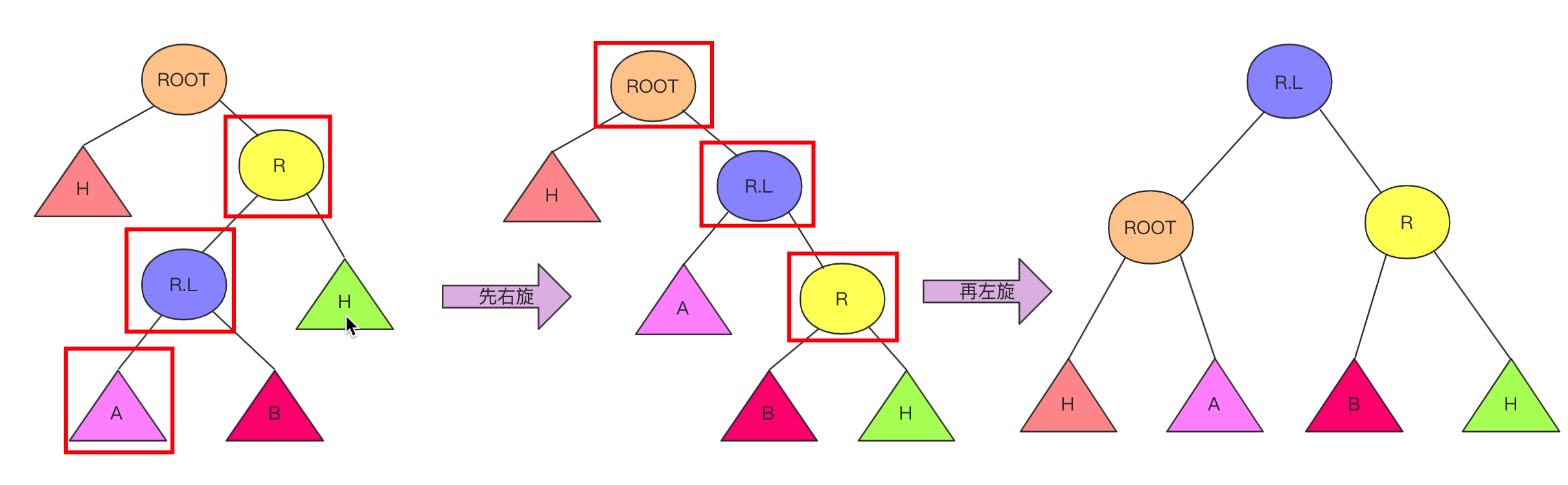 **思路(个人方法)2:直接分析** 根据初始和结果的状态,然后分析各个节点变化顺序=,手动操作这些节点即可。其实不管你怎么操作,只要能满足**最后结构一致**就行啦! 首先根据`ROOT`,`R`,`R.L`三个节点变化,`R.L`肯定要在最顶层,左右分别指向ROOT和R,那么这其中`R.left`,`ROOT.right`发生变化(原来分别是R.L和R)暂时为空。而刚好根据**左右大小关系**可以补上`R.L`原来的孩子节点`A`,`B`。 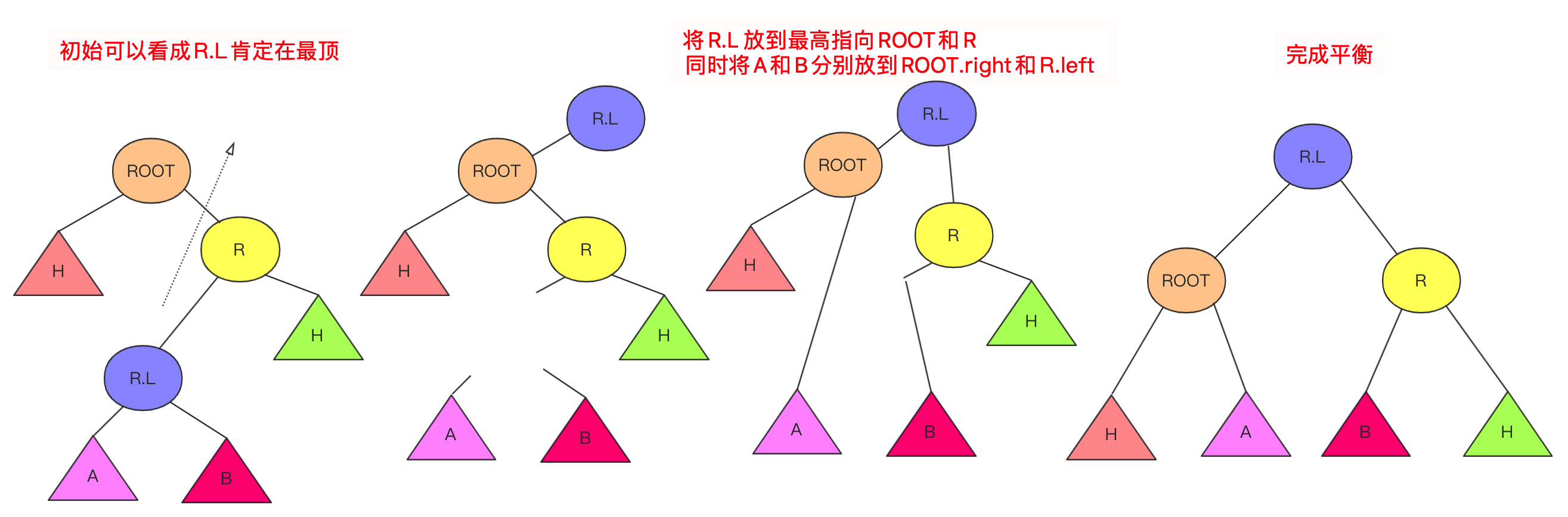 代码为:(注释部分为方案1) ```java private node getRLbanlance(node oldroot) {//右左深 // node newroot=oldroot.right.left; // oldroot.right.left=newroot.right; // newroot.right=oldroot.right; // oldroot.right=newroot.left; // newroot.left=oldroot; // oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1; // newroot.right.height=Math.max(getHeight(newroot.right.left),getHeight(newroot.right.right))+1; // newroot.height=Math.max(getHeight(oldroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新金酸 oldroot.right =getLLbanlance(oldroot.right); oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1; return getRRbanlance(oldroot); } ``` #### LR平衡旋转(先左后右双旋转) 这个情况和RL情况相似,采取相同操作即可。 根据上述RL修改即可 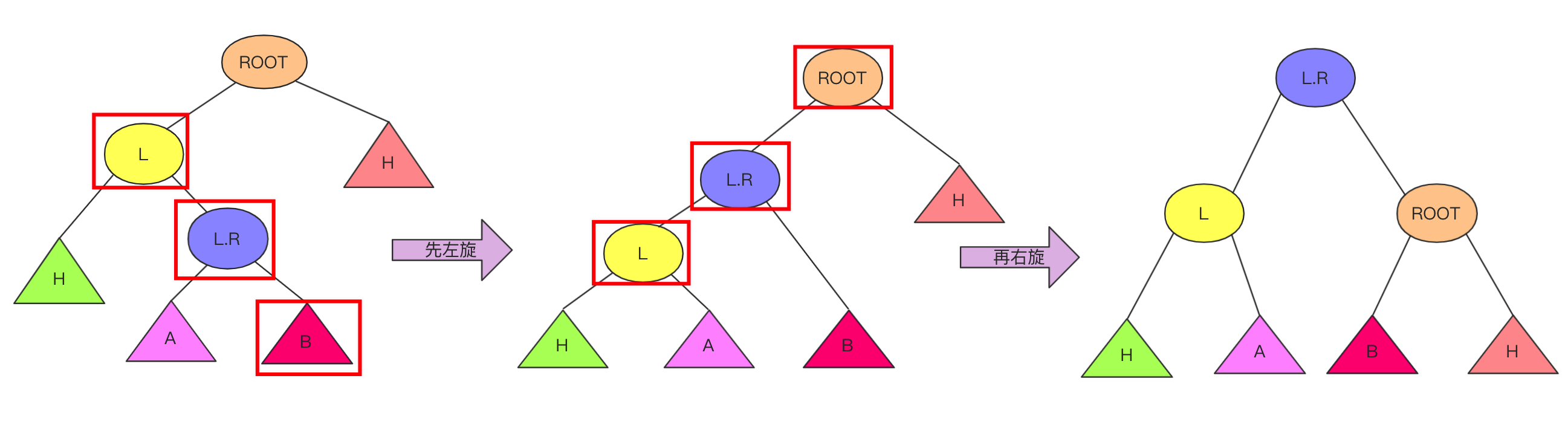 ```java private node getLRbanlance(node oldroot) { oldroot.left =getRRbanlance(oldroot.left); oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1; return getLLbanlance(oldroot); } ``` ### 代码实现 首先对于节点多个`height`属性。用于计算高度(平衡因子) 插入是**递归插入**,递归是一个来回的过程,去的过程进行插入,**回的过程进行高度更新,和检查是否平衡。**推荐不要写全局递归计算高度,效率太低下,事实上高度变化只和插入和平衡有关,仔细考虑即不会有疏漏! 代码写的比较早,如有命名不规范的情况,还请勿喷,如果有疏漏还请指出! ```java import java.util.ArrayDeque; import java.util.Queue; public class AVLTree { class node { int value; node left; node right; int height; public node() { } public node(int value) { this.value=value; this.height=0; } public node(int value,node left,node right) { this.value=value; this.left=left;this.right=right; this.height=0; } } node root;// 根 public AVLTree() { this.root = null; } public boolean isContains(int x)// 是否存在 { node current = root; if (root == null) { return false; } while (current.value != x && current != null) { if (x < current.value) { current = current.left; } if (x > current.value) { current = current.right; } if (current == null) { return false; } // 在里面判断如果超直接返回 } // 如果在这个位置判断是否为空会导致current.value不存在报错 if (current.value == x) { return true; } return false; } public int getHeight(node t) { if(t==null) {return -1;}// return t.height; //return 1+Math.max(getHeight(t.left), getHeight(t.right));这种效率太低 } public void cengxu(node t) {//层序遍历 Queue<node> q1 = new ArrayDeque<node>(); if (t == null) return; if (t != null) { q1.add(t); } while (!q1.isEmpty()) { node t1 = q1.poll(); if (t1.left != null) q1.add(t1.left); if (t1.right != null) q1.add(t1.right); System.out.print(t1.value + " "); } System.out.println(); } public void zhongxu(node t)//中序遍历 中序遍历:左子树---> 根结点 ---> 右子树 {//为了测试改成中后都行 if(t!=null) { zhongxu(t.left); System.out.print(t.value+" ");//访问完左节点访问当前节点 zhongxu(t.right); //System.out.print(t.value+" ");//访问完左节点访问当前节点 } } public void qianxu(node t)//前序递归 前序遍历:根结点 ---> 左子树 ---> 右子树 { if(t!=null) { System.out.print(t.value+" ");//当前节点 qianxu(t.left ); qianxu(t.right);} } public void insert(int value) { root=insert(value, root); } public node insert(int x,node t)//插入 t是root的引用 { node a1=new node(x); //if(root==null) {root=a1;return root;} if(t==null) {return a1;} //插入操作。递归实现 else if(t!=null) { if(x<t.value) { t.left=insert(x,t.left);} else { t.right= insert(x,t.right);} } /* * 更新当前节点的高度,因为整个插入只有被插入的一方有影响, * 所以递归会更新好最底层的,上层可直接调用 */ t.height=Math.max(getHeight(t.left),getHeight(t.right))+1;//不要写成递归, 递归效率低 return banlance(t);//因为java对象传参机制,需要克隆,不可直接t=xx 否则变换 } private node banlance(node t) { // TODO Auto-generated method stub //if(t==null)return null; int lefthigh=getHeight(t.left); int righthigh=getHeight(t.right); if(Math.abs(lefthigh-righthigh)<=1)//不需要平衡滴 { return t;} else if(lefthigh<righthigh)//右侧大 { if(getHeight(t.right.left)<getHeight(t.right.right))//RR需要左旋 { return getRRbanlance(t); } else { return getRLbanlance(t); } } else { if(getHeight(t.left.left)>getHeight(t.left.right))//ll 左左 { return getLLbanlance(t); } else { return getLRbanlance(t); } } } /* * oldroot(平衡因子为2,不平衡) ==> newroot * / \ / \ * B newroot(平衡因子为1) oldroot D * / \ / \ \ * C D B C E * \ * E */ private node getRRbanlance(node oldroot) {//右右深,需要左旋 // TODO Auto-generated method stub node newroot=oldroot.right; oldroot.right=newroot.left; newroot.left=oldroot; oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1; newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新计算 return newroot; } /* * 右旋同理 */ private node getLLbanlance(node oldroot) {//LL小,需要右旋转 // TODO Auto-generated method stub node newroot=oldroot.left; oldroot.left=newroot.right; newroot.right=oldroot; oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1; newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新金酸 return newroot; } private node getLRbanlance(node oldroot) { oldroot.left =getRRbanlance(oldroot.left); oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1; return getLLbanlance(oldroot); } /* (不平衡出现在右左节点) * oldroot ==> newroot * / \ / \ * A B oldroot B * / \ / \ / \ * newroot D A E F D * / \ * E F */ private node getRLbanlance(node oldroot) {//右左深 // node newroot=oldroot.right.left; // oldroot.right.left=newroot.right; // newroot.right=oldroot.right; // oldroot.right=newroot.left; // newroot.left=oldroot; // oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1; // newroot.right.height=Math.max(getHeight(newroot.right.left),getHeight(newroot.right.right))+1; // newroot.height=Math.max(getHeight(oldroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新金酸 oldroot.right =getLLbanlance(oldroot.right); oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1; return getRRbanlance(oldroot); } } ``` 测试情况: 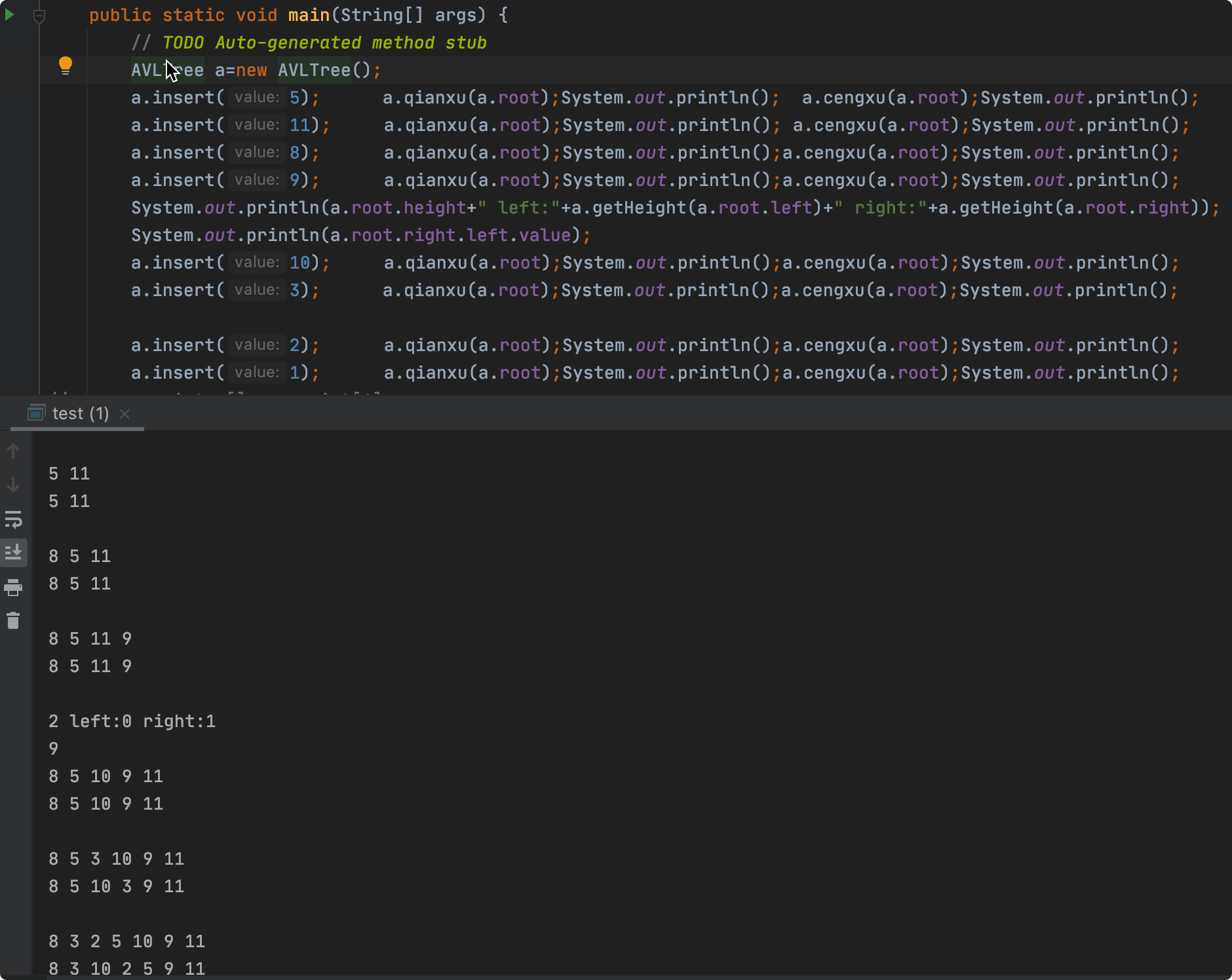 AVL的理解需要时间,当然笔者的AVL自己写的可能有些疏漏,如果有问题还请各位一起探讨! 当然,除了插入,AVL还有删除等其他操作,(原理相似。删除后平衡)有兴趣可以一起研究。 浅谈迷宫搜索类的双向bfs问题(例题解析) 数据结构与算法——前导