数据结构与算法—哈夫曼树详解与构造 agile Posted on Jul 13 2023 数据结构与算法 ### 哈夫曼树介绍 hello,大家好,我是bigsai。 哈夫曼树、哈夫曼编码很多人可能听过,但是可能并没有认真学习了解,今天这篇就比较详细的讲一下哈夫曼树。 首先哈夫曼树是什么? 哈夫曼树的**定义**:给定N个权值作为N个叶子结点,构造一棵二叉树,**若该树的带权路径长度达到最小**,称这样的二叉树为**最优二叉树**,也称为哈夫曼树(Huffman Tree),哈夫曼树是带权路径长度最短的树。权值较大的结点离根较近。 那这个树长啥样子呢?例如开始**2,3,6,8,9**权值节点构成的哈夫曼树是这样的: 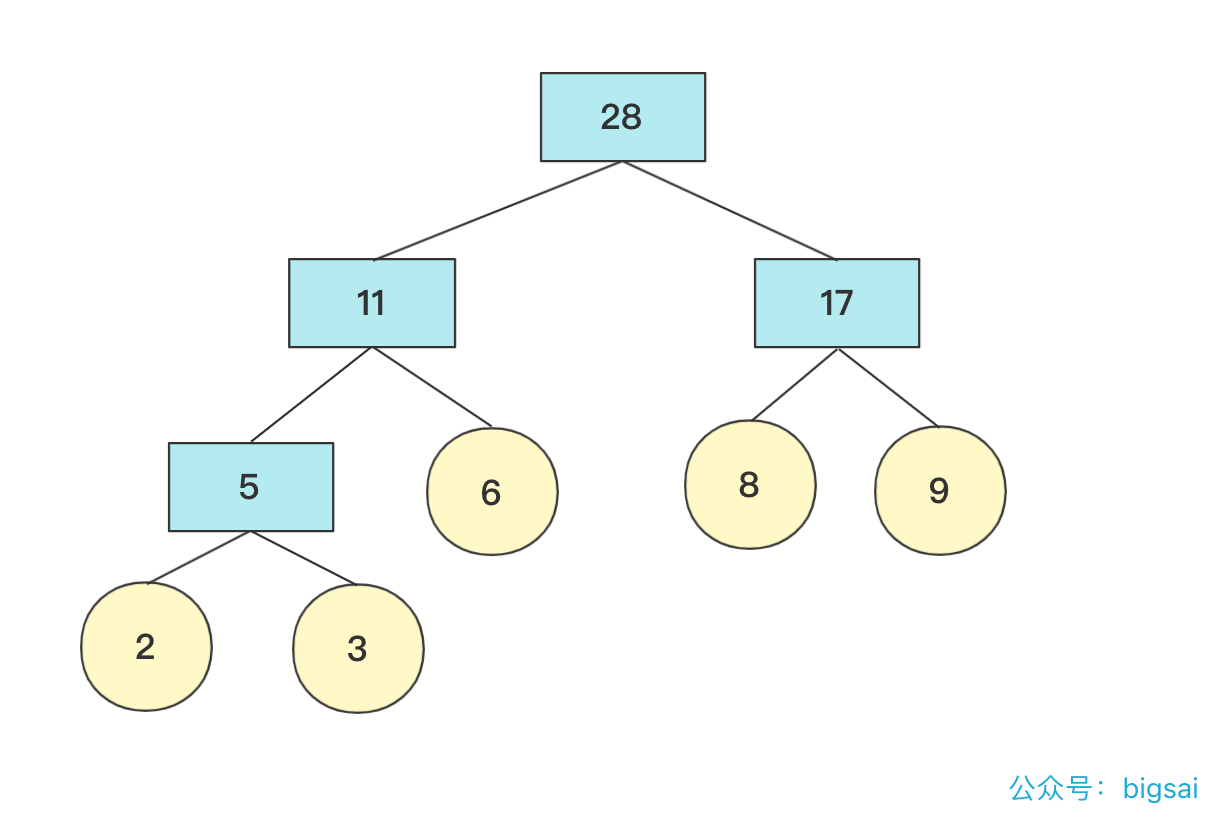 从定义和图上你也可以发现下面的规律: - 初始节点都在树的叶子节点上 - 权值大的节点离根更近 - 每个非叶子节点都有两个孩子(因为我们自下向上构造,两个孩子构成一个新树的根节点) 你可能会好奇这么一个哈夫曼树是怎么构造的,其实它是按照一个**贪心思想**和规则构造,而构造出来的这个树的权值最小。这个规则下面会具体讲解。 哈夫曼树非常重要的一点:`WPL`(树的所有**叶结点**的带权路径长度之和)。至于为什么按照哈夫曼树方法构造得到的权重最小,这里不进行证明,但是你从局部来看(三个节点)也要权值大的在上一层WPL才更低。 **WPL计算方法**: WPL=求和(Wi * Li)其中Wi是第i个节点的权值(value)。Li是第i个节点的长(深)度. 例如上面 **2,3,6,8,9**权值节点构成的哈夫曼树的WPL计算为(设根为第0层): 比如上述哈夫曼树的`WPL`为:`2*3+3*3+6*2+8*2+9*2=(2+3)*3+(6+8+9)*2=61`. 既然了解了哈夫曼树的一些概念和WPL的计算方式,下面看看哈夫曼树的具体构造方式吧! ### 哈夫曼树构造 初始给一个森林有n个节点。我们主要使用**贪心的思想**来完成哈夫曼树的构造: 1. 在n个节点找到两个最小权值节点(根),两个为叶子结构构建一棵新树(根节点权值为左右孩子权值和) 2. 先删掉两个最小节点(n-2)个,然后加入构建的新节点(n-1)个 3. 重复上面操作,一直到所有节点都被处理 在具体实现上,找到最小两个节点需要排序操作,我们来看看**2,6,8,9,3**权值节点构成哈夫曼树的过程。 初始时候各个节点独立,先将其排序(这里使用优先队列),然后选两个最小节点(抛出)生成一个新的节点,再将其加入优先队列中,此次操作完成后优先队列中有**5,6,8,9**节点 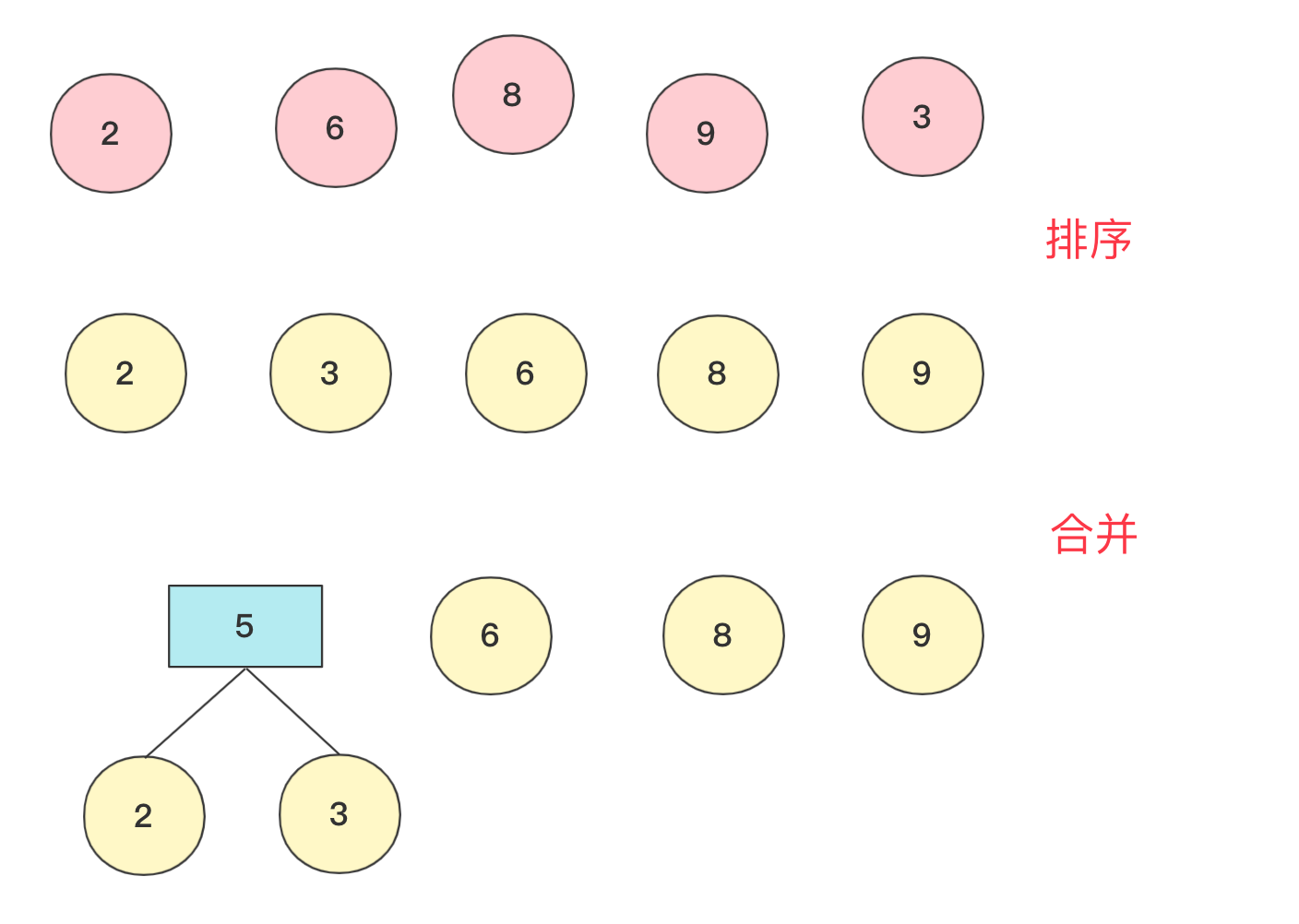 重复上面操作,这次结束 队列中有**11,8,9**节点(排序后8,9,11) 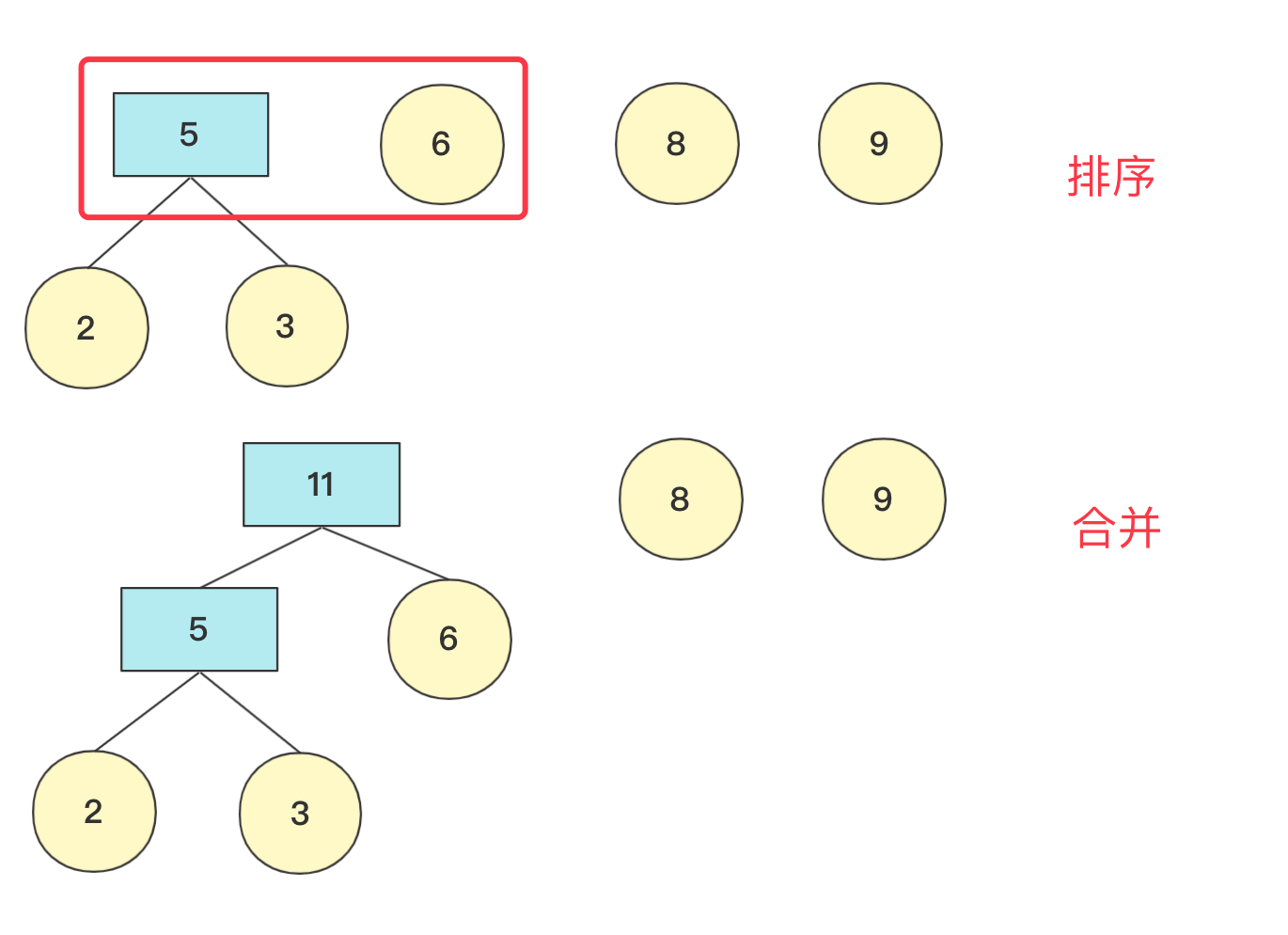 如果队列为空,那么返回节点,并且这个节点为整个哈夫曼树根节点root。 否则继续加入队列进行排序。重复上述操作,**直到队列为空**。 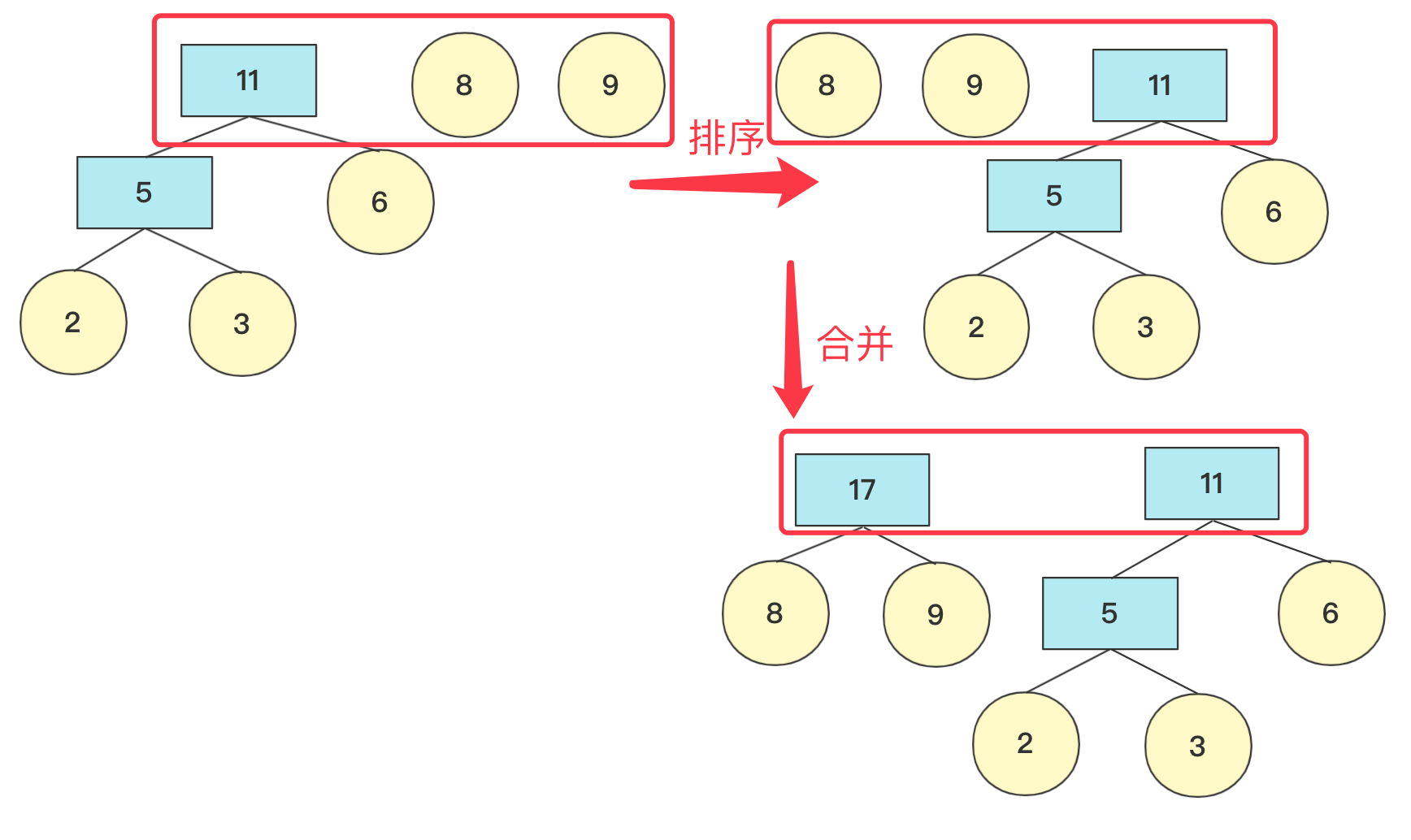 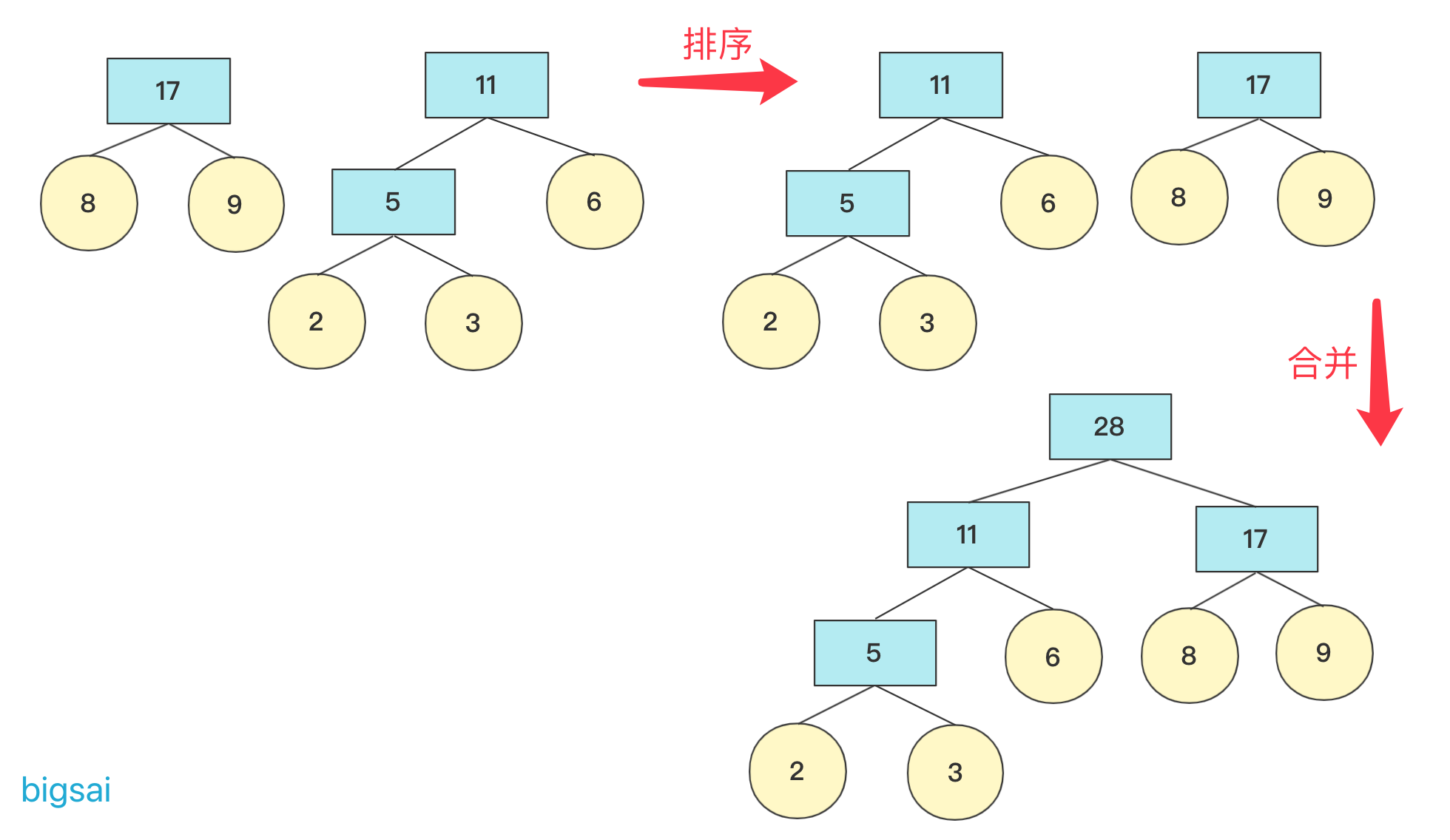 在计算带权路径长度WPL的时候,需要重新计算高度(从下往上),因为哈夫曼树是从下往上构造的,并没有以常量维护高度,可以构造好然后计算高度。 具体代码实现 ```java import java.util.ArrayDeque; import java.util.ArrayList; import java.util.Comparator; import java.util.List; import java.util.PriorityQueue; import java.util.Queue; public class HuffmanTree { public static class node { int value; node left; node right; int deep;//记录深度 public node(int value) { this.value=value; this.deep=0; } public node(node n1, node n2, int value) { this.left=n1; this.right=n2; this.value=value; } } private node root;//最后生成的根节点 List<node>nodes; public HuffmanTree() { this.nodes=null; } public HuffmanTree(List<node>nodes) { this.nodes=nodes; } public void createTree() { Queue<node>q1=new PriorityQueue<node>(new Comparator<node>() { public int compare(node o1, node o2) { return o1.value-o2.value; }}); q1.addAll(nodes); while(!q1.isEmpty()){ node n1=q1.poll(); node n2=q1.poll(); node parent=new node(n1,n2,n1.value+n2.value); if(q1.isEmpty()){ root=parent;return; } q1.add(parent); } } public int getweight() { Queue<node>q1=new ArrayDeque<node>(); q1.add(root); int weight=0; while (!q1.isEmpty()) { node va=q1.poll(); if(va.left!=null){ va.left.deep=va.deep+1;va.right.deep=va.deep+1; q1.add(va.left);q1.add(va.right); } else { weight+=va.deep*va.value; } } return weight; } public static void main(String[] args) { List<node>list=new ArrayList<node>(); list.add(new node(2)); list.add(new node(3)); list.add(new node(6)); list.add(new node(8));list.add(new node(9)); HuffmanTree tree=new HuffmanTree(); tree.nodes=list; tree.createTree(); System.out.println(tree.getweight()); } } ``` 输出结果: > 61 ### 哈夫曼编码 除了哈夫曼树你听过,哈夫曼编码你可能也听过,但是不一定了解它是个什么玩意儿,哈夫曼编码其实就是哈夫曼树的一个非常重要的应用,在这里就简单介绍原理并不详细实现了。 哈夫曼编码定义:**哈夫曼**编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据**字符出现概率**来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。 哈夫曼编码的目的是为了减少存储体积,以一个连续的字符串为例,抛开编程语言中实际存储,就拿 `aaaaaaaaaabbbbbcccdde` 这个字符串来说,在计算机中如果每个字符都是定长存储(假设长为4的二进制存储),计算机只知道0和1的二进制,假设 > a:0001 > > b:0010 > > c:0011 > > d:0100 > > e:0101 那么上面字符串可以用二进制存储是这样的 `000100010001000100010001……0101` **如果每个字符编码等长**,那么就没有空间优化可言,都是单个字符长度 * 字符个数。但是如**果每个字符编码不等长**,那么设计的开放性就很强了。 比如一个字符串`aaaaabb` 如果设计`a`为01,`b`设计为1。那么二进制就为:`010101010111` 如果设计`a`为1,`b`设计为01。那么二进制就为:`111110101` 如果设计`a`为1,`b`设计为0。那么二进制就为:`1111100` 你看,在计算机的01二进制世界中,明显第二种比第一种优先,第三种又比第二种优先。所以,**设计编码要考虑让出现多的尽量更短,出现少的稍微长点没关系**。 但是,你需要考虑的一个问题是,二进制开始**0,1,01,10,11**这个顺序 ,如果来了**001**它到底是**0,0,1还是0,01**呢?所以编码不等长的时候你要考虑到这个编码要有**唯一性不能出现歧义**。这个怎么搞呢? 简单啊,计算机只知道01二进制,而二叉树刚好有左右两个节点,至于一个字符它如果是对应叶子节点,那么就可以直接确定,也就是这个数值如果映射成一个二叉树字符不能存在非叶子节点上。 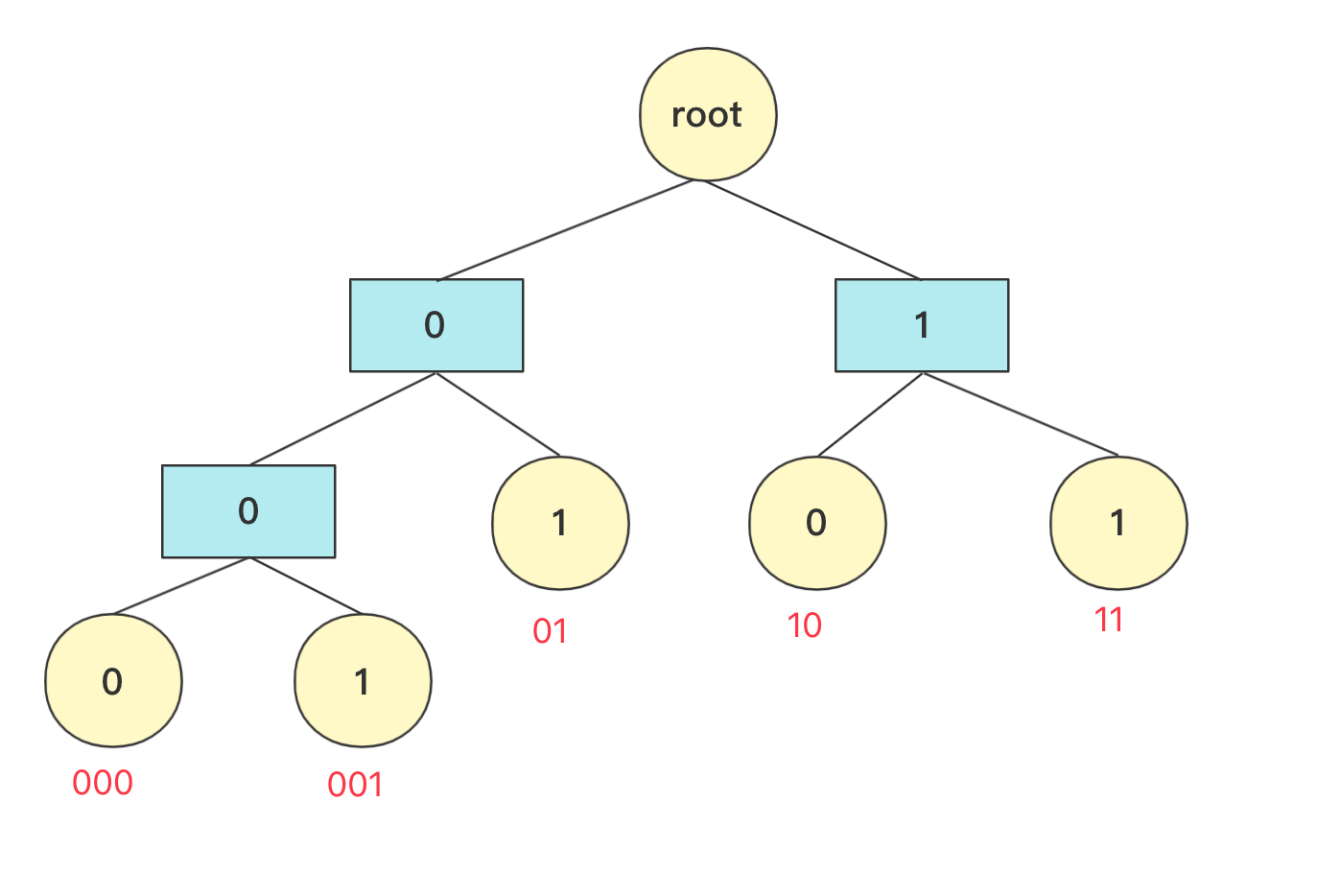 所以,哈夫曼编码具体流程就很清晰了,先统计字符出现的次数,然后将这个次数当成权值按照上面介绍的方法构造一棵哈夫曼树,然后树的根不存,往左为0往右为1每个叶子节点得到的二进制数字就是它的编码,这样频率高的字符在上面更短在整个二进制存储中也更节省空间。 ### 结语 哈夫曼树还是比较容易理解,主要构造利用贪心算法的思想去从下往上构建,哈夫曼编码相信看了你也有所收获,有兴趣可以自己实现一下哈夫曼编码的代码(编码、解码)。本人水平有限,如果有错误还希望大佬指正! 数据结构与算法—二叉树前序中序后序(递归、非递归)遍历 数据结构与算法—全排列系列