数据结构与算法知识树整理——数据结构篇——线性结构 agile Posted on Jun 18 2023 数据结构与算法知识树整理 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [www.cnblogs.com](https://www.cnblogs.com/moran-amos/p/14420676.html) 数据结构知识树整理 ========= 线性结构 ---- ### 数组 * 数组(Array)是一种**线性表**数据结构。它用一组**连续的内存空间**,来存储一组具有**相同类型**的数据。 * 线性表(Linear List)。顾名思义,线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组,链表、队列、栈等也是线性表结构。而与它相对立的概念是非线性表,比如二叉树、堆、图等。之所以叫非线性,是因为,在非线性表中,数据之间并不是简单的前后关系。 * 连续的内存空间和相同类型的数据。正是因为这两个限制,它才有了一个堪称 “杀手锏” 的特性:“随机访问”。但有利就有弊,这两个限制也让数组的很多操作变得非常低效,比如要想在数组中删除、插入一个数据,为了保证连续性,就需要做大量的数据搬移工作。 * 这里我要特别纠正一个 “错误”。我在面试的时候,常常会问数组和链表的区别,很多人都回答说,“链表适合插入、删除,时间复杂度 O(1);数组适合查找,查找时间复杂度为 O(1)”。实际上,这种表述是不准确的。数组是适合查找操作,但是查找的时间复杂度并不为 O(1)。即便是排好序的数组,你用二分查找,时间复杂度也是 O(logn)。所以,正确的表述应该是,**数组支持随机访问,根据下标随机访问的时间复杂度为 O(1)。** * 低效的 “插入” 和“删除” * 现在,如果我们需要将一个数据插入到数组中的第 k 个位置。为了把第 k 个位置腾出来,给新来的数据,我们需要将第 k~n 这部分的元素都顺序地往后挪一位。 * 插入操作的时间复杂度是如果在数组的末尾插入元素,那就不需要移动数据了,这时的时间复杂度为 O(1)。但如果在数组的开头插入元素,那所有的数据都需要依次往后移动一位,所以最坏时间复杂度是 O(n)。 因为我们在每个位置插入元素的概率是一样的,所以平均情况时间复杂度为 (1+2+...n)/n=O(n)。 数组只是被当作一个存储数据的集合。在这种情况下,如果要将某个数据插入到第 k 个位置,为了避免大规模的数据搬移,我们还有一个简单的办法就是,直接将第 k 位的数据搬移到数组元素的最后,把新的元素直接放入第 k 个位置。在特定场景下,在第 k 个位置插入一个元素的时间复杂度就会降为 O(1)。 [](https://static001.geekbang.org/resource/image/3f/dc/3f70b4ad9069ec568a2caaddc231b7dc.jpg) * 删除的理论类似,唯一区别也是在如何改成 O(1) 复杂度上,在某些特殊场景下,我们并不一定非得追求数组中数据的连续性。如果我们将多次删除操作集中在一起执行,删除的效率是不是会提高很多呢? [](https://static001.geekbang.org/resource/image/b6/e5/b69b8c5dbf6248649ddab7d3e7cfd7e5.jpg) 数组 a[10] 中存储了 8 个元素:a,b,c,d,e,f,g,h。现在,我们要依次删除 a,b,c 三个元素。 为了避免 d,e,f,g,h 这几个数据会被搬移三次,我们可以先记录下已经删除的数据。每次的删除操作并不是真正地搬移数据,只是记录数据已经被删除。当数组没有更多空间存储数据时,我们再触发执行一次真正的删除操作,这样就大大减少了删除操作导致的数据搬移。 * 容器能否完全替代数组? * ArrayList 最大的优势就是可以将很多数组操作的**细节封装起来**。比如前面提到的数组插入、删除数据时需要搬移其他数据等。另外,它还有一个优势,就是支持**动态扩容**。 * 这里需要注意一点,因为扩容操作涉及内存申请和数据搬移,是比较耗时的。所以,如果事先能确定需要存储的数据大小,**最好在创建 ArrayList 的时候事先指定数据大小。** * 是不是数组就无用武之地了呢? 1. Java ArrayList 无法存储基本类型,比如 int、long,需要封装为 Integer、Long 类,而自动装箱拆箱则有一定的性能消耗,所以如果特别关注性能,或者希望使用基本类型,就可以选用数组。 2. 如果数据大小事先已知,并且对数据的操作非常简单,用不到 ArrayList 提供的大部分方法,也可以直接使用数组。 * 为什么大多数编程语言中,数组要从 0 开始编号,而不是从 1 开始呢? * 从数组存储的内存模型上来看,“下标”最确切的定义应该是 “偏移(offset)”。前面也讲到,如果用 a 来表示数组的首地址,a[0] 就是偏移为 0 的位置,也就是首地址,a[k]就表示偏移 k 个 type_size 的位置,所以计算 a[k]的内存地址只需要用这个公式: ``` a[k]_address = base_address + k * type_size ``` 但是,如果数组从 1 开始计数,那我们计算数组元素 a[k] 的内存地址就会变为: ``` a[k]_address = base_address + (k-1)*type_size ``` 对比两个公式,我们不难发现,从 1 开始编号,每次随机访问数组元素都多了一次减法运算,对于 CPU 来说,就是多了一次减法指令。数组作为非常基础的数据结构,通过下标随机访问数组元素又是其非常基础的编程操作,效率的优化就要尽可能做到极致。所以为了减少一次减法操作,数组选择了从 0 开始编号,而不是从 1 开始。 ### 链表 * 五花八门的链表结构 * 定义 * 数组需要一块**连续的内存空间**来存储,对内存的要求比较高 * 而链表恰恰相反,它并不需要一块连续的内存空间,它通过 “指针” 将一组零散的内存块串联起来使用。 * 单链表 * 们把内存块称为链表的 **“结点”**。为了将所有的结点串起来,每个链表的结点除了存储数据之外,还需要记录链上的下一个结点的地址。如图所示,我们把这个记录下个结点地址的指针叫作**后继指针 next。** * 我们习惯性地把第一个结点叫作**头结点**,把最后一个结点叫作**尾结点**。其中,头结点用来记录链表的基地址。有了它,我们就可以遍历得到整条链表。而**尾结点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL**,表示这是链表上最后一个结点。 * 进行数组的插入、删除操作时,为了保持内存数据的连续性,需要做大量的数据搬移,所以时间复杂度是 O(n)。针对链表的插入和删除操作,我们只需要考虑相邻结点的指针改变,所以对应的时间复杂度是 O(1)。 [](https://static001.geekbang.org/resource/image/45/17/452e943788bdeea462d364389bd08a17.jpg) 有利就有弊。**链表要想随机访问第 k 个元素**,就没有数组那么高效了。因为链表中的数据并非连续存储的,所以无法像数组那样,根据首地址和下标,通过寻址公式就能直接计算出对应的内存地址,而是需要根据指针一个结点一个结点地依次遍历,直到找到相应的结点。时间复杂度为 O(n) * 双向链表 * 单向链表只有一个方向,结点只有一个**后继指针 next** 指向后面的结点。而双向链表,顾名思义,它支持两个方向,每个结点不止有一个后继指针 next 指向后面的结点,还有一个**前驱指针 prev** 指向前面的结点。 * 从结构上来看,双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点,正是这样的特点,也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。 * 从链表中删除一个数据无外乎这两种情况: * 删除结点中 “值等于某个给定值” 的结点; * 对于第一种情况,不管是单链表还是双向链表,为了查找到值等于给定值的结点,都需要从头结点开始一个一个依次遍历对比,直到找到值等于给定值的结点,然后再通过我前面讲的指针操作将其删除。 * 尽管单纯的删除操作时间复杂度是 O(1),但遍历查找的时间是主要的耗时点,对应的时间复杂度为 O(n)。根据时间复杂度分析中的加法法则,删除值等于给定值的结点对应的链表操作的总时间复杂度为 O(n)。 * 删除给定指针指向的结点。 * 对于第二种情况,我们已经找到了要删除的结点,但是删除某个结点 q 需要知道其前驱结点,而单链表并不支持直接获取前驱结点,所以,为了找到前驱结点,我们还是要从头结点开始遍历链表,直到 p->next=q,说明 p 是 q 的前驱结点。 * 但是对于双向链表来说,这种情况就比较有优势了。因为双向链表中的结点已经保存了前驱结点的指针,不需要像单链表那样遍历。所以,针对第二种情况,单链表删除操作需要 O(n) 的时间复杂度,而双向链表只需要在 O(1) 的时间复杂度内就搞定了! * 循环链表 * 而循环链表的尾结点指针是指向链表的头结点。从我画的循环链表图中,你应该可以看出来,它像一个环一样首尾相连,所以叫作 “循环” 链表。 * 链表 VS 数组性能大比拼 * 它们插入、删除、随机访问操作的时间复杂度正好相反。 * 不过,数组和链表的对比,并不能局限于时间复杂度。而且,在实际的软件开发中,不能仅仅利用复杂度分析就决定使用哪个数据结构来存储数据。数组简单易用,在实现上使用的是连续的内存空间,**可以借助 CPU 的缓存机制,预读数组中的数据,所以访问效率更高。而链表在内存中并不是连续存储,所以对 CPU 缓存不友好,没办法有效预读。** * 数组的缺点是大小固定,一经声明就要占用整块连续内存空间。如果声明的数组过大,系统可能没有足够的连续内存空间分配给它,导致 “内存不足(out of memory)”。如果声明的数组过小,则可能出现不够用的情况。这时只能再申请一个更大的内存空间,把原数组拷贝进去,非常费时。链表本身没有大小的限制,天然地支持动态扩容,我觉得这也是它与数组最大的区别。 ### 栈 * 定义 * 后进者先出,先进者后出,这就是典型的 “栈” 结构。 * 栈是一种 “操作受限” 的线性表 * 当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出、先进后出的特性,这时我们就应该首选 “栈” 这种数据结构。 * 如何实现一个 “栈”? * **用数组实现的栈**,我们叫作顺序栈 ``` public class ArrayStack<T> { private readonly int _capacity; private readonly T[] _data; private int _top = -1; // 指向栈顶元素,当为-1时表示栈为空 public ArrayStack(int capacity) { _capacity = capacity; _data = new T[capacity]; } public int Count => _top + 1; public void Push(T val) { if (Count == _capacity) throw new InvalidOperationException("Stack full."); _top++; _data[_top] = val; } public T Pop() { if (_top == -1) throw new InvalidOperationException("Stack empty."); T val = _data[_top]; _top--; return val; } } ``` 其中这里有一个细节,动态扩容,上面的版本是没有动态扩容的,细节就是容量不够了 * 增长因子倍扩容,然后搬移数据 * 用链表实现的栈,我们叫作链式栈。 ``` public class LinkedStack<T> { private StackListNode<T> _top; public int Count { get; private set; } public void Push(T val) { var newNode = new StackListNode<T>(val); newNode.Next = _top; _top = newNode; Count++; } public T Pop() { if (_top == null) throw new InvalidOperationException("Stack empty"); T val = _top.Value; _top = _top.Next; Count--; return val; } public void Clear() { while (Count > 0) { Pop(); } } } public class StackListNode<T> { public StackListNode(T nodeValue) { Value = nodeValue; } public T Value { get; set; } public StackListNode<T> Next { get; set; } } ``` * 不管是顺序栈还是链式栈,入栈、出栈只涉及栈顶个别数据的操作,所以时间复杂度都是 O(1)。 * 栈的应用 * 函数调用栈帧 * 编译器如何利用栈来实现表达式求值。 [](https://static001.geekbang.org/resource/image/bc/00/bc77c8d33375750f1700eb7778551600.jpg) * 栈在括号匹配中的应用 * 浏览器或者编辑器中的前进,后退 ### 队列 * 定义 * 先进者先出,这就是典型的 “队列” * 最基本的操作:入队 enqueue(),放一个数据到队列尾部;出队 dequeue(),从队列头部取一个元素。 * 队列跟栈一样,也是一种操作受限的线性表数据结构。 * 顺序队列和链式队列 * 用数组实现的队列叫作顺序队列。 普通拉胯版 ``` // 用数组实现的队列 public class ArrayQueue { // 数组:items,数组大小:n private String[] items; private int n = 0; // head表示队头下标,tail表示队尾下标 private int head = 0; private int tail = 0; // 申请一个大小为capacity的数组 public ArrayQueue(int capacity) { items = new String[capacity]; n = capacity; } // 入队 public boolean enqueue(String item) { // 如果tail == n 表示队列已经满了 if (tail == n) return false; items[tail] = item; ++tail; return true; } // 出队 public String dequeue() { // 如果head == tail 表示队列为空 if (head == tail) return null; // 为了让其他语言的同学看的更加明确,把--操作放到单独一行来写了 String ret = items[head]; ++head; return ret; } public void printAll() { for (int i = head; i < tail; ++i) { System.out.print(items[i] + " "); } System.out.println(); } } ``` 这里的队列满其实不是真的满,其实前面还是有空间的,假设我们还不知道循环队列的概念,那就是在满的时候吧头到尾的所有**数据搬移**到前面前面去,如下 [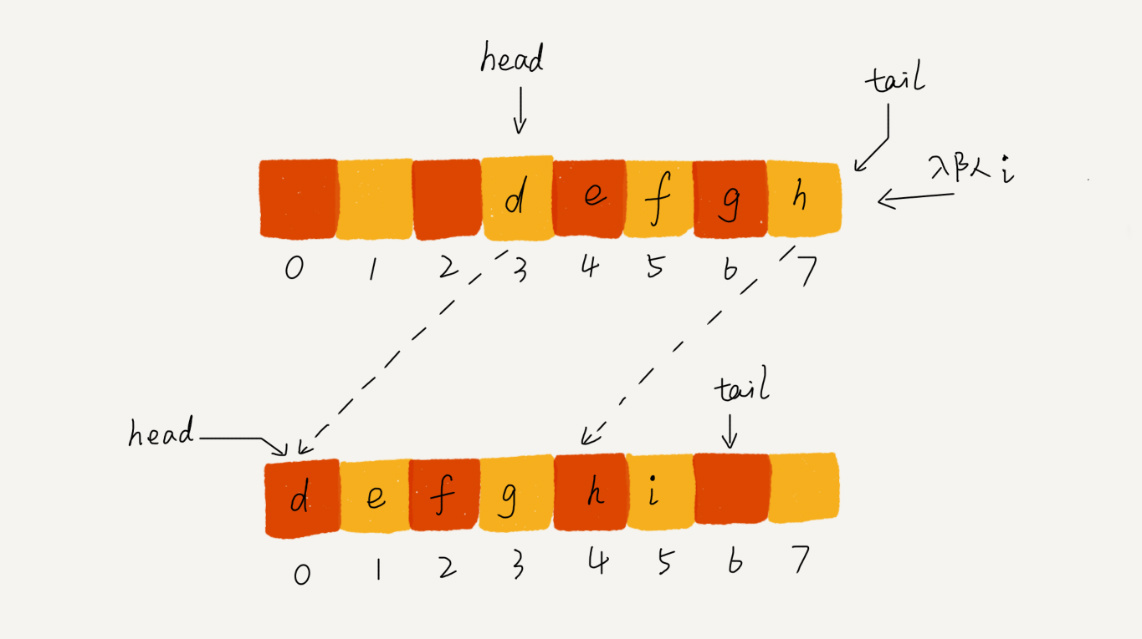](https://static001.geekbang.org/resource/image/09/c7/094ba7722eeec46ead58b40c097353c7.jpg) ``` // 入队操作,将item放入队尾 public boolean enqueue(String item) { // tail == n表示队列末尾没有空间了 if (tail == n) { // tail ==n && head==0,表示整个队列都占满了 if (head == 0) return false; // 数据搬移 for (int i = head; i < tail; ++i) { items[i-head] = items[i]; } // 搬移完之后重新更新head和tail tail -= head; head = 0; } items[tail] = item; ++tail; return true; } ``` * 用链表实现的队列叫作链式队列。 基于链表的实现,我们同样需要两个指针:head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。如图所示,入队时,tail->next= new_node, tail = tail->next;出队时,head = head->next。 ``` public class QueueBasedOnLinkedList { // 队列的队首和队尾 private Node head = null; private Node tail = null; // 入队 public void enqueue(String value) { if (tail == null) { Node newNode = new Node(value, null); head = newNode; tail = newNode; } else { tail.next = new Node(value, null); tail = tail.next; } } // 出队 public String dequeue() { if (head == null) return null; String value = head.data; head = head.next; if (head == null) { tail = null; } return value; } public void printAll() { Node p = head; while (p != null) { System.out.print(p.data + " "); p = p.next; } System.out.println(); } private static class Node { private String data; private Node next; public Node(String data, Node next) { this.data = data; this.next = next; } public String getData() { return data; } } ``` * 循环队列 * 我们刚才用数组来实现队列的时候,在 tail==n 时,会有数据搬移操作,这样入队操作性能就会受到影响。那有没有办法能够避免数据搬移呢?我们来看看循环队列的解决思路。 * 循环队列,顾名思义,它长得像一个环。原本数组是有头有尾的,是一条直线。现在我们把首尾相连,扳成了一个环。我画了一张图,你可以直观地感受一下。 [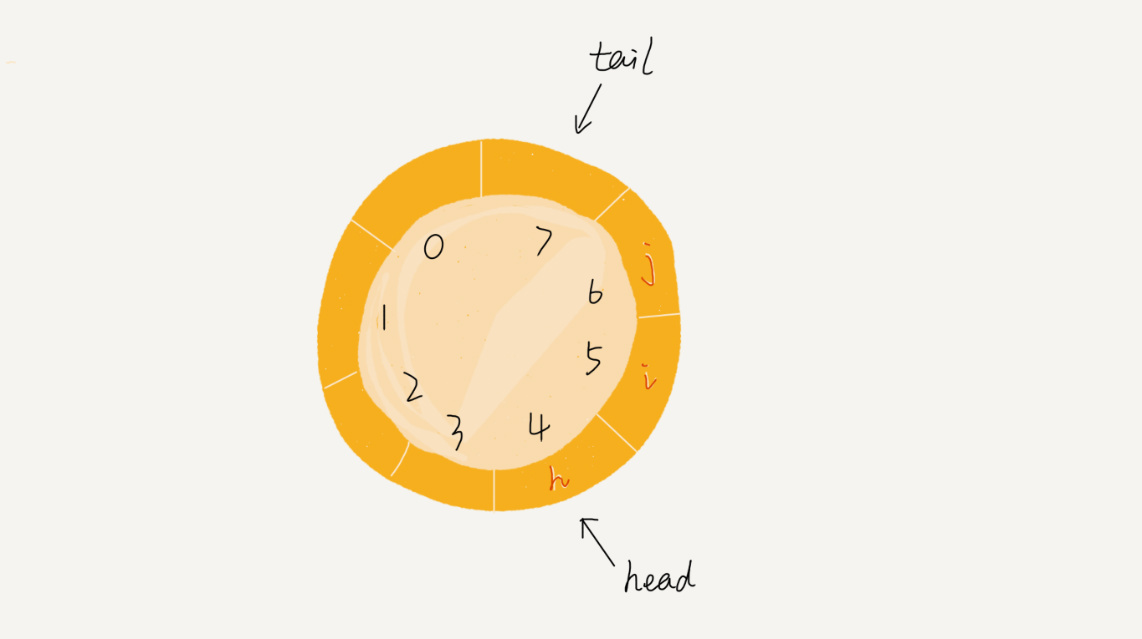](https://static001.geekbang.org/resource/image/58/90/58ba37bb4102b87d66dffe7148b0f990.jpg) 我们成功避免了数据搬移操作。看起来不难理解,但是循环队列的代码实现难度要比前面讲的非循环队列难多了。要想写出没有 bug 的循环队列的实现代码,我个人觉得,最关键的是,**确定好队空和队满的判定条件。** * 队列为空的判断条件仍然是 head == tail * 当队满时,(tail+1)%n=head。 [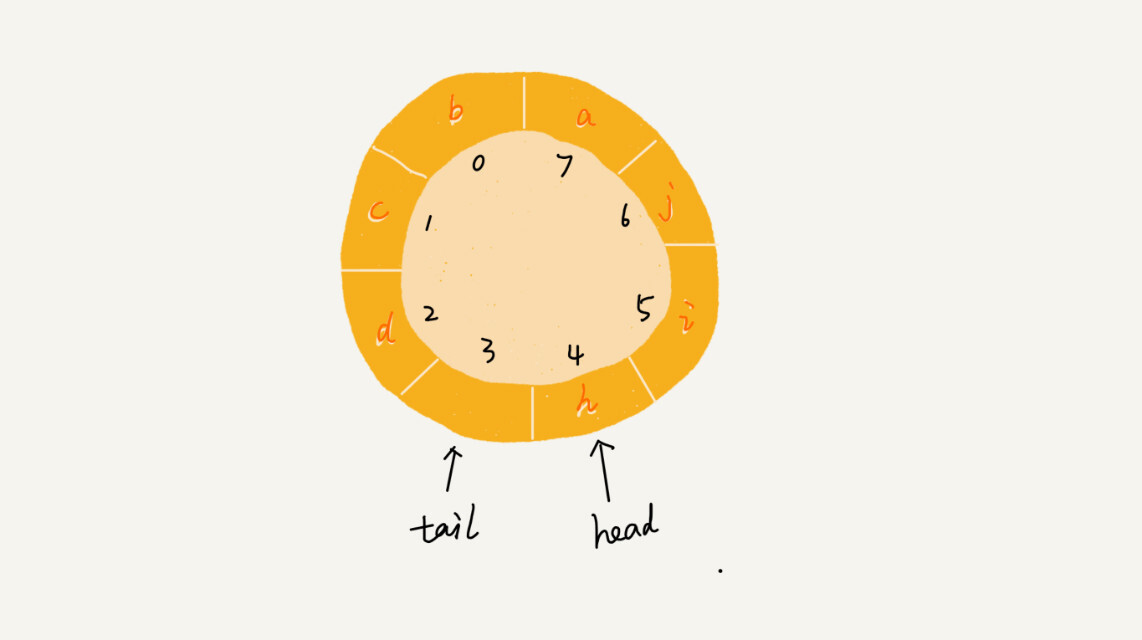](https://static001.geekbang.org/resource/image/3d/ec/3d81a44f8c42b3ceee55605f9aeedcec.jpg) ``` public class CircularQueue { // 数组:items,数组大小:n private String[] items; private int n = 0; // head表示队头下标,tail表示队尾下标 private int head = 0; private int tail = 0; // 申请一个大小为capacity的数组 public CircularQueue(int capacity) { items = new String[capacity]; n = capacity; } // 入队 public boolean enqueue(String item) { // 队列满了 if ((tail + 1) % n == head) return false; items[tail] = item; tail = (tail + 1) % n; return true; } // 出队 public String dequeue() { // 如果head == tail 表示队列为空 if (head == tail) return null; String ret = items[head]; head = (head + 1) % n; return ret; } } ``` * 应用 * 阻塞队列 阻塞队列其实就是在队列基础上增加了阻塞操作。简单来说,就是在队列为空的时候,从队头取数据会被阻塞。因为此时还没有数据可取,直到队列中有了数据才能返回;如果队列已经满了,那么插入数据的操作就会被阻塞,直到队列中有空闲位置后再插入数据,然后再返回。 * 并发队列 线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁,但是锁粒度大并发度会比较低,同一时刻仅允许一个存或者取操作。实际上,基于数组的循环队列,利用 CAS 原子操作,可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。 * **用栈实现队列** * 方法一: * 两个栈,一个负责入队一个负责出队 * 永远保持出队栈和一个空的入队栈 * 入队的时候先把出队栈依次弹出再塞回入队栈,这时候顺序就是从前到后 * 然后放入队元素 * 然后再把入队栈的数据全部弹出往出队栈丢 * 丢完后 over * 如果要出队直接从出队栈取出第一个 * 入队复杂度 O(n) 出队复杂度 O(1) * 方法二 * 这个方法和上面那方法本质上一样,但是用了一个策略,叫先等等,别急 * 因为入队和出队频率不一定一致,所以可能会是 N 次入队才有一次出队 * 这时候还是两个栈 * 入队就丢入队栈,入队时间复杂度为 O(1) * 出队的时候判断,如果出队栈是空,就把入队栈的所有数据拿出来放到出队栈里 * 这时候最上面的就是头,出就完事了 * [x] 如果出队栈不为空,就是上次没用完,就可以继续出,摊还下来,出队的时间复杂度 O(1) ### 跳表 * 定义 * 对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率就会很低,时间复杂度会很高,是 O(n)。 [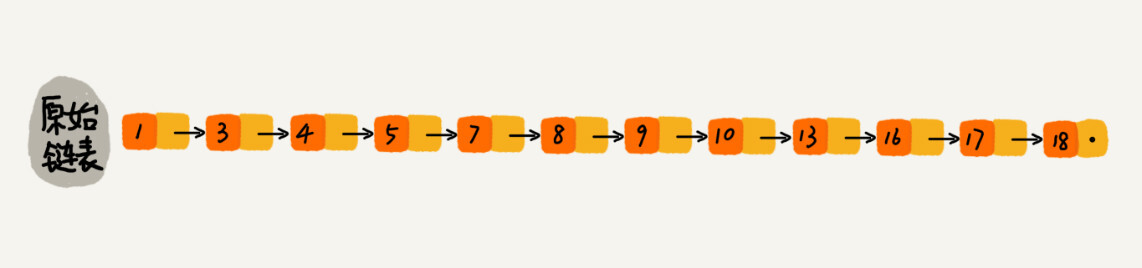](https://static001.geekbang.org/resource/image/e1/6d/e18303fcedc068e5a168de04df956f6d.jpg) * 那怎么来提高查找效率呢?如果像图中那样,对链表建立一级 “索引”,查找起来是不是就会更快一些呢?每两个结点提取一个结点到上一级,我们把抽出来的那一级叫做索引或索引层。你可以看我画的图。图中的 down 表示 down 指针,指向下一级结点。 [](https://static001.geekbang.org/resource/image/14/8e/14753c824a5ee4a976ea799727adc78e.jpg) 如果我们现在要查找某个结点,比如 16。我们可以先在索引层遍历,当遍历到索引层中值为 13 的结点时,我们发现下一个结点是 17,那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针,下降到原始链表这一层,继续遍历。这个时候,我们只需要再遍历 2 个结点,就可以找到值等于 16 的这个结点了。这样,原来如果要查找 16,需要遍历 10 个结点,现在只需要遍历 7 个结点。 * **加了一层索引之后,查找一个结点需要遍历的结点个数减少了,也就是说查找效率提高了。** * 为了让你能真切地感受索引提升查询效率。我画了一个包含 64 个结点的链表,按照前面讲的这种思路,建立了五级索引。 [](https://static001.geekbang.org/resource/image/46/a9/46d283cd82c987153b3fe0c76dfba8a9.jpg) * **前面讲的这种链表加多级索引的结构,就是跳表**。通过例子展示了跳表是如何减少查询次数的,跳表确实是可以提高查询效率的。 * 用跳表查询到底有多快? * 假设我们要查找的数据是 x,在第 k 级索引中,我们遍历到 y 结点之后,发现 x 大于 y,小于后面的结点 z,所以我们通过 y 的 down 指针,从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中,y 和 z 之间只有 3 个结点(包含 y 和 z),所以,我们在 K-1 级索引中最多只需要遍历 3 个结点,依次类推,每一级索引都最多只需要遍历 3 个结点。 [](https://static001.geekbang.org/resource/image/d0/0c/d03bef9a64a0368e6a0d23ace8bd450c.jpg) * 通过上面的分析,我们得到 m=3,所以**在跳表中查询任意数据的时间复杂度就是 O(logn)**。这个查找的时间复杂度跟二分查找是一样的。换句话说,我们其实是基于单链表实现了二分查找 * 不过,天下没有免费的午餐,这种查询效率的提升,前提是建立了很多级索引,也就是我们在第 6 节讲过的空间换时间的设计思路。 * 跳表是不是很浪费内存? * 假设原始链表大小为 n,那第一级索引大约有 n/2 个结点,第二级索引大约有 n/4 个结点,以此类推,每上升一级就减少一半,直到剩下 2 个结点。如果我们把每层索引的结点数写出来,就是一个等比数列。 * 这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以,跳表的空间复杂度是 O(n)。也就是说,如果将包含 n 个结点的单链表构造成跳表,我们需要额外再用接近 n 个结点的存储空间。那我们有没有办法降低索引占用的内存空间呢? * 我们前面都是每两个结点抽一个结点到上级索引,如果我们每三个结点或五个结点,抽一个结点到上级索引,是不是就不用那么多索引结点了呢? * 以三个为例,通过等比数列求和公式,总的索引结点大约就是 n/3+n/9+n/27+...+9+3+1=n/2。尽管空间复杂度还是 O(n),但比上面的每两个结点抽一个结点的索引构建方法,要减少了一半的索引结点存储空间。 * 实际上,在软件开发中,我们不必太在意索引占用的额外空间。在讲数据结构和算法时,我们习惯性地把要处理的数据看成整数,但是在实际的软件开发中,原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略了。 * 高效的动态插入和删除 * 如何在跳表中插入一个数据,以及它是如何做到 O(logn) 的时间复杂度的? * 在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是 O(1)。但是,这里为了保证原始链表中数据的有序性,我们需要先找到要插入的位置,这个查找操作就会比较耗时。 * 对于跳表来说,我们讲过查找某个结点的时间复杂度是 O(logn),所以这里查找某个数据应该插入的位置,方法也是类似的,时间复杂度也是 O(logn)。我画了一张图,你可以很清晰地看到插入的过程。 [](https://static001.geekbang.org/resource/image/65/6c/65379f0651bc3a7cfd13ab8694c4d26c.jpg) * 删除 * 如果这个结点在索引中也有出现,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点,然后通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点。当然,如果我们用的是双向链表,就不需要考虑这个问题了。 * **跳表索引动态更新** * **我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。** [](https://static001.geekbang.org/resource/image/c8/c5/c863074c01c26538cf0134eaf8dc67c5.jpg) * 当我们往跳表中插入数据的时候,我们可以选择同时将这个数据插入到部分索引层中。如何选择加入哪些索引层呢? * 我们通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值 K,那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。 [](https://static001.geekbang.org/resource/image/a8/a7/a861445d0b53fc842f38919365b004a7.jpg) * 随机函数的选择很有讲究,从概率上来讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。至于随机函数的选择,我就不展开讲解了。如果你感兴趣的话,可以看看 Redis 中关于有序集合的跳表实现。 * 为什么 Redis 要用跳表来实现有序集合,而不是红黑树? * Redis 中的有序集合支持的核心操作主要有下面这几个: * 插入一个数据; * 删除一个数据; * 查找一个数据; * 按照区间查找数据(比如查找值在 [100, 356] 之间的数据); * 迭代输出有序序列。 * 插入、删除、查找以及迭代输出有序序列这几个操作,红黑树也可以完成,时间复杂度跟跳表是一样的。**但是,按照区间来查找数据这个操作,红黑树的效率没有跳表高。** * 对于按照区间查找数据这个操作,跳表可以做到 O(logn) 的时间复杂度定位区间的起点,然后在原始链表中顺序往后遍历就可以了。这样做非常高效。 * 当然,Redis 之所以用跳表来实现有序集合,还有其他原因,比如,跳表更容易代码实现。虽然跳表的实现也不简单,但比起红黑树来说还是好懂、好写多了,而简单就意味着可读性好,不容易出错。还有,跳表更加灵活,它可以通过改变索引构建策略,有效平衡执行效率和内存消耗。 * 不过,跳表也不能完全替代红黑树。因为红黑树比跳表的出现要早一些,很多编程语言中的 Map 类型都是通过红黑树来实现的。我们做业务开发的时候,直接拿来用就可以了,不用费劲自己去实现一个红黑树,但是跳表并没有一个现成的实现,所以在开发中,如果你想使用跳表,必须要自己实现。 * 虽然跳表的代码实现并不简单,但是作为一种动态数据结构,比起红黑树来说,实现要简单多了。所以很多时候,我们为了代码的简单、易读,比起红黑树,我们更倾向用跳表。 ### 散列表 * 散列思想 * **散列表用的是数组支持按照下标随机访问数据的特性,所以散列表其实就是数组的一种扩展,由数组演化而来。可以说,如果没有数组,就没有散列表。** * 假设定义一个容器,要存储的是好多个对象(比如建房子给人住),hash 表的理念就是,先通过 hash 算法算出独属于每一个人的标识串(比如在现实中就是身份证号) * 然后理想状态下的容器就是一个身份证号有一个房子分配给他,这样每个人都有对应的居住地 * 但是现实很残酷,开发商经费和土地面积有限,建造的房子也就那么多(内存空间有限),所以他们就要定义一个规则让每个人能够领取自己的房间号,比如取身份证 ID 的后四位,根据后四位的值进对应的房间里住。当人数(数据量)少的时候的时候,这么做没人都有一个对应的房间,但是人一多,肯定有身份证号后四位重复的,这时候就会发生一个房间对应了多个人的情况(碰撞),那之前有人的定义就是当碰撞以后再给出一个规则比如再去身份证前 6 位去比较选到其他房间去,但是可能计算出来的房间还有人,还要继续计算(再碰撞),并且计算量也增大,所以渐渐地人们就不用这种方式了。 * 用什么方式呢,就做一个大一点的房间(链表),那如果发生了碰撞就大家都住一起,就不需要再计算了。当查询的时候,因为 hash 的计算方式,可以快速的定位出这个人的标识(对象的 hashcode)之后根据标识来去对应的房间找人,那如果这个房间住了多个人,那就按顺序一个个看是不是要找的人,虽然是线性时间的搜索,但是因为碰撞的几率小(如果碰撞的几率大就代表计算的 hash 方法不好,可以换一种 hash 的方法),搜索的效率非常快。 * hash table 的本质就是上面的概念,但是还需要注意的就是如果存储的数据大于自己的 "房间" 数时,不管哪种 hash 方法,都会发生碰撞,这时候就可以考虑扩充自己的 “房间”,降低碰撞发生概率。 * 散列函数 * 散列函数,顾名思义,它是一个函数。我们可以把它定义成 **hash(key)**,其中 key 表示元素的键值,hash(key) 的值表示经过散列函数计算得到的散列值。 * 刚刚举的学校运动会的例子,散列函数比较简单,也比较容易想到。但是,如果参赛选手的编号是随机生成的 6 位数字,又或者用的是 a 到 z 之间的字符串,该如何构造散列函数呢?我总结了三点散列函数设计的基本要求: 1. 散列函数计算得到的散列值是一个非负整数; 2. 如果 key1 = key2,那 hash(key1) == hash(key2); 3. 如果 key1 ≠ key2,那 hash(key1) ≠ hash(key2)。 * 第一点理解起来应该没有任何问题。因为数组下标是从 0 开始的,所以散列函数生成的散列值也要是非负整数。 * 第二点也很好理解。相同的 key,经过散列函数得到的散列值也应该是相同的。 * 第三点理解起来可能会有问题,我着重说一下。这个要求看起来合情合理,但是在真实的情况下,要想找到一个不同的 key 对应的散列值都不一样的散列函数,几乎是不可能的。即便像业界著名的 MD5、SHA、CRC 等哈希算法,也无法完全避免这种散列冲突。而且,因为数组的存储空间有限,也会加大散列冲突的概率。 * 散列冲突 * 开放寻址法 * 开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。那如何重新探测新的位置呢?我先讲一个比较简单的探测方法,**线性探测(Linear Probing)。** * 当我们往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,直到找到为止。 * 在散列表中查找元素的过程有点儿类似插入过程。我们通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素。如果相等,则说明就是我们要找的元素;否则就顺序往后依次查找。如果遍历到数组中的空闲位置,还没有找到,就说明要查找的元素并没有在散列表中。 * 对于使用线性探测法解决冲突的散列表,删除操作稍微有些特别。我们不能单纯地把要删除的元素设置为空。这是为什么呢? * 在查找的时候,一旦我们通过线性探测方法,找到一个空闲位置,我们就可以认定散列表中不存在这个数据。但是,如果这个空闲位置是我们后来删除的,就会导致原来的查找算法失效。本来存在的数据,会被认定为不存在。我们可以将删除的元素,特殊标记为 deleted。当线性探测查找的时候,遇到标记为 deleted 的空间,并不是停下来,而是继续往下探测。 * 线性探测法其实存在很大问题。当散列表中插入的数据越来越多时,散列冲突发生的可能性就会越来越大,空闲位置会越来越少,线性探测的时间就会越来越久。极端情况下,我们可能需要探测整个散列表,所以最坏情况下的时间复杂度为 O(n)。 * 二次探测(Quadratic probing) * 所谓二次探测,跟线性探测很像,线性探测每次探测的步长是 1,那它探测的下标序列就是 hash(key)+0,hash(key)+1,hash(key)+2…… 而二次探测探测的步长就变成了原来的 “二次方”,也就是说,它探测的下标序列就是 hash(key)+0,hash(key)+12,hash(key)+22…… * 双重散列(Double hashing) * 所谓双重散列,意思就是不仅要使用一个散列函数。我们使用一组散列函数 hash1(key),hash2(key),hash3(key)…… 我们先用第一个散列函数,如果计算得到的存储位置已经被占用,再用第二个散列函数,依次类推,直到找到空闲的存储位置。 * 不管采用哪种探测方法,当散列表中空闲位置不多的时候,散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率,一般情况下,我们会尽可能保证散列表中有一定比例的空闲槽位。我们用**装载因子(load factor)**来表示空位的多少 * 装载因子的计算公式是:`散列表的装载因子=填入表中的元素个数/散列表的长度` * 装载因子越大,说明空闲位置越少,冲突越多,散列表的性能会下降。 * 链表法 * 链表法是一种更加常用的散列冲突解决办法,相比开放寻址法,它要简单很多。我们来看这个图,在散列表中,每个 “桶(bucket)” 或者 “槽(slot)” 会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。 [](https://static001.geekbang.org/resource/image/a4/7f/a4b77d593e4cb76acb2b0689294ec17f.jpg) * 当插入的时候,我们只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是 O(1)。当查找、删除一个元素时,我们同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。 * 查找或删除操作的时间复杂度跟链表的长度 k 成正比,也就是 O(k)。对于散列比较均匀的散列函数来说,理论上讲,k=n/m,其中 n 表示散列中数据的个数,m 表示散列表中 “槽” 的个数。 * 如何打造一个工业级水平的散列表? * 如何设计散列函数? * 散列函数的设计不能太复杂 * 散列函数生成的值要尽可能随机并且均匀分布 * 装载因子过大了怎么办? * 对于动态散列表来说,数据集合是频繁变动的,我们事先无法预估将要加入的数据个数,所以我们也无法事先申请一个足够大的散列表。随着数据慢慢加入,装载因子就会慢慢变大。当装载因子大到一定程度之后,散列冲突就会变得不可接受。 * **动态扩容**,针对数组的扩容,数据搬移操作比较简单。但是,针对散列表的扩容,数据搬移操作要复杂很多。因为散列表的大小变了,数据的存储位置也变了,所以我们需要通过散列函数重新计算每个数据的存储位置。 [](https://static001.geekbang.org/resource/image/67/43/67d12e07a7d673a9c1d14354ad029443.jpg) * 插入一个数据,最好情况下,不需要扩容,最好时间复杂度是 O(1)。最坏情况下,散列表装载因子过高,启动扩容,我们需要重新申请内存空间,重新计算哈希位置,并且搬移数据,所以时间复杂度是 O(n)。用摊还分析法,**均摊情况下,时间复杂度接近最好情况,就是 O(1)。** * 实际上,对于动态散列表,随着数据的删除,散列表中的数据会越来越少,空闲空间会越来越多。如果我们对空间消耗非常敏感,**我们可以在装载因子小于某个值之后,启动动态缩容。**当然,如果我们更加在意执行效率,能够容忍多消耗一点内存空间,那就可以不用费劲来缩容了。 * 装载因子阈值需要选择得当。如果太大,会导致冲突过多;如果太小,会导致内存浪费严重。 * 装载因子阈值的设置要权衡时间、空间复杂度。如果内存空间不紧张,对执行效率要求很高,可以降低负载因子的阈值;相反,如果内存空间紧张,对执行效率要求又不高,可以增加负载因子的值,甚至可以大于 1。 * 如何避免低效的扩容? * 我举一个极端的例子,如果散列表当前大小为 1GB,要想扩容为原来的两倍大小,那就需要对 1GB 的数据重新计算哈希值,并且从原来的散列表搬移到新的散列表,听起来就很耗时,是不是? * 如果我们的业务代码直接服务于用户,尽管大部分情况下,插入一个数据的操作都很快,但是,极个别非常慢的插入操作,也会让用户崩溃。这个时候,“一次性” 扩容的机制就不合适了。 * **为了解决一次性扩容耗时过多的情况,我们可以将扩容操作穿插在插入操作的过程中,分批完成。当装载因子触达阈值之后,我们只申请新空间,但并不将老的数据搬移到新散列表中。** * 有新数据要插入时,我们将新数据插入新散列表中,并且从老的散列表中拿出一个数据放入到新散列表。每次插入一个数据到散列表,我们都重复上面的过程。经过多次插入操作之后,老的散列表中的数据就一点一点全部搬移到新散列表中了。这样没有了集中的一次性数据搬移,插入操作就都变得很快了。 [](https://static001.geekbang.org/resource/image/6d/cb/6d6736f986ec4b75dabc5472965fb9cb.jpg) * 这期间的查询操作怎么来做呢?对于查询操作,为了兼容了新、老散列表中的数据,我们先从新散列表中查找,如果没有找到,再去老的散列表中查找。通过这样均摊的方法,将一次性扩容的代价,均摊到多次插入操作中,就避免了一次性扩容耗时过多的情况。 * 这种实现方式,任何情况下,插入一个数据的时间复杂度都是 O(1)。 * 如何选择冲突解决方法? * 开放寻址法 * 开放寻址法不像链表法,需要拉很多链表。散列表中的数据都存储在数组中,可以有效地利用 CPU 缓存加快查询速度。而且,这种方法实现的散列表,序列化起来比较简单。链表法包含指针,序列化起来就没那么容易。 * 用开放寻址法解决冲突的散列表,删除数据的时候比较麻烦,需要特殊标记已经删除掉的数据。而且,在开放寻址法中,所有的数据都存储在一个数组中,比起链表法来说,冲突的代价更高。所以,使用开放寻址法解决冲突的散列表,装载因子的上限不能太大。**这也导致这种方法比链表法更浪费内存空间。** * **当数据量比较小、装载因子小的时候,适合采用开放寻址法。这也是 Java 中的 ThreadLocalMap 使用开放寻址法解决散列冲突的原因。** * 链表法 * 链表法对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建,并不需要像开放寻址法那样事先申请好。实际上,这一点也是我们前面讲过的链表优于数组的地方。 * 链表法比起开放寻址法,对大装载因子的容忍度更高。开放寻址法只能适用装载因子小于 1 的情况。 * 链表因为要存储指针,所以对于比较小的对象的存储,是比较消耗内存的,还有可能会让内存的消耗翻倍。而且,因为链表中的结点是零散分布在内存中的,不是连续的,所以对 CPU 缓存是不友好的,这方面对于执行效率也有一定的影响。 * 当然,如果我们存储的是大对象,也就是说要存储的对象的大小远远大于一个指针的大小(4 个字节或者 8 个字节),那链表中指针的内存消耗在大对象面前就可以忽略了。 * 我们对链表法稍加改造,可以实现一个更加高效的散列表。那就是,**我们将链表法中的链表改造为其他高效的动态数据结构,比如跳表、红黑树。**这样,即便出现散列冲突,极端情况下,所有的数据都散列到同一个桶内,那最终退化成的散列表的查找时间也只不过是 O(logn)。这样也就有效避免了前面讲到的散列碰撞攻击。 [](https://static001.geekbang.org/resource/image/10/29/103b84d7173277c5565607b413c40129.jpg) * 基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表,而且,比起开放寻址法,它更加灵活,支持更多的优化策略,比如用红黑树代替链表。 * 应用举例 * Java 中的 HashMap * 初始大小 * HashMap 默认的初始大小是 16,当然这个默认值是可以设置的,如果事先知道大概的数据量有多大,可以通过修改默认初始大小,减少动态扩容的次数,这样会大大提高 HashMap 的性能。 * 装载因子和动态扩容 * 最大装载因子默认是 0.75,当 HashMap 中元素个数超过 0.75*capacity(capacity 表示散列表的容量)的时候,就会启动扩容,每次扩容都会扩容为原来的两倍大小。 * 散列冲突解决方法 * HashMap 底层采用链表法来解决冲突。即使负载因子和散列函数设计得再合理,也免不了会出现拉链过长的情况,一旦出现拉链过长,则会严重影响 HashMap 的性能。 * 在 JDK1.8 版本中,为了对 HashMap 做进一步优化,我们引入了红黑树。而当链表长度太长(默认超过 8)时,链表就转换为红黑树。我们可以利用红黑树快速增删改查的特点,提高 HashMap 的性能。当红黑树结点个数少于 8 个的时候,又会将红黑树转化为链表。因为在数据量较小的情况下,红黑树要维护平衡,比起链表来,性能上的优势并不明显。 * 散列函数 * 散列函数的设计并不复杂,追求的是简单高效、分布均匀。 ``` int hash(Object key) { int h = key.hashCode(); return (h ^ (h >>> 16)) & (capicity -1); //capicity表示散列表的大小 } ``` * 什么是哈希算法 * 哈希算法的定义和原理非常简单,基本上一句话就可以概括了。将任意长度的二进制值串映射为固定长度的二进制值串,**这个映射的规则就是哈希算法**,而通过原始数据映射之后得到的二进制值串就是哈希值。但是,要想设计一个优秀的哈希算法并不容易,根据我的经验,我总结了需要满足的几点要求: * 从哈希值不能反向推导出原始数据(所以哈希算法也叫单向哈希算法); * 对输入数据非常敏感,哪怕原始数据只修改了一个 Bit,最后得到的哈希值也大不相同; * 散列冲突的概率要很小,对于不同的原始数据,哈希值相同的概率非常小; * 哈希算法的执行效率要尽量高效,针对较长的文本,也能快速地计算出哈希值。 * 哈希算法的应用非常非常多,最常见的七个分别是安全加密、唯一标识、数据校验、散列函数、负载均衡、数据分片、分布式存储。 * **散列表两个核心问题是散列函数设计和散列冲突解决。** 参考资料 ==== * [数据结构与算法之美](https://time.geekbang.org/column/article/42520) * [数据结构和算法必知必会的 50 个代码实现](https://github.com/wangzheng0822/algo) __EOF__ 数据结构与算法知识树整理——算法篇——排序 数据结构与算法知识树整理——数据结构篇——非线性结构