树状数组从入门到下车 agile Posted on Jul 14 2023 数据结构与算法 yukiyama --- title: 树状数组从入门到下车 tags: - 树状数组 - 区间问题 - 算法与数据结构 categories: 算法与数据结构 description: >- 树状数组是一种能够高效求解「区间问题」的数据结构。「区间问题」指的是对于大小为 n 的输入数组 nums ,通过其上执行「区间求和」、「区间修改」等操作 (通过不同类型的树状数组) 来处理的问题,解决区间问题的过程中通常还伴随着针对单个元素的「单点查询」、「单点修改」这两种单点操作。 cover: >- https://raw.githubusercontent.com/iyukiyama/pics/master/hexo-iyukiyama/site_img/posts/algorithms/fenwick-bg.png katex: true abbrlink: binary-indexed-tree keywords: top_img: comments: --- # 树状数组从入门到下车 **感谢官方推荐** 🎉😄。 > - 可在作者的 [github仓库](https://github.com/iyukiyama/leetcode-posts) 中获取本文和其他文章的 markdown 源文件及相关代码。 > > - 欢迎评论或仓库 PR 指出文章错漏或与我讨论相关问题,我将长期维护所有文章。 > - 所有文章均用 Typora 完成写作,可使用 Typora 打开文章 md 文件,以获得最佳阅读体验。 ⚠️⚠️⚠️ **全文一万四千字,外科手术式讲解三种树状数组。抽象的,我们让它具体,难解的,我们条分缕析。** ❗️ **【NEW】** ❗️ - 9-15: [红黑树从入门到看开](https://leetcode.cn/circle/discuss/SwgIJV/) 这是小白 yuki 推出的「树ADT」系列文章的第 10 篇 (10/13) 。 *** > $keywords$ : > > 树状数组 (BIT) / 区间划分 / 前缀和 / $lowbit$ / 单点修改 (Point Update, PU) / 单点查询 (Point Query, PQ) / 区间修改 (Range Update, RU) / 区间查询 (Range Query, RQ) / 单改区查 (PURQ BIT) / 区改单查 (RUPQ BIT) / 区改区查 (RURQ BIT) / 差分数组 / 离散化 (松离散 & 紧离散) / 指定区间在给定取值范围内的元素数 **树状数组** 是一种能够高效求解「区间问题」的数据结构。「区间问题」指的是对于大小为 $n$ 的输入数组 $nums$ ,通过其上执行「区间求和」、「区间修改」等操作 (通过不同类型的树状数组) 来处理的问题,解决区间问题的过程中通常还伴随着针对单个元素的「单点查询」、「单点修改」这两种单点操作。若直接根据下标操作 $nums$ ,则单点操作时间复杂度为 $O(1)$ ,而区间操作为 $O(n)$ ;若采用「前缀和」,则区间操作为 $O(1)$ ,而单点操作为 $O(n)$ 。 本文将介绍的树状数组,利用 $nums$ 的 **下标二进制表示及其位运算** ,十分巧妙地将输入区间划分为 $n$ 个子区间,使得这些区间构成一棵或多棵多叉树,这些树通过一个数组表达,即所谓「树状数组」。借助树状数组的逻辑树形结构,能够 **同时实现 $O(logn)$ 时间复杂度的单点操作与区间操作** 。 上述文字是对树状数组的高度概括,初学时必然难解其意,但只要读者学完本文,一定会对上述描述有深刻的理解。本文主要内容及编排顺序如下。 1. **基本树状数组 (单点修改区间查询树状数组)** : 以 $O(logn)$ 时间复杂度解决长度为 $n$ 的序列的 **单点修改** 及 **区间查询** 问题。 2. **区间划分:** 从区间查询问题出发,思考如何利用类似倍增思想的做法来划分子区间,从而提高区间查询的效率。 3. **lowbit:** 由「划分连续子区间」的需求出发,尝试从元素下标二进制表示入手,找到通过 $lowbit$ 求子区间 (左右界) 的方式,所有子区间构成一棵或多棵逻辑上的多叉的 **「二元索引树」** 。 4. **时间复杂度分析:** 单点修改及区间查询的时间复杂度都与 $(n)_2$ 的位数相关,简单分析后可知它们都是时间为 $O(logn)$ 的操作。 5. **区间修改单点查询树状数组:** 在「单点修改区间查询树状数组」的基础上,引入 **差分数组** 实现区间修改单点查询树状数组。 6. **区间修改区间查询树状数组:** 在「区间修改单点查询树状数组」的基础上,根据 **算式推导** ,引入 **辅助树状数组** 实现区间修改区间查询树状数组。 7. **离散化** : 当区间问题只关心元素之间的大小关系而不关心元素值时,将输入序列离散化,能够提高求解效率或帮助解决一些特定问题。离散化实现包括 **松离散** 和 **紧离散** 。 8. **指定区间内指定取值范围的元素数**:「求指定区间 $[l,r]$ 内大小在指定取值范围 $[lower, upper]$ 内的元素数」是一类特定的可用树状数组巧妙解决的问题。 本文原题 「树状数组 (树ADT连载 10/13)」,十分干瘪,不太符合作者的气质,遂改为现标题。**「下车」表示作者的一种希望**,此刻我们开始发车学习树状数组,看完本文,希望读者朋友们能轻松掌握,安全下车。 *** yuki的其他文章如下,欢迎阅读指正! > 如下所有文章同时也在我的 github [仓库](https://github.com/iyukiyama/leetcode-posts) 中维护。 | 文章 | [发布时间] 字数/览/藏/赞 (~2022-10-20) | | ------------------------------------------------------------ | ---------------------------------------- | | [十大排序从入门到入赘](https://leetcode.cn/circle/discuss/eBo9UB/) 🔥🔥🔥 | [20220516] 2.5万字/64.8k览/3.7k藏/937赞 | | [二分查找从入门到入睡](https://leetcode.cn/circle/discuss/ooxfo8/) 🔥🔥🔥 | [20220509] 2.3万字/38.4k览/2.1k藏/503赞 | | [并查集从入门到出门](https://leetcode.cn/circle/discuss/qmjuMW/) 🔥🔥 | [20220514] 1.2万字/17.9k览/1.0k藏/321赞 | | [图论算法从入门到放下](https://leetcode.cn/circle/discuss/FyPTTM/) 🔥🔥 | [20220617] 5.6万字/19.9k览/1.3k藏/365赞 | | 树ADT系列 (预计13篇) | 系列文章,连载中 | | 3. [二叉查找树](https://leetcode.cn/circle/discuss/wPzlSb/) | [20220801] 5千字 | | 4. [AVL树](https://leetcode.cn/circle/discuss/zbwD3p/) | [20220817] 5千字 | | 5. [splay树](https://leetcode.cn/circle/discuss/BCK17f/) | [20220817] 5千字 | | 6. [红黑树从入门到看开](https://leetcode.cn/circle/discuss/SwgIJV/) 🔥🤯🤯🤯 | [20220915] 3万字/5.3k览/269藏/72赞 | | 10. [树状数组从入门到下车](https://leetcode.cn/circle/discuss/qGREiN/) 🔥🤯 | [20220722] 1.4万字/5.8k览/196藏/72赞 | | 11. [线段树从入门到急停](https://leetcode.cn/circle/discuss/H4aMOn/) 🔥🤯 | [20220726] 2.5万字/8.7k览/481藏/138赞 | | [图论相关证明系列](https://leetcode.cn/circle/discuss/GV0JrV/) | 系列文章 | | 1. [Dijkstra正确性证明](https://leetcode.cn/circle/discuss/jJQn7V/) 🤯 | [20220531] | | 2. [Prim正确性证明](https://leetcode.cn/circle/discuss/VVEc8f/) 🤯 | [20220919] | | 3. [Bellman-Ford及SPFA正确性证明](https://leetcode.cn/circle/discuss/xeEwYl/) | [20220602] | | 4. [Floyd正确性证明](https://leetcode.cn/circle/discuss/Nbzix4/) | [20220602] | | 5. [最大流最小割定理证明](https://leetcode.cn/circle/discuss/tMIy36/) 🤯🤯 | [20220719] | | 6. [Edmonds-Karp复杂度证明](https://leetcode.cn/circle/discuss/tN3sZc/) 🤯🤯 | [20220515] | | 7. [Dinic复杂度证明](https://leetcode.cn/circle/discuss/T9Xa1R/) 🤯🤯 | [20220531] | *** [2022-10-16] - 再次重写「指定区间内指定取值范围的元素数」一节 (重写三回了。。。😅)。 [2022-10-15] - 将原先 $tree$ 的有效下标为 $[1,n]$ 改为更容易理解的 $[0,n-1]$ ,相应地,修改了三种 BIT 类的实现代码以适应这一调整。一并修改了大部分配图。 - 几乎重写了「指定区间内指定取值范围的元素数」一节。 [2022-10-14] - 修正了两幅配图。 - 大幅修改了三种 BIT 类的实现代码,修改后更易于理解。 *** [TOC] *** ## 树状数组 [树状数组](https://en.wikipedia.org/wiki/Fenwick_tree) (二元索引树 / 二元下标树 / Binary Indexed Tree, BIT / Fenwick Tree): 树状数组虽名为数组,但从其英文名 (Binary Indexed Tree) 可看出它本质上是一种被表达为树的数据结构。对于大小为 $n$ 的序列 $nums$ ,最基本的树状数组以 $O(logn)$ 时间复杂度同时支持如下两种操作。 - 更新 $nums$ 中单个元素的值,即 **单点修改** 。 - 求 $nums$ 任意区间的元素值之和,即 **区间查询** 。 对于这两种操作,最简单的做法是直接根据下标操作 $nums$ ,单点修改的时间复杂度为 $O(1)$ ,区间查询为 $O(n)$ 。此外,我们也可以利用「前缀和」来完成。首先计算出 $nums$ 的前缀和数组 $preSum$ ,那么求 $[l , r]$ 区间和,即是求 $preSum[r] - preSum[l-1]$ ,时间复杂度为 $O(1)$ 。但单点修改 $nums[i]$ 时,需要更新 $preSum[i]$ 及之后的前缀和数组元素 (否则之后求区间和会出错),这使得单点修改时间复杂度为 $O(n)$ 。 无论是使用普通数组还是利用前缀和数组,对于上述两种操作,均有一种的时间复杂度为 $O(n)$ 。而树状数组通过维护一个与 $nums$ 等大的,在逻辑上为树状结构 (一棵或多棵多叉树) 的数组 $tree[]$ ,使得两种操作的时间复杂度均为 $O(logn)$ 。 | 序列操作 | 数组 | 前缀和 | 树状数组 | | -------- | ------ | ------ | --------- | | 单点修改 | $O(1)$ | $O(n)$ | $O(logn)$ | | 区间查询 | $O(n)$ | $O(1)$ | $O(logn)$ | **树状数组是一种极具巧思,代码实现极轻巧却不失高效的数据结构** 。我们马上会看到树状数组如何借助 **二进制形式的 $nums$ 的下标值** ,将 $nums$ 划分为多个子区间,这些子区间构成逻辑树形结构,利用树的特点使得两种基本操作都复杂度都是 $O(logn)$ 。 为方便后续行文,我们提前介绍如下操作,并约定称呼及简称。 | 操作 | 定义 | | --------------------------- | ---------------------------------------------------- | | 单点修改 (Point Update, PU) | 修改 $nums$ 的单个元素 | | 单点查询 (Point Query, PQ) | 查询 $nums$ 的单个元素 | | 区间修改 (Range Update, RU) | 修改 $nums$ 的某个区间<br />※ 区间元素都加上同一个数 | | 区间查询 (Range Query, RQ) | 求 $nums$ 的某个区间的区间和 | > 根据 wiki,树状数组最早由 Boris Ryabko (前苏联) 于1989年 [提出](http://boris.ryabko.net/dan1989.pdf) ,并在1992 年发表了一个 [改进版本](http://boris.ryabko.net/ryabko1992.pdf) 。 Peter Fenwick 在其1994年的 [文章](https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.14.8917) 中描述了该数据结构,随后此数据结构便以 Fenwick tree 之名广为人知。 > > This structure was proposed by Boris Ryabko in 1989[[1\]](https://en.wikipedia.org/wiki/Fenwick_tree#cite_note-1) with a further modification published in 1992.[[2\]](https://en.wikipedia.org/wiki/Fenwick_tree#cite_note-2) It has subsequently become known under the name Fenwick tree after [Peter Fenwick](https://en.wikipedia.org/w/index.php?title=Peter_Fenwick_(computer_scientist)&action=edit&redlink=1), who described this structure in his 1994 article.[[3\]](https://en.wikipedia.org/wiki/Fenwick_tree#cite_note-3) > > > > 作者的「树状数组」知识,最初学自 OI wiki [树状数组](https://oi-wiki.org/ds/fenwick/)。 <br /> ### PURQ BIT (单改区查) 最基本的树状数组支持「单点修改 (PU)」和「区间查询 (RQ)」,即 PURQ BIT。 <br /> #### 区间划分 我们已经知道,使用普通数组或利用前缀和数组实现 PU / RQ 操作时,各自均有一种操作需要遍历 **一段连续的区间** 。在 $nums$ 上的「连续」操作的时间复杂度为 $O(n)$ 。为了提高操作效率,我们必须 **减少操作的次数** 。首先考虑求长度为 $k$ 的区间的区间和操作,我们会想,如果不是连续地相加 $k$ 次,而是通过某种预先处理的手段,将大小为 $k$ 的区间 **划分为多个子区间** ,子区间个数显著地少于 $k$ ,每一个子区间的区间和都被高效地实时维护,那么求区间和时,就只需要执行远少于 $k$ 次的加运算 (子区间的区间和相加) 。 例如下图,当我们求 $nums$ 区间 $[3, 8]$ 的区间和时,如果我们能通过某种方式,找到子区间 $[3,4]$ 、 子区间 $[5,7]$ 、子区间 $[8,8]$ ,且这些子区间的区间和总是能够被实时维护,那么只需将这三个子区间的和相加即可,原先需要将 6 个数相加,现在只需要将 3 个数相加,这样就减少了操作的次数。  **那么树状数组是这一想法的实现吗?答案是:不完全是。** 树状数组确实将 $nums$ 划分成了多个区间,但并不是对任意区间 $[l,r]$ 划分连续子区间,而是通过 **「前缀区间和」作差** 的方式来得到指定区间的「区间和」,前缀区间才是通过若干个连续子区间组成的。 我们提前指出,树状数组这一数据结构,对输入数组 $nums$ 划分为多个子区间,使得对任意的 $[0,k]$ 前缀区间,都可以 **由划分结果中的若干个连续的子区间构成** ,这些子区间的区间和相加即可得到「前缀区间和」。对于任意区间 $[l,r]$ ,将右界前缀区间 $[0, r]$ 的区间和减去左界前一位的前缀区间 $[0,l-1]$ 的区间和,即为 $[l,r]$ 区间和。 区间划分的思考也许会让你想到利用「倍增思想」的快速幂算法 [leetcode #50-pow(x, n)](https://leetcode-cn.com/problems/powx-n/) ,该算法不是通过「连续」地将 $x$ 相乘 $n$ 次,而总是借助已经算出的结果来快速得到新的更大范围的中间结果,这个中间结果又能用于之后求更大范围的结果的计算中。实际上除了倍增思想,动态规划、记忆化搜索都体现了这种 **「利用已求出的结果完成下一步计算」** 的思想。总之我们需要一种类似倍增方法的能够跳跃式划分区间 (下标) 的方法。 现在,我们重新将 **树状数组解决区间和问题** 的 **灵感来源** 描述如下: - $nums$ 上任意 $[l, r]$ 的区间和,将通过 $[0,r]$ 和 $[0, l-1]$ 的「前缀区间和」作差得到。 - 前缀区间由若干个相邻的子区间构成,这些子区间的区间和相加得到前缀区间的区间和。 - 也许能够通过某种类似倍增方式划分 $nums$ 的下标 (从倍增法得到的灵感)。 很抽象,尤其是最后一句,现在无法得知如何处理下标来划分输入区间,不过没关系,我们马上对大小为 8 (下标范围为 $[0,7]$)的 $nums$ 实践上述描述。 首先明确为了实现「更快地求区间和」的需求: 1. 将指定长度的 $nums$ 划分为若干区间。对 $nums$ 下标的划分动作应当是一种 **可循环的操作** 。 2. $nums$ 上的任意区间 $[l, r]$ 的区间和可由 $[0,r]$ 区间和与 $[0,l-1]$ 区间和作差得到,这是「前缀和」思想。这要求 $[0, l-1], [0,r]$ 均由 $nums$ 划分结果中的 **若干相邻区间** 所构成。从这里可以看出, 对 $nums$ 的划分,不只是对 $[0,n-1]$ 的划分,而是对 $[0,k](k∈[0,n-1])$ 的划分。划分结果必须满足能由若干连续区间构成任意的 $[0,k](k∈[0,n-1])$ 区间 (这句话是理解树状数组的关键,请读者在阅读后文时反复体会)。 3. 子区间的区间和被 **实时维护** 。需要用一个 $tree[]$ 数组保存所有子区间和 (我们马上会知道为什么命名为 $tree$)。 4. 求给定区间的区间和,即求两次前缀区间和再作差。求前缀区间和需要通过 **某种规则** 一边寻找其子区间 $i$ (连续的) ,一边将 $tree[i]$ (子区间 $i$ 的区间和) 累计到结果中。 5. 更新 $nums[i]$ 时,通过 **某种规则** 更新包含该值的所有子区间的区间和。 「灵感来源」描述中提到了「类似倍增方式」,我们不难想到可以从下标的二进制表示着手。以划分区间 $[0,14]$ 为例,先写出 14 的二进制表示 $14=(1110)_2$ 。我们要求划分动作是可循环的操作,且对于任意长度的 $nums$,都能通过同样的方式完成划分。划分区间就是要确定区间的左右界。很直接地,区间 $[0,14]$ 的 **最右子区间的右界** 为 14 , **最左子区间的左界** 是 0 。我们将最右子区间作为当前区间,从当前子区间右界下标 14 开始考虑。 一个容易想到的方法如下: > 【区间划分方法】:从最右子区间右界 $k$ 开始,将 $k$ 的最低位 1 换成 0 ,新的 $k$ 作为当前区间的左界下标,减 1 即为其 **左邻子区间的右界下标** 。重复该操作直到当前区间右界下标为 0 (二进制数所有位都没有 1) 。 于是区间 $[0,14]$ 被划分为这三个区间 $[(0000)_2,(1000)_2)$ , $[(1000)_2,(1100)_2)$ , $[(1100)_2,(1110)_2]$ ,即 $[0,7]$ , $[8,11]$ , $[12,14]$。我们一方面保证了划分动作是循环的,同时也保证了划分后的子区间是连续的。但还存在一个小问题,当划分到最后一个子区间 $[(0000)_2,(1000)_2)$ 时,左界为 0 ,应当要退出划分区间的循环,但此时需要处理最后一个区间 ($[0,7]$),不能直接退出,于是我们利用下一次左界「也是」0 来作为退出划分区间循环的判断条件。但要记录连续两次左界,这似乎有点麻烦,实际上我们只需做一个小调整,即可更优雅地结束划分。 仍以 $[0,14]$ 为例,我们不直接使用 14 而是使用 $14+1=15$ 的二进制表示 $15=(1111)_2$ 作为划分起始点 $i$ (这里的 $i$ 不是下标,而是右界下标 $k$ 加 1)。划分方法与之前相同。按照该方式,区间 $[0,14]$ 从右到左被依次被划分为。 - $[(1110)_2,(1111)_2)$ (即 $[14,14]$) - $[(1100)_2,(1110)_2)$ (即 $[12,13]$) - $[(1000)_2,(1100)_2)$ (即 $[8,11]$) - $[(0000)_2,(1000)_2)$ (即 $[0,7]$) 利用该方法,我们一方面保证了划分动作是循环的,同时也保证了划分后的子区间是连续的,还保证了循环能够退出,即一定会完成划分。实际上经过验证后,我们发现,这样的区间划分方式完全符合前述 5 点要求,对照说明如下。 1. 规则是固定的,因此操作是可循环的,通过这种方式,我们一定能够将 $nums$ 的任意 $[0, k]$ 区间划分为一些子区间。 也容易看出,$[0,k]$ 无论怎么划分, **一定有且只有一个以 $k$ 为右界的子区间** 。$k$ 的取值有 $n$ 种 ($0 \sim n-1$),因此 **长度为 $n$ 的 $nums$ 划分出 $n$ 个子区间** ,这些子区间的右界是 $\{0,1,2,...,n-1\}$ ,左界通过 $(k+1)-lowbit(k+1)$ 求出,即 $\{1-lowbit(1),2-lowbit(2),3-lowbit(3),...,n-lowbit(n)\}$ ($lowbit(i)$ 就是最低位 1 所代表的数字,后续介绍其实现)。 2. 根据 1,对于任意的 $[l,r]$ ,一定有对应的由一个或多个连续区间构成的「前缀区间」 $[0,l-1]$ 和 $[0,r]$ ,将二者的区间和作差即可得到 $[l,r]$ 的区间和。 3. 单点修改会导致所有包含被修改的元素值的区间的区间和发生变动,需要对这些区间的区间和做同样的更新操作。现在我们还不知道要怎么找 「**包含给定元素的所有区间」** ,留到后续说明。 4. 「将当前子区间右界下标最低位的 1 换成 0」的划分方式即为该规则 (即 $lowbit()$ 方法)。 5. 同 3,后续说明。 至此,我们终于可以描述「树状数组」 $tree[]$ 。 - 划分得到 $n$ 个子区间,每一个子区间的右界元素都唯一地存在于该区间中,因此当我们要表示区间的区间和时,可用该区间右界作为 $tree[]$ 的下标,例如 $tree[5]$ 指的是右界为 5 的区间的区间和 (只有该区间包含了 $nums[5]$) 。 - 由上述,$tree$ 的大小与 $nums$ 相同,为 $n$ 。 - 以 $k$ 为右界的区间的左界为 $(k+1)-lowbit(k+1)$ 。$lowbit$ 方法即划分区间的位运算实现。 还是很抽象?再坚持一下,介绍 $lowbit$ 方法后上图,外科手术式解析。 <br /> ##### lowbit 前面我们说过「将当前子区间右界 $k$ 加 1后的 $k+1$ 的二进制表示中最低位的 1 换成 0 后作为该子区间左界」。在代码中我们通过巧妙的位运算来实现这一更新。 下图以两个例子 (110101, 101000) 展示这一运算过程,也即下式 ( $k+1$ 用 $i$ 来表示)。 $$ i=i\&(\sim i+1) $$  正数 $i$ ( $i=k+1$ 大于等于1,必为正) 的相反数 $-i$ 必是负数,[我们知道](https://en.wikipedia.org/wiki/Signed_number_representations),负数在计算机中以补码 ([two's complement](https://en.wikipedia.org/wiki/Two%27s_complement)) 表示, **负数 $-i$ 的补码为对应正数 $i$ 的除符号位外按位取反后再加 1** ,即 $-i=\sim i+1$ ,恰好与上述式子与运算 $\&$ 的右边相同,于是我们给出如下 $lowbit(i)$方法,如其方法名所表达的那样, **该方法返回下标 $i$ 的二进制表示中的最低位的 1 所代表的数** 。后续我们可以用该方法方便地对当前子区间右界 $i$ 求其左界,即其左邻子区间右界 $i-lowbit(i)$ 。 ```java private int lowbit(int i){ return i & -i; } ``` 下图展示了大小为 16 的 $nums$ (图中的 $a$ 数组) 的子区间划分 ($t[]$ 为 $tree[]$ ),16个矩形代表划分出的16个子区间。如图,$tree[0]$ 表示右界为 $nums[0]$ 的区间和 (该区间只有一个元素),$tree[1]$ 表示右界为 $nums[1]$ 的区间的区间和 (该区间只有 $nums[0]$ 和 $nums[1]$ 两个元素),依次类推。蓝线表示 **区间包含关系** 。单点修改操作需要更新所有包含修改点的区间的区间和,寻找包含修改点的区间的过程就是 **沿着蓝线向上** 的过程。 到这里,相信读者们应该对「树状数组」和 「*Binary Indexed Tree*」有了更深的理解。 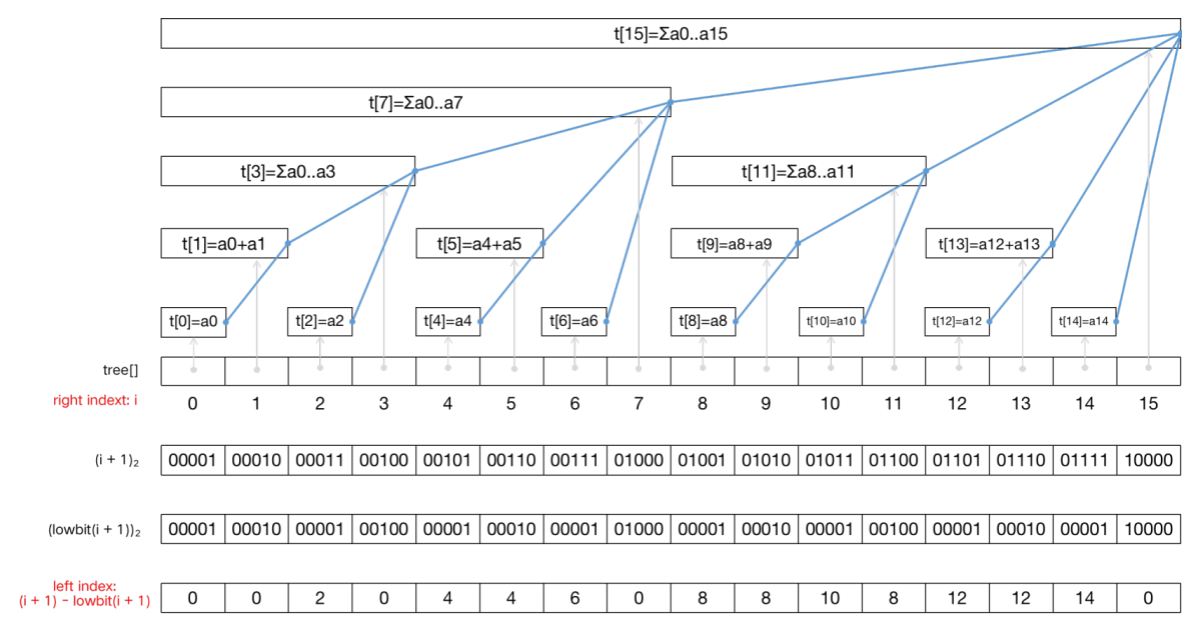 将该图稍作调整可以更清晰地看出「树」的结构。 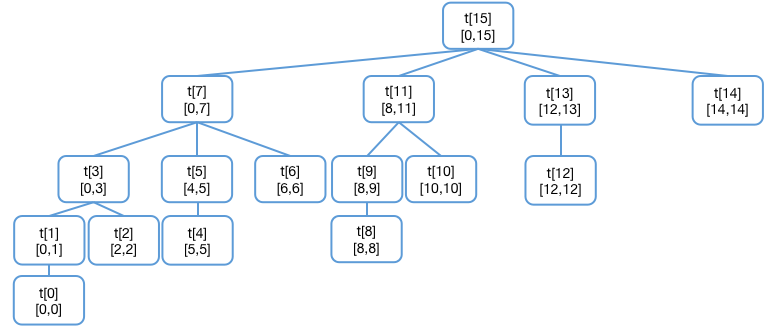 需要强调的是,$tree$ 所代表的逻辑树并非二叉树,英文名称中的 binary 指的是下标 **「二进制」表示中「二」** ,表达的是下标二进制数位取 0 或取 1 得到的下标值与 $tree$ 逻辑结点的索引关系。对于大小不是 2 的整数次幂的 $nums$ ,其子区间构成多棵而不是一棵多叉树。例如大小 $nums$ 大小为 15 时 ($[0,14]$),子区间构成四棵多叉树,分别以结点 $tree[7]$, $tree[11]$, $tree[13]$ , $tree[14]$ 为根结点。 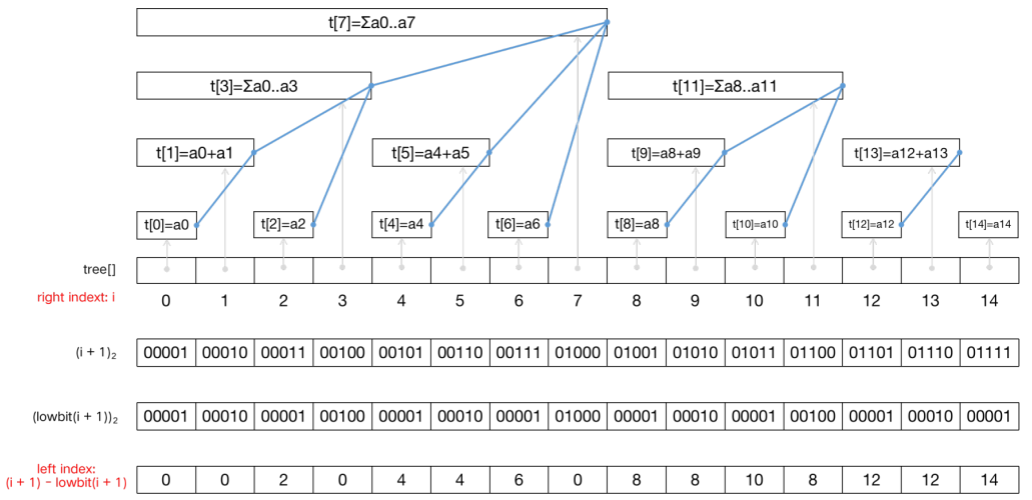 接下来我们分析如何实现「单点修改」和「区间查询」,分析过后你会知道之前需求 3 和 5 是如何被满足的。 <br /> #### 单点修改 更新 $nums[k]$ ,需要相应地更新包含它的所有区间的区间和 $tree[]$ 。通过前面的树状图,我们不难看到,**第一个要更新的区间和一定是 $tree[k]$** 。沿着蓝线上升,考虑蓝线连接的父子结点的下标二进制表示,我们发现 $i = i + lowbit(i)$ ($i=k+1$) 总是 (包含修改点的) 下一个更大的 (父结点) 区间的右界加 1 ,每上升一层,就会找到包含修改点的更大范围的区间。$i$ 的最大值是区间右界下标 $n-1$ 加 1,即 $nums$ 的大小 $n$ 。 增量式单点修改方法为 `public void add(int k, int x)` 表示为包含 $nums[k]$ 的所有区间和加上增量 $x$ 。该方法将从 $tree[k]$ 开始,沿着蓝色链条依次为包含 $nums[k]$ 的所有区间加上增量 $x$ 。可见 $add$ 方法的主体是一个循环,蓝色链条上的区间和结点下标 $i$ 的更新我们已经知道。 若单点修改为覆盖式修改,则执行 `public void update(int k, int x)` ,表示更新 `nums[k] = x` ,通过调用 `public void add(int k, int x)` 方法实现。于是不难写出如下 $update$ 和 $add$ 方法。寥寥数行,配合 $lowbit$ 向上更新,十分奇妙。 再次强调,$i$ 的取值总是当前区间右界下标加 1,因此更新区间和时下标为 $i-1$ (对应该区间右界下标),即 $tree[i-1]$ 。 ```java // 单点修改: 令 nums[k] = x public void update (int k, int x){ add(k, x - nums[k]); nums[k] = x; // 更新 nums[k] 为 x } // 单点修改: 令 nums[k] += x public void add(int k, int x){ for(int i = k + 1; i <= n; i += lowbit(i)){ tree[i - 1] += x; // 包含第 k 项的区间都加上 x } } ``` 下图展示了 $add(4,2)$ 的过程。 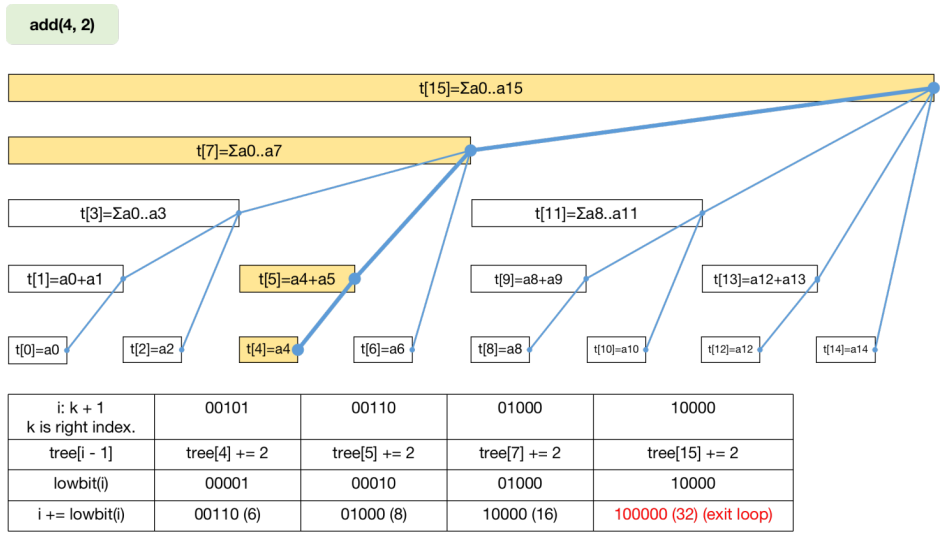 <br /> #### 区间查询 给定 $nums$ 上的区间 $[l,r]$ ,求区间和。利用前缀和的思想,我们定义方法 `private int preSum(int k)` ,表示求 $nums[0]$ 到 $nums[k]$ 的和 (前 $k+1$ 项和) ,那么求 $[l,r]$ 的区间和即为 $preSum(r) - preSum(l - 1)$ 。以求 $preSum(r)$ 为例,在「区间划分」中我们已经知道通过 `i = i - lowbit(i)` 的方式从 $i=r+1$ 开始依次求出组成 $[0,r]$ 区间的子区间的右界下标 ($i-1$),也即区间和逻辑结点 $tree$ 的下标,依次将得到的 $tree[i-1]$ 累计即可得到要求的前缀区间和。可见 `preSum(k)` 方法的主体是一循环,循环条件是 $i > 0$ ,循环终止时 ( $i==0$ ) 求出 $nums[0]$ 到 $nums[k]$ 的和,不难写出如下 $sum$ 和 $preSum$ 方法。 ```java // 区间查询 (区间求和): 求 nums[l] 到 nums[r] 之和 public int sum(int l, int r){ return preSum(r) - preSum(l - 1); } // 求前缀和: 求 nums[0] 到 nums[k] 的区间和 (前 k+1 项和) private int preSum(int k){ int ans = 0; for(int i = k + 1; i > 0; i -= lowbit(i)){ ans += tree[i - 1]; } return ans; } ``` 下图展示了 $preSum(14)$ 的过程。 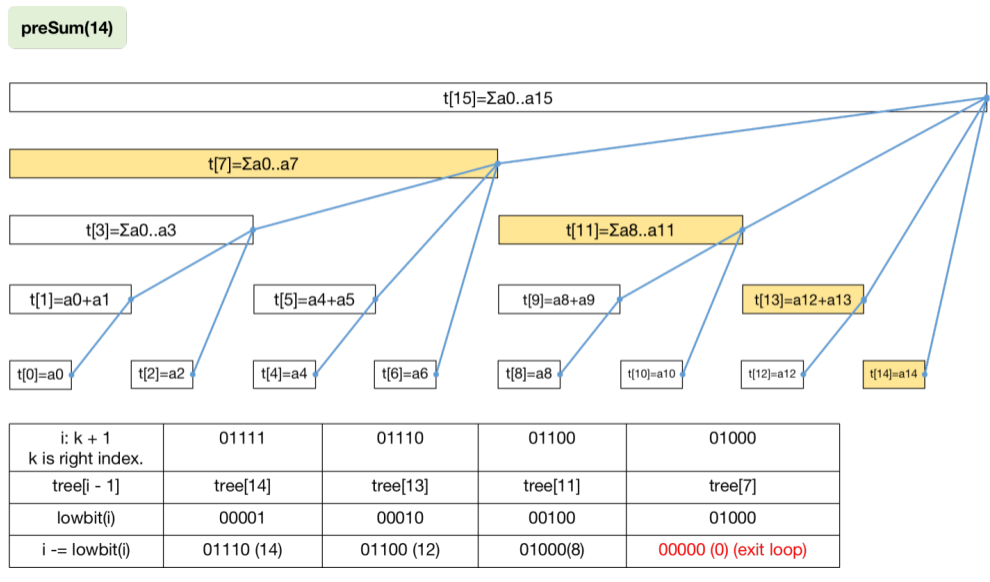 <br /> #### 初始化 从「区间划分」入手,我们得出了基本树状数组所要解决的单点修改和区间查询操作,这两种操作都要建立在最初 $tree[]$ 有值的情况下,现在我们回过头分析 $tree[]$ 的初始化。 一开始 $tree[]$ 所有元素值均为 0,前面我们说过,单点修改 $nums[i]$ 时,首个需要更新的结点的区间和为 $tree[i]$ ,调用 $add(i, nums[i])$ 方法,更新 $tree[i]$ 之后,$add$ 中的 $for$ 循环会沿着蓝色链条向上更新所有包含该修改点的更大的区间结点的区间和。因此, $tree[]$ 的初始化可以按 **任意顺序** 调用 $n$ 次 $add$ 初始化 $n$ 个区间的区间和,每次调用 $add$ 更新某个区间和时,总能保证受影响的更大区间的区间和得到更新。一般我们按 $0 \sim n-1$ 的顺序初始化 $tree$ (即按 $0 \sim n-1$ 的顺序调用 $add(i, nums[i])$ ),在树状数组类的实现中,初始化部分如下。 ```java // 单点修改区间查询 class PURQBIT { int[] nums, tree; // nums 为输入数组,tree 为对应 nums 的区间和树状数组 int n; // nums大小 public PURQBIT(int[] nums){ this.nums = nums; this.n = nums.length; this.tree = new int[n]; for(int i = 0; i < n; i++){ add(i, nums[i]); } } } ``` <br /> #### 时空复杂度 **时间复杂度:** 1. **单点修改时间复杂度** : $O(logn)$ 。 取决于更新结点到根结点的路径上的结点数,更新 $nums[0](k=0)$ 时路径上结点数最多,其数量为 $i=k+1$ 从 $(000...001)_2$ 通过 $i += lowbit(i)$ 逐位更新到 $(n)_2$ 的更新次数。该数量不会大于 $(n)_2$ 的位数,也即 $logn$ ,因此单点修改的时间复杂度为 $O(logn)$。 2. **区间查询时间复杂度** : $O(logn)$ 。 区间为 $[l, r]$, $[0,l-1]$ 与 $[0,r]$ 的连续子区间个数分别为 $p, q$ 个,则区间查询复杂度取决于 $max(p,q)$ 。根据子区间界的计算方法,子区间个数与 $i$ 的二进制数中 1 的数量有关 ( $i$ 为区间右界 $k$ 加 1,$i=k+1$ ),假设 $i$ 的二进制数有 $t$ 位,则 $i=2^t-1$ 时 1 的位数最多,共 $t$ 个, $t=log(i+1)$。根据 $sum$ 方法,要求 $[0,l-1]$ 以及 $[0,r]$ 的前缀区间和,时间复杂度为 $O(2*t)$ 。故区间查询的时间复杂度为 $O(logn)$。 3. **初始化时间复杂度** : 调用 $n$ 次 $add$ ,时间复杂度为 $O(nlogn)$ 。 **空间复杂度:** $O(n)$ ,即 $tree$ 数组大小 $n$ 。 <br /> #### 类的实现代码 以下是「基本树状数组」 (PURQ BIT) 的实现代码,所有方法均已分析。「实战应用」中给出的 [307. 区域和检索 - 数组可修改](https://leetcode.cn/problems/range-sum-query-mutable/) 是基本树状数组 (PURQ BIT) 模版题,利用我们给出的代码可轻松解决,详细可参考 [题解](https://leetcode.cn/problems/range-sum-query-mutable/solution/yukiyama-by-yukiyama-euo5/) 。 在这里对 $tree$ 的下标范围做一个特别说明。最早给出的实现代码中,采用的是 $tree$ 大小为 $n+1$ 的实现,即 $tree[i]$ 为以 $nums[i-1]$ 为右界的子区间的区间和。但后来感觉还是让 $tree$ 与 $nums$ 完全对齐会更方便理解,即 $tree[i]$ 为以 $nums[i]$ 为右界的子区间的区间和,毕竟下标总是加一减一多少会带来一些思考负担。 ```java // 单点修改区间查询 class PURQBIT { int[] nums, tree; // nums 为输入数组,tree 为对应 nums 的区间和树状数组 int n; // nums大小 public PURQBIT(int[] nums){ this.nums = nums; this.n = nums.length; this.tree = new int[n]; for(int i = 0; i < n; i++){ add(i, nums[i]); } } // 单点修改: 令 nums[k] = x public void update (int k, int x){ add(k, x - nums[k]); nums[k] = x; // 更新 nums[k] 为 x } // 单点修改: 令 nums[k] += x public void add(int k, int x){ for(int i = k + 1; i <= n; i += lowbit(i)){ tree[i - 1] += x; // 包含第 k 项的区间都加上 x } } // 区间查询 (区间求和): 求 nums[l] 到 nums[r] 之和 public int sum(int l, int r){ return preSum(r) - preSum(l - 1); } // 求前缀和: 求 nums[0] 到 nums[k] 的区间和 (前 k+1 项和) private int preSum(int k){ int ans = 0; for(int i = k + 1; i > 0; i -= lowbit(i)){ ans += tree[i - 1]; } return ans; } private int lowbit(int i){ return i & -i; } } ``` <br /> ### RUPQ BIT (区改单查) 基本树状数组 (PURQ BIT) 很好地支持了「单点修改」及「区间查询」操作。我们进一步思考更多的区间操作,例如 **「区间修改」** 操作,即将指定区间的每一个元素都加上同一个值,也叫「增量式区间修改」,如果仍用基本树状数组,我们只能对区间内的每一个元素都执行一次单点修改来实现,这显然不是我们想要的。接下来我们介绍的 RUPQ BIT 引入差分数组 $diff[]$ ,使得 **「区间修改」** 和 **「单点查询」** 操作的时间复杂度均为 $O(logn)$ 。 <br /> #### 差分数组 「RUPQ BIT」实现的关键是 **「差分数组」** 。对大小为 $n$ 的输入数组 $nums$ ,对应的差分数组 $diff$ 为: $$ \begin{aligned} diff[0] &=nums[0] \\ diff[i] &= nums[i] - nums[i - 1] (i>0) \end{aligned} $$ 下面我们指出关于差分数组的重要性质。 1. **区间修改** : $[l, r]$ 区间每个元素加 $x$ 。根据 $diff$ 的定义,除了 $diff[l] += x$ 、$diff[r+1] -= x$ 外,其他 $diff$ 元素值不变。因为若两个作差的元素都增加了 $x$ ,则差值不变。 2. **单点查询** : 由于我们不修改 $nums$ 的元素 (否则时间复杂度为 $O(n)$ ),因此区间修改后,我们将无法再通过 $nums$ 来查询单个元素值。但通过下式,我们有 $nums[k] = \sum_{i=0}^{k} diff[i]$,也就是 $diff[0]$ 到 $diff[k]$ 的和 (前缀和) 为 $nums[k]$ 。 $$ \begin{aligned} nums[k] &=(nums[k]-nums[k-1])+(nums[k-1]-nums[k-2])+...+ \\ &\quad (nums[1]-nums[0])+nums[0] \\ &= diff[k]+diff[k - 1]+...+diff[1]+diff[0] \end{aligned} $$ 对于「单点查询」,例如 $nums = \{4,2,-2,7,8\}$,则 $diff =\{4,-2,-4,9,1\}$ 。我们对先对 $[1,3]$ 区间加 3,然后再求 $nums[2]$ 。 | 操作 | nums | diff | | ---------------- | ------------------------------------------ | ----------------- | | 初始 | $\{4,2,-2,7,8\}$ | $\{4,-2,-4,9,1\}$ | | $[1,3]$ 区间加 3 | $\{4,5,1,10,8\}$ <br />※ 实际不修改 $nums$ | $\{4,1,-4,9,-2\}$ | 对照上表与前述分析,可以看到 $diff[]$ 中除了 $diff[1]+=3$ 及 $diff[4]-=3$ ,其他不变。且 $nums[2]=diff[0]+diff[1]+diff[2]=1$ ,通过求 $diff$ 前缀和完成了单点查询。因此,借助「差分数组」,对 $nums$ 的区间修改实际可以通过对 $diff$ 执行两次 **单点修改** 来表达,时间复杂度为 $O(1)$ ,而对 $nums$ 的单点查询实际上是对 $diff$ 的 **区间查询 (求前缀区间和)** , 时间复杂度为 $O(n)$ 。 如果把 $diff[]$ 数组看作 PURQ BIT 中的 $nums[]$ ,那么对原输入序列 $nums[]$ 的 **区间修改** ,可通过单点修改 $diff[l]$ 和 $diff[r+1]$ 来表达,对应了 PURQ BIT 中的 $add$ 操作。对原输入序列 $nums[]$ 的 **单点查询** 则对应基本 BIT 中的求前缀和的 $preSum$ 操作。下面我们分析 RUPQ BIT,并给出实现。 <br /> #### 从PURQ到RUPQ 经过前述分析,快速理解 RUPQ BIT 的关键只需明确一点: RUPQ BIT 中的 $tree[]$ 对应的是 $diff[]$ 的所有子区间的区间和。如下是 PURQ BIT 和 RUPQ BIT 的简单对比。 | | PURQ BIT | RUPQ BIT | | -------------- | ------------------------------------------ | ------------------------------------------ | | 输入数组 | $nums[]$ | $nums[]$ | | 前缀和求解对象 | $nums[]$ | $diff[]$ | | 逻辑二元索引树 | $nums[]$ 的所有子区间的区间和构成 $tree[]$ | $diff[]$ 的所有子区间的区间和构成 $tree[]$ | 通过「差分数组」的学习,我们知道 RUPQ BIT 的「区间修改」,实际上只需要执行 $add(l, x)$ 以及 $add(r+1,-x)$ 。我们已经知道,$add$ 方法中的 $for$ 循环会沿着结点的父链不断更新更大区间的区间和。这一点保证了「单点查询」时, 执行 $preSum(k)$ 能够取得正确的 $diff[0] \sim diff[k]$ 的和,也就是 $nums[k]$ 。除了初始时需要从 $nums$ 求出 $diff$ ,RUPQ BIT 的 $add$ 和 $query$ 方法与 PURQ BIT 是完全相同的。 <br /> #### 时空复杂度 分析方法及结果均同 PURQ BIT。 <br /> #### 类的代码实现 以下是 RUPQ BIT 的实现代码。「实战应用」中给出的 [307. 区域和检索 - 数组可修改](https://leetcode.cn/problems/range-sum-query-mutable/) 虽是基本树状数组 (PURQ BIT) 模版题,但我们也可以用 RUPQ BIT 解决。用左右界相同的区间修改来实现单点修改,对区间大小为 $k$ 的区间求和,执行 $k$ 次单点查询并累加来实现区间求和。当然,后者的时间复杂度为 $O(nlogn)$ ,比维护 $nums$ 并在其上直接累加 $k$ 个元素来实现区间求和还要糟糕,不过我们只是为了验证此处给出的 RUPQ BIT 的正确性,虽然超时,但不报错,说明我们给出的实现是正确的。详细可参考 [题解](https://leetcode.cn/problems/range-sum-query-mutable/solution/yukiyama-by-yukiyama-euo5/) 。 ```java // 区间修改单点查询 class RUPQBIT { int[] diff, tree; // diff 为差分数组,tree 为对应 diff 的树状数组 int n; public RUPQBIT(int[] nums){ // nums 为输入数组 this.n = nums.length; // 有效元素个数 this.diff = new int[n]; this.tree = new int[n]; diff[0] = nums[0]; // 求diff[] for(int i = 1; i < n; i++){ // 求 diff[] diff[i] = nums[i] - nums[i - 1]; } for(int i = 0; i < n; i++){ // 初始化 tree[] add(i, diff[i]); } } // 区间修改: nums[l] 到 nums[r] 所有元素加上 x // --> 实际单点修改 diff[l] 和 diff[r + 1] public void update(int l, int r, int x){ add(l, x); add(r + 1, -x); } // 单点查询: nums[k] // --> 实际求 diff 的前缀区间和 ([0, k]) public int query(int k){ return preSum(k); } // 单点修改: 令 diff[k] += x private void add(int k, int x){ for(int i = k + 1; i <= n; i += lowbit(i)){ tree[i - 1] += x; // 包含第 k 项的区间都加上 x } } // 求前缀和: 求 diff[0] 到 diff[k] 的区间和 (前 k+1 项和) private int preSum(int k){ int ans = 0; for(int i = k + 1; i > 0; i -= lowbit(i)){ ans += tree[i - 1]; } return ans; } private int lowbit(int i){ return i & -i; } } ``` 我们已经有了 PURQ BIT ,因此 RUPQ BIT 可以十分简单地调用前者的方法即可,所以 RUPQ BIT 类也可以这么写。 ```java // 区间修改单点查询 class RUPQBIT2 { private PURQBIT purqBit; public RUPQBIT2(int[] nums){ // nums 为输入数组 int[] diff = new int[nums.length]; diff[0] = nums[0]; // 求diff[] for(int i = 1; i < nums.length; i++){ // 求 diff[] diff[i] = nums[i] - nums[i - 1]; } this.purqBit = new PURQBIT(diff); } // 区间修改: nums[l] 到 nums[r] 所有元素加上 x // --> 实际单点修改 diff[l] 和 diff[r + 1] public void update(int l, int r, int x){ purqBit.add(l, x); purqBit.add(r + 1, -x); } // 单点查询: nums[k] // --> 实际求 diff 的前缀区间和 ([0, k]) public int query(int k){ return purqBit.sum(0, k); } } ``` <br /> ### RURQ BIT (区改区查) 本小节介绍第三种树状数组,RURQ BIT ,即 **「区间修改区间查询」树状数组** 。RURQ BIT 以 $O(logn)$ 时间复杂度支持 **「区间修改」** 及 **「区间查询」** 。 <br /> #### 从RUPQ到RURQ 该版本的 BIT 在 RUPQ BIT 差分数组的基础上, 通过如下算式推导发现只需 **再引入一棵逻辑树** 即可同时以 $O(logn)$ 时间复杂度实现 **「区间修改」** 及 **「区间查询」** 。 $$ \begin{aligned} sum(l,r) &= preSum(r)-preSum(l-1) \\ &= (nums[0]+nums[1]+,...,+nums[r])-(nums[0]+nums[1]+...+nums[l-1]) \\ \end{aligned} $$ $$ \begin{aligned} preSum(k)&=nums[0]+nums[1]+,...,+nums[k] \\ &=diff[0]+(diff[0]+diff[1])+,...,+(diff[0]+diff[1]+,...,+diff[k])\\ &=(k+1)*diff[0]+k*diff[1]+,...,+diff[k] \\ &=(k+1)*(diff[0]+diff[1]+,...,+diff[k])\\ &\quad -(0*diff[0]+1*diff[1]+,...,+k*diff[k]) \end{aligned} $$ 从 $preSum(k)$ 的推导的最后一行可以看到,减号左边是 $k+1$ 倍的 $preSum(k)$ (RUPQ BIT),而右边可以引入新的逻辑树数组 $helperTree$ 来维护数组 $helperArr=\{i*diff[i]\}, i∈[0,n-1]$ 的区间和,每次区间修改时,同时修改 $tree, helperTree$ ,如此,便可通过上面给出的式子实现「区间查询」。具体实现请看「类的实现代码」。 <br /> #### 时空复杂度 分析方法及结果类似 PURQ BIT。 <br /> #### 类的实现代码 以下是 RURQ BIT 的实现代码。「实战应用」中给出的 [307. 区域和检索 - 数组可修改](https://leetcode.cn/problems/range-sum-query-mutable/) 虽是基本树状数组 (PURQ BIT) 模版题,但我们也可以用 RURQ BIT 解决。其中,单点修改用左右界相同的区间修改来实现,通过 RURQ BIT 实现的 PU / RQ 操作的时间复杂度也都是 $O(logn)$。详细可参考 [题解](https://leetcode.cn/problems/range-sum-query-mutable/solution/yukiyama-by-yukiyama-euo5/) 。 ```java // 区间修改区间查询 class RURQBIT { int[] diff, tree, helperTree; int n; public RURQBIT(int[] nums){ this.n = nums.length; // 有效元素个数 this.diff = new int[n]; this.tree = new int[n]; this.helperTree = new int[n]; diff[0] = nums[0]; // 求diff[] for(int i = 1; i < n; i++){ // 求 diff[] diff[i] = nums[i] - nums[i - 1]; } for(int i = 0; i < n; i++){ // 初始化 tree[] 和 helperTree[] add(tree, i, diff[i]); add(helperTree, i, i * diff[i]); } } // 区间修改: nums[l] 到 nums[r] 所有元素加上 x // --> 实际单点修改 diff[l], diff[r + 1] 及对应的 l * diff[l], (r + 1) * diff[r + 1] public void update(int l, int r, int x){ add(tree, l, x); add(tree, r + 1, -x); add(helperTree, l, l * x); add(helperTree, r + 1, (r + 1) * (-x)); } // 区间查询 (区间求和): 求 nums[l] 到 nums[r] 之和 // --> 实际求两次前缀和后作差 public int sum(int l, int r){ int preSumLeft = l * preSum(tree, l - 1) - preSum(helperTree, l - 1); int preSumRight = (r + 1) * preSum(tree, r) - preSum(helperTree, r); return preSumRight - preSumLeft; } // 求前缀和: 求 thisTree 对应的序列的 [0, k] 前缀区间之和 public int preSum(int[] thisTree, int k){ int ans = 0; for(int i = k + 1; i > 0; i -= lowbit(i)){ ans += thisTree[i - 1]; } return ans; } // 单点修改: 为 thisTree 对应的序列下标为 k 的元素加上 x private void add(int[] thisTree, int k, int x){ for(int i = k + 1; i <= n; i += lowbit(i)){ thisTree[i - 1] += x; // 包含下标为 k 的项的区间都加上 x } } private int lowbit(int i){ return i & -i; } } ``` <br /> ### 离散化 对于区间问题,当我们只关心输入数组 $nums$ 元素的大小关系而不关心元素的具体值时,为了压缩空间,我们先将 $nums$ 离散化。常见的离散化方式有两种,它们都基于排序,但其中一种借助了 $set$ 去重,使得离散化后的有效数字更少,取值范围更小,我把这种方式称为 **「紧离散」** ;另一种则没有去重,因此离散化后的有效数字更多 (存在相同的数字),取值范围也更大,我称之为 **「松离散」** 。以下是两种离散化方式的实现。 **松离散** ```java // 松离散方法 private void discrete(int[] nums){ int n = nums.length; int[] tmp = new int[n]; System.arraycopy(nums, 0, tmp, 0, n); Arrays.sort(tmp); for (int i = 0; i < n; ++i) { nums[i] = Arrays.binarySearch(tmp, nums[i]) + 1; } } ``` **紧离散** ```java // 紧离散方法 private Map<Integer, Integer> discrete(int[] nums){ Map<Integer, Integer> map = new HashMap<>(); Set<Integer> set = new HashSet<>(); for(int num : nums) set.add(num); List<Integer> list = new ArrayList<>(set); Collections.sort(list); int idx = 0; for(int num : list) map.put(num, ++idx); return map; } ``` 例如对于 $nums=\{2,4,4,6\}$ ,松离散得到 $nums=\{1,2,2,4\}$,离散化后的 $nums$ 大小与原来相同;紧离散得到 $map=\{(2,1),(4,2),(6,3)\}$ , $key$ 为 $nums$ 中的元素,对应的 $value$ 为其离散化值,$value$ 一定是从 1 开始的没有重复的连续正整数。两种方式离散化后虽然有效数字不同,取值范围也不同,但求解结果都是正确的 (读者可以思考一下为什么)。松离散无需哈希计算,通常速度更快,但有的题目可能更适合返回 $map$ 的紧离散 (例如 [327. 区间和的个数](https://leetcode.cn/problems/count-of-range-sum/) 和 [493. 翻转对](https://leetcode.cn/problems/reverse-pairs/) )。 <br /> ### 指定区间内指定取值范围的元素数 下面我们重点介绍巧用树状数组解决的一类常见问题 ── **求指定区间 $[l,r]$ 内大小在指定取值范围 $[lower, upper]$ 内的元素数** 。 有点拗口?没关系,我们先从著名的 **「逆序对」** 问题开始。 [剑指 Offer 51. 数组中的逆序对](https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/) 一题,求输入数组 $nums$ 的逆序对, **是树状数组的经典应用,更是一个「妙用」** 。我们指出,它属于本节标题「指定区间指定取值范围的元素数」的范畴。 但在讨论树状数组解法之前,我们先给出最朴素两层循环做法 (该做法有许多不同的写法,这里选取一种与我们树状数组解法最为对应的写法)。 - 外层循环遍历 $nums$ ,对于当前元素 $nums[i]$ ,内层循环 **顺序遍历** $nums[j](j>i)$ ,如果 $nums[i]>nums[j]$ ,则 $(nums[i],num[j])$ 是一个逆序对,令 $countGreater[j]++$ , $countGreater[j]$ 表示 $nums[j]$ 与其左侧的数形成的逆序对的个数。 - 当程序结束时,每一个 $countGreater[i]$ 就是 $nums[i]$ 的逆序数 (逆序对形式为 $(x,nums[i]),x>nums[i]$ ,$x$ 是 $nums[i]$ 左侧的元素),累计所有的 $countGreater[i]$ 就是所要求的 $nums$ 的逆序对总数。由于 $countGreater[i]$ 是在结束针对d $nums[i-1]$ 的内层循环时确定的,因此在开始 $nums[i]$ 内层循环前累计。 ```java class Solution { public int reversePairs(int[] nums) { int n = nums.length, ans = 0; int[] countGreater = new int[n]; for(int i = 0; i < n; i++){ ans += countGreater[i]; for(int j = i + 1; j < n; j++){ if(nums[i] > nums[j]) countGreater[j]++; } } return ans; } } ``` 我们再回到树状数组的做法,如下。其中的 $discrete$ 是「离散化」一节给出的「松离散」方法,BIT 类是我们在前面给出的 PURQ BIT 类 (该题详细 [题解](https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/by-yukiyama-elnl/) )。 ```java class Solution { public int reversePairs(int[] nums) { discrete(nums); // 松离散 BIT bit = new BIT(nums); int n = nums.length, ans = 0; for(int i = n - 1; i >= 0; --i) { ans += bit.preSum((nums[i] - 1) - 1); bit.add(nums[i] - 1, 1); } return ans; } } ``` 在主方法 $reversePairs$ 中,首先将 $nums$ 离散化 (后续的 $nums$ 均指离散化后的 $nums$ ) ,接着 **逆序遍历** $nums$ 元素,对每一个 $nums[i]$ ,依次执行 $preSum$ 和 $add$ 方法。我们知道 $preSum(k)$ 是求输入序列前 $k+1$ 项的和,$add(k,x)$ 是从首个包含下标为 $k$ 的元素的区间开始,为所有包含该元素的区间的区间和加上 $x$ 。那么代码中的 $add(nums[i]-1,1)$ 是什么意思呢?对比朴素做法,可知 $add(nums[i]-1,1)$ 相当于朴素做法的内层循环,用于计算「当前元素逆序数」,分析如下。 该方法使得 $tree$ 从 $tree[nums[i]-1]$ 开始,沿着父链上升,包含下标为 $nums[i]-1$ 的更大区间 $x$ 的 $tree[x]$ 加 1 。$tree$ 的下标范围 $[0,n-1]$ 与 (松离散化后的) $nums$ 元素值的大小范围 $[1,n]$ **一一对应** ,可以把 $add$ 方法 (以及 $preSum$ 方法) 中的 $nums[i]-1$ 等同于原数组中的 $nums[i]$ 方便理解。 $tree[i]$ 的意义也不再是区间和。 举例说明。假设松离散化后有 $nums = \{2,6,8,7,4,5,1,3\}$ ,逆序遍历 $nums[i]$ 并执行 $add(nums[i]-1,1)$ 。对第一个遍历到的 $nums[7]=3$ 执行 $add(2, 1)$ (操作 ① ),如下图。 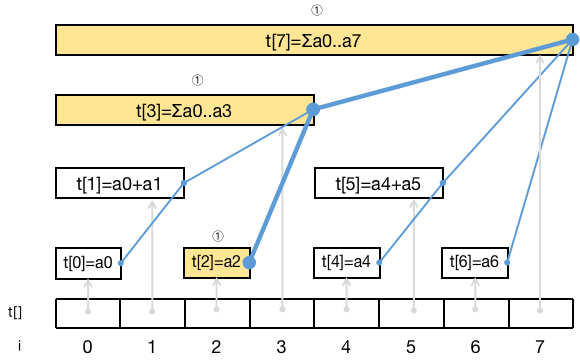 $add$ 操作使得 $tree[2]$ , $tree[3]$ , $tree[7]$ 增加 1 ,其意义相当于为数组中 **大于等于** $nums[7]$ 的所有数 $nums[j]$ ,都执行 $countGreaterEqual[j]++$ 。注意,树状数组做法中不存在 $countGreaterEqual$ ,这里只是类比朴素方法中的 $CounterGreater$ 数组。那我们如何得到此时的 $countGreaterEqual[j]$ 呢?从代码中我们已经知道,通过执行 $preSum$ 方法求得。 由于我们从后往前求逆序对,因此我们考察左侧元素 $nums[j]$ 的 $countGreaterEqual[j]$ (不存在该数组,只是类比) 是否被正确更新了。由上图很容易看出,可通过 $preSum(nums[j]-1)$ 查询到。 ``` preSum(nums[6] - 1) = preSum[0] = 0 preSum(nums[5] - 1) = preSum[4] = 1 preSum(nums[4] - 1) = preSum[3] = 1 preSum(nums[3] - 1) = preSum[6] = 1 preSum(nums[2] - 1) = preSum[7] = 1 preSum(nums[1] - 1) = preSum[5] = 1 preSum(nums[0] - 1) = preSum[1] = 0 ``` 所以本质上 $add(nums[i]-1,1)$ 操作相当于对 $nums$ 中的 **大于等于** $nums[i]$ 的所有的 $nums[j]$ ,使其对应的 $countGreaterEqual[j]$ 加 1 。而 $counterGreaterEqual[j]$ 是通过 $preSum(nums[j]-1)$ 求得的。遍历 $nums[i]$ 时,以它为逆序对左元素 (即 $(nums[i], x)$ 形式,$x$ 是 $nums[i]$ 右侧的元素) 的逆序对数量在上一轮执行 $add[nums[i-1] - 1, 1]$ 后就完全确定了,因此先执行 $preSum$ 方法累计该逆序对数。 需要注意的是,当我们执行 $preSum(nums[i]-1)$ 时,求的是 $\{(nums[i],x), nums[i]≥x\}$ 的数量 (对应 $counterGreaterEqual[i]$),而逆序对要求的是 $\{(nums[i],x), nums[i]>x\}$ (对应 $counterGreater[i]$) ,即严格大于才算逆序。要如何处理呢?再次看向树状图,以 $preSum(6)$ 为例,其结果为 $tree[6]+tree[5]+tree[3]$ ,其中 $tree[6]$ 就代表了等于时带来的累计量,去掉这个累计量只需要向左侧移动一位即可,即求 $preSum(5)$ 。对应到题解代码中,即为 $preSum((nums[i]-1)-1)$ ,或写成 $preSum(nums[i]-2)$ ,对应了朴素解法中的 $counterGreater[i]$ 。 现在我们将树状数组解法与朴素解法对比如下。 | 操作 | 朴素解法 | 树状数组解法 | | -------------------- | ------------------------------------------------------------ | ------------------------------------------------------------ | | 累计当前元素的逆序数 | `ans += countGreater[i];`<br />$(x,nums[i]),x>nums[i]$ 形式逆序对 | `ans += bit.preSum(nums[i] - 2);`<br />$(nums[i],x),nums[i]>x$ 形式逆序对 | | 计算当前元素的逆序数 | 内层循环<br />$(nums[i],x),nums[i]>x$ 形式逆序对 | `bit.add(nums[i] - 1, 1);`<br />$(x,nums[i]),x>nums[i]$ 形式逆序对 | 我们惊讶地发现,$add$ 方法本质上完成了朴素做法的内层循环所做的事,并且是以 $O(logn)$ 时间复杂度完成的。而且实际上完成得更多,因为朴素做法更新的是 $nums[i]$ 右侧的小于 $nums[i]$ 的 $nums[j] (j>i)$ 的 $countGreater[j]$ ,而树状数组 $add$ 方法是对所有大于等于 $nums[i]$ 的 $nums[j]$ 更新其 $countGreaterEqual[j]$ (类比,实际通过 $preSum(num[j]-1)$ 求出),并不限制在 $nums[i]$「左侧」,只不过我们按逆序方向执行 (向左处理),即便 $nums[i]$ 右侧某个元素大于 $nums[i]$ ,经由 $add$ 方法使该数对应的逆序数增加 1,它也没有机会再被累加了,况且,它在 $nums[i]$ 右侧,与 $nums[i]$ 构成的实际上是正序对。 总之,我们将一个 $nums$ 离散化后,逆序遍历它,先执行 $preSum(nums[i]-2)$ ,这个操作即为获取 $\{(nums[i],x),nums[i]>x\}$ 形式的逆序对对数。再执行 $add(nums[i]-1, 1)$ 找到 $\{(x,nums[i]),x>nums[i]\}$ 形式的逆序对,更新相应的 $tree[]$ 值。 实际上 $preSum(([nums[i]-1)-1])$ 就是本小节标题「指定区间内指定取值范围的元素数」 的体现。即执行 $preSum((nums[i]-1)-1)$ 时,查询 $[i+1,n-1]$ 区间取值范围为 $[1,nums[i]-1]$ 的数的数量 (即 $\{(nums[i],nums[j]),j∈[i+1,n-1]\}$ 逆序对的数量)。 对于前面的例子 $nums = \{2,6,8,7,4,5,1,3\}$ ,我们给出执行 ① ~ ⑧ 后得到的树形图,供读者仔细验证。 ``` ① add(2, 1) ② add(0, 1) ③ add(4, 1) ④ add(3, 1) ⑤ add(6, 1) ⑥ add(7, 1) ⑦ add(5, 1) ⑧ add(1, 1) ``` 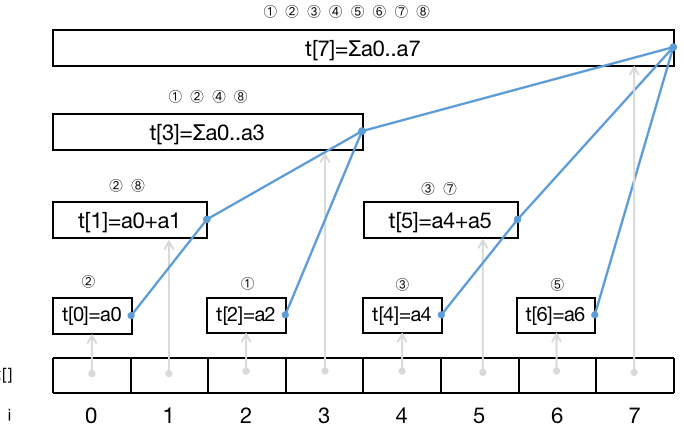 在理解了「遍历离散化后的 $nums$ ,在遍历过程中执行 $preSum$ 及 $add$ 」的意义后,类似的题目如下: - [315. 计算右侧小于当前元素的个数](https://leetcode.cn/problems/count-of-smaller-numbers-after-self/) 题,与「逆序数」问题的区别仅在此题要求解「小于」,逆序数问题中涉及的是「小于等于」,只需要在「小于等于」版本的代码上做简单调整即可,详情见题解。 - [406. 根据身高重建队列](https://leetcode.cn/problems/queue-reconstruction-by-height/) 也是用树状数组求对于当前元素它之前的「小于等于」它的元素个数的问题,具体实现需结合二分查找,这是树状数组与其他方法相结合的一个好例子。 - [493. 翻转对](https://leetcode.cn/problems/reverse-pairs/) 。「逆序对」的变形题,$query(x)$ 中 $x$ 的范围超过了离散化后 $nums$ 的取值范围,这一点类似 327 题,可能会被查询的数值要与原 $nums$ 中的数一起离散化。 - [327. 区间和的个数](https://leetcode.cn/problems/count-of-range-sum/) 。此题是更进阶的题目,不仅求解对象从 $nums$ 变成了 $preSums$ ,$lower, upper$ 的范围也不再是 $[1,n]$ ($n$ 是 $nums$ 的大小) 。这道题细节处理较多,详细内容请看题解。 不得不说树状数组的这个应用确实十分抽象,希望读者仔细阅读本节内容后能够完全理解。关于这几题的详细题解和更多的树状数组题目,请参考「实战应用」。 <br /> ### 总结 关于「树状数组」,总结本文内容如下。 1. 基本的树状数组 (PURQ BIT) 以 $O(logn)$ 时间复杂度解决长度为 $n$ 的序列的 **单点修改** 及 **区间查询** 问题。 2. 我们从区间查询出发,思考如何利用类似倍增思想的做法来划分子区间,从而提高区间查询的效率。 3. 通过对 $nums$ 下标二进制形式的观察,找到了一种将输入序列划分为 $n$ 个子区间的方式。链接子区间及包含它的更大一点的子区间后,这些子区间构成一棵或多棵逻辑上的多叉的 **「二元索引树」** 。 4. 单点修改及区间查询的时间复杂度都与 $(n)_2$ 的位数相关,简单分析后可知它们都是时间为 $O(logn)$ 的操作。 5. 在 PURQ BIT 的基础上,引入 **差分数组** ,实现了 RUPQ BIT。 6. 在 RUPQ BIT 的基础上,根据 **算式推导** ,引入 **辅助树状数组** ,实现了 RURQ BIT。 7. 当区间问题只关心元素之间的大小关系而不关心元素值时,可以先将输入序列 **离散化** ,有助于提高求解效率或帮助解决一些特定问题。离散化实现包括 **松离散** 和 **紧离散** 。 8. 「求指定区间 $[l,r]$ 内大小在指定取值范围 $[lower, upper]$ 内的元素数」是一类特定的可用树状数组巧妙解决的问题。 总结不同方式的 PU/PQ/RU/RQ 操作的时间复杂度如下。 | 方式 | 单点修改 | 单点查询 | 区间修改 | 区间查询 | | ------------------- | ----------- | ----------- | ----------- | ----------- | | 普通数组 | $O(1)$ | $O(1)$ | $O(n)$ | $O(n)$ | | 普通数组+前缀和数组 | $O(n)$ | $O(1)$ | $O(n)$ | $O(1)$ | | 差分数组 | $O(1)$ | $O(n)$ | $O(1)$ | $O(n)$ | | PURQ BIT | ★ $O(logn)$ | | | ★ $O(logn)$ | | RUPQ BIT | | ★ $O(logn)$ | ★ $O(logn)$ | | | RURQ BIT | | | ★ $O(logn)$ | ★ $O(logn)$ | 值得注意的是,RURQ BIT 对大小为1的区间执行区间修改和区间查询实际上就是单点修改和单点查询,因此 RURQ BIT 以 $O(logn)$ 复杂度同时实现了 单点修改 / 单点查询 / 区间修改(增量式) / 区间查询(区间求和) 操作。 <br /> ### 实战应用 | 题目 | 难度 | 题解 | | ------------------------------------------------------------ | ---- | ------------------------------------------------------------ | | [307. 区域和检索 - 数组可修改](https://leetcode.cn/problems/range-sum-query-mutable/)<br />※ PURQBIT模版题 | 中等 | [题解](https://leetcode.cn/problems/range-sum-query-mutable/solution/yukiyama-by-yukiyama-euo5/) | | [剑指 Offer 51. 数组中的逆序对](https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/) | 困难 | [题解](https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/by-yukiyama-elnl/) | | [315. 计算右侧小于当前元素的个数](https://leetcode.cn/problems/count-of-smaller-numbers-after-self/) | 困难 | [题解](https://leetcode.cn/problems/count-of-smaller-numbers-after-self/solution/yukiyama-by-yukiyama-nqas/) | | [406. 根据身高重建队列](https://leetcode.cn/problems/queue-reconstruction-by-height/) | 中等 | [题解](https://leetcode.cn/problems/queue-reconstruction-by-height/solution/yukiyama-shu-zhuang-shu-zu-er-fen-by-yuk-1ovu/) | | [493. 翻转对](https://leetcode.cn/problems/reverse-pairs/) | 困难 | [题解](https://leetcode.cn/problems/reverse-pairs/solution/by-yukiyama-ljyp/) | | [327. 区间和的个数](https://leetcode.cn/problems/count-of-range-sum/) | 困难 | [题解](https://leetcode.cn/problems/count-of-range-sum/solution/by-yukiyama-e9on/) | <br /> *** 【文章更新日志】 [2022-10-03] - 修改了目录结构。 [2022-09-23] - 文章开头新增若干介绍文字。 [2022-07-25] - [@isuxiz](/u/isuxiz/) (isuxiz) 指出一处笔误,感谢 🙏。 *** 图论算法从入门到放下 十大排序从入门到入赘