浅谈迷宫搜索类的双向bfs问题(例题解析)

agile Posted on Jul 13 2023

数据结构与算法

@[TOC](文章目录)
## 前言
>文章若有疏忽还请指正，更多精彩还请关注公众号：`bigsai`
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200215000450177.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwNjkzMTcx,size_16,color_FFFFFF,t_70)

在搜索问题中，以迷宫问题最具有代表性，无论是八皇后的回溯问题，还是dfs找出口，bfs找最短次数等等题目的问题。在我们刚开始ac的时候、可能有着很多满足感！感觉是个迷宫问题咱么都可以给他这么搜出来 ！！
![各种TLE(超时)，不分析原因还会一直提交一直TLE](https://img-blog.csdnimg.cn/20200213152043549.png)
然而，当数据达到一定程度，我们使用简单的方法肯定会爆炸的，****。就可能需要一些特殊的巧妙方法处理，比如`各种剪枝`、`优先队列`、`A*`、`dfs套bfs`，又或者利用一些非常厉害的数学方法比如康托展开(逆展开)等等。而今天，我们谈谈**双向bfs**。
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200213152107792.png)

## bfs类问题
bfs又称广度优先搜索
- 估计大部分人**第一次**接触bfs的时候是在学习数据结构的**二叉树的层序遍历**！借助一个队列一层一层遍历。
- **第二次**估计就是在学习图论的时候，给你一个图，让你写出一个bfs遍历的顺序。

此后再无bfs...

而很多笔试面试还是其他机试其实对bfs的要求远远不止那么低的，需要能够处理一些小问题、写出对应代码。而事`bfs`可以处理很多问题，很多dfs搜索能够解决的问题bfs也能解决很多(相反也成立)，并且很多跟`状态`有些关系的用bfs更好控制，因为bfs借助的是一个**队列**实现，队列中储存节点就可以保存一些节点的状态。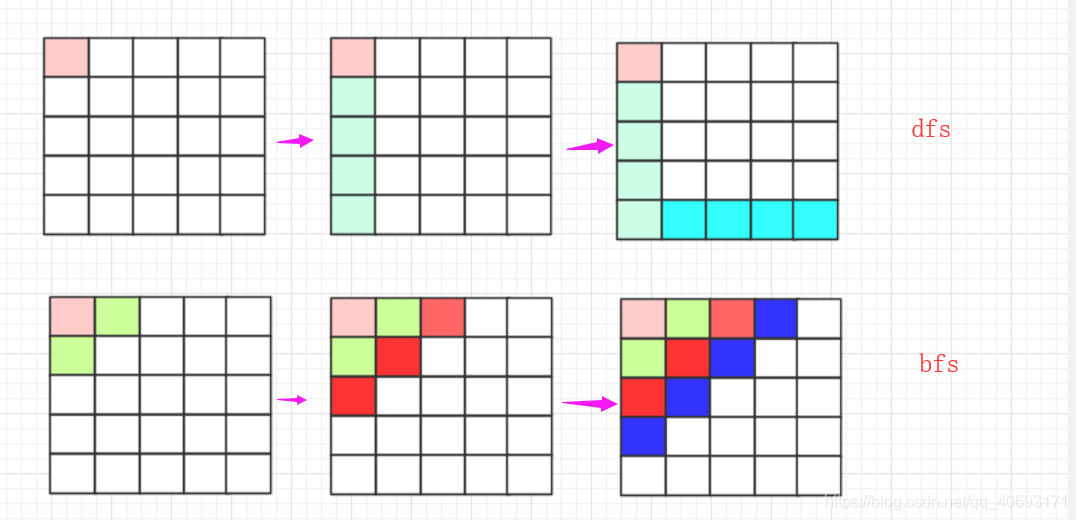
![](https://img-blog.csdnimg.cn/20190904001832921.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwNjkzMTcx,size_16,color_FFFFFF,t_70)
不过bfs并不是万能的，具体问题要看迷宫的大小的，迷宫长宽没增加一个数，那么这个数量级增加是非常大的，因为搜索次数大概和边长的指数级别有关系。当然这里不详细介绍bfs了，大家可以看以前的一篇文章。[数据结构与算法—图论之dfs、bfs(深度优先搜索、宽度优先搜索)](https://bigsai.blog.csdn.net/article/details/100185967)。

## 双向bfs
什么样的情况可以使用双向bfs来优化呢?其实双向bfs的主要思想是问题的拆分吧，**比如在一个迷宫中可以往下往右行走，问你有多少种方式从左上到右下。**
- 正常情况下，我们就是搜索遍历，如果迷宫边长为n，那么这个复杂度大概是2^n^级别.
- 但是实际上我们可以将迷宫拆分一下，比如根据对角线(比较多)，将迷宫一分为二。**其实你的结果肯定必然经过对角线的这些点对吧**！我们只要分别计算出各个对角线各个点的次数然后相加就可以了！
- **怎么算？** 就是从(0,0)到中间这个点`mid`的总次数为`n1`，然后这个mid到(n,n)点的总次数为`n2`，然后根据排列组合总次数就是`n1*n2`(n1和n2正常差不多大)这样就可以通过乘法减少加法的运算次数啦！
- 简单的说，**从数据次数来看**如果**直接搜索全图**经过下图的那个点的次数为`n1*n2`次，如果分成两个部分相乘那就是`n1+n2`次。两者差距如果n1,n2=1000左右，那么这么一次差距是平方(根号)级别的。从搜索图形来看其实这么一次搜索是本来一个`n*n大小`的搜索转变成n次(每次大概是`(n/2)*(n/2)`大小的迷宫搜索两次)。也就是如果18*18的迷宫如果使用直接搜索，那么大概`2^18`次方量级，而如果采用双向bfs，那么就是`2^9`这个量级。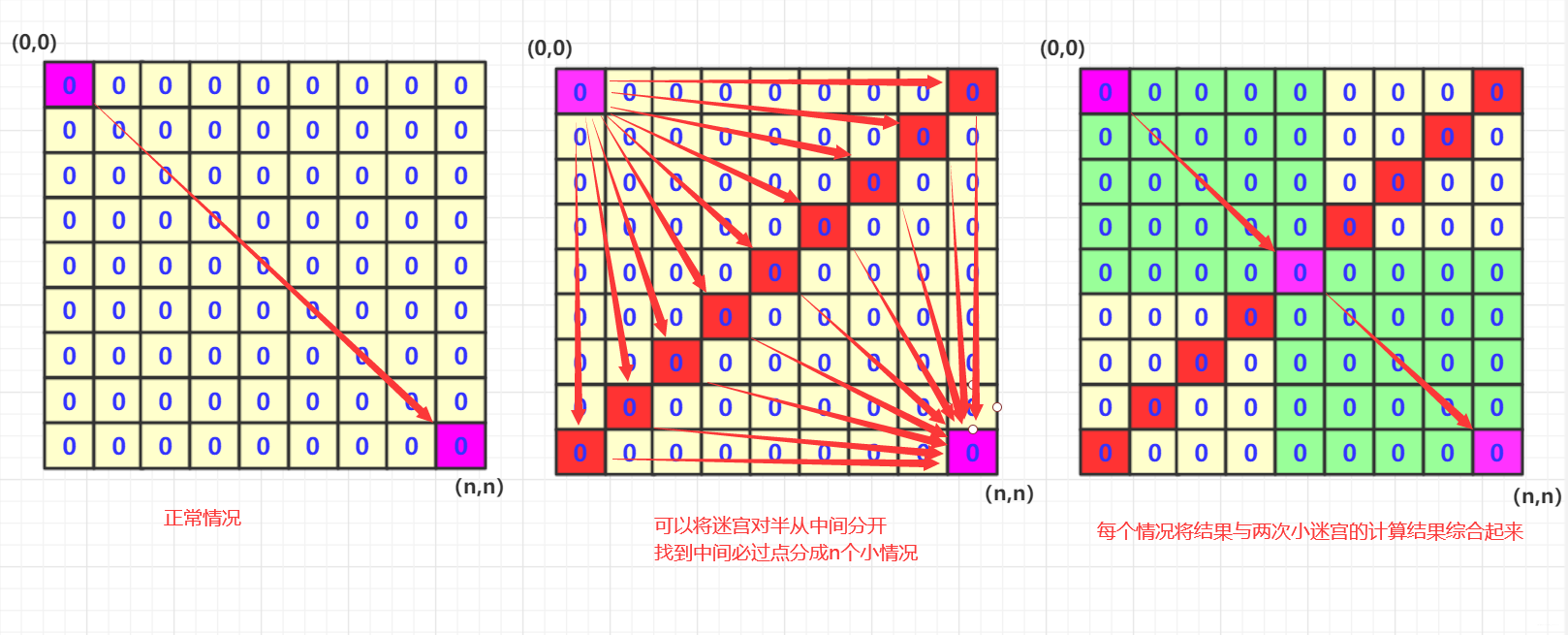

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200214160939877.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwNjkzMTcx,size_1,color_FFFFFF,t_70)

## 例题实战
题目链接：[http://oj.hzjingma.com/contest/problem?id=20&pid=8#problem-anchor](http://oj.hzjingma.com/contest/problem?id=20&pid=8#problem-anchor)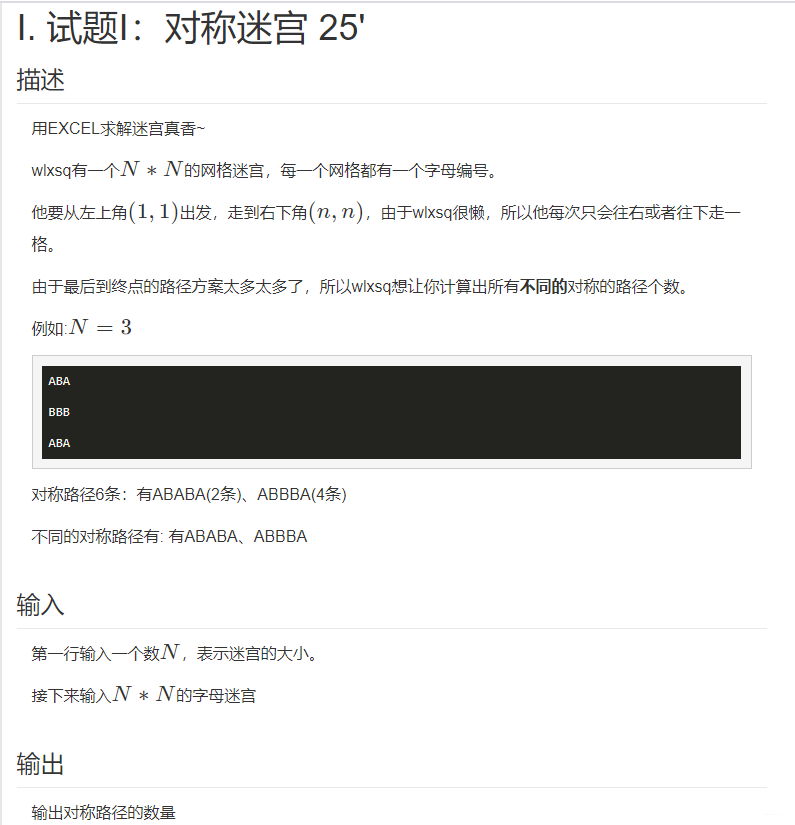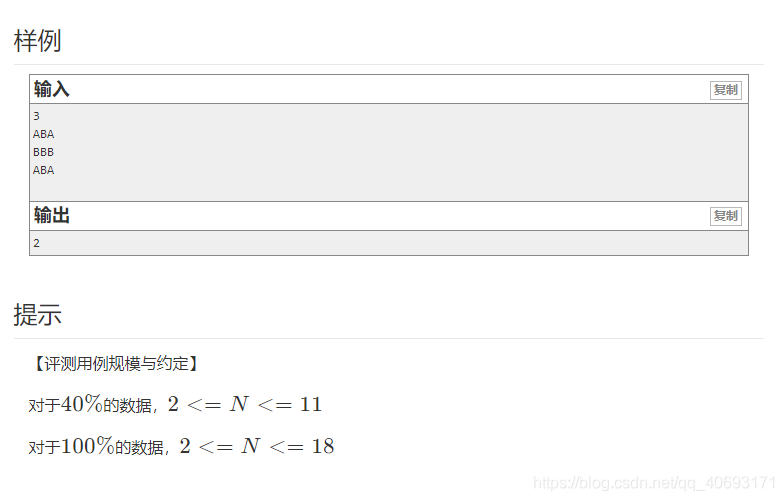

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200214224940741.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwNjkzMTcx,size_1,color_FFFFFF,t_70)

![在这里插入图片描述](https://img-blog.csdnimg.cn/2020021422551026.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQwNjkzMTcx,size_16,color_FFFFFF,t_70)
分析：对于题目的要求还是很容易理解的，就是找到所有的**路径种类**，再判断其中是**对称路径**的有几个输出即可！

对于一个普通思考是这样的，首先是进行dfs，然后动态维护一个字符串，每次跑到最后判断这个路径字符串是否满足对称要求，如果满足那么就添加到容器中进行判断。可惜很遗憾这样是超时的，仅能通过40%的样例。

接着用普通bfs进行尝试，维护一个node节点，每次走的时候路径储存起来其实这个效率跟dfs差不多依然超时。只能通过40%数据。

**接下来就开始双向bfs进行分析**！
- 既然只能右下，那么对角线的那个位置的肯定是中间的那个字符串的！**它的存在不影响是否对称的**(n*n的迷宫路径长度为`n-1 + n`为奇数).
- 我们判断路径是否对称，只需要判断从`(1,1)到对角节点k`(设为k节点)的路径**有没有和**从`(n,n)到k`相同的。**如果有路径相同的那么就说明这一对构成对称路径**
- **在具体实现上**，我们对**每个对角线节点**可以进行两次bfs(一次`左上到(1,1)`,一次`右下到(n,n)`).并且将路径放到两个hashset(set1,set2)中，跑完之后用遍历其中一个hashset中的路径，看看另一个set是否存在该路径，如果存在就说明这个是对称路径放到 **总的hashset(set) 中**。对角线每个位置都这样判断完最后只需要输出总的hashset(set)的集合大小即可！

ac代码如下：

```java
import java.util.ArrayDeque;
import java.util.HashSet;
import java.util.Queue;
import java.util.Scanner;
import java.util.Set;

public class test2 {	
	static class node{
		 int x;
		 int y;
		String path="";
		public node() {}
		public node(int x,int y,String team)
		{
			this.x=x;
			this.y=y;
			this.path=team;
		}
	}
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		Set<String>set=new HashSet<String>();//储存最终结果
		int n=Integer.parseInt(sc.nextLine());
		char map[][]=new char[n][n];
		for(int i=0;i<n;i++)
		{
			String string=sc.nextLine();
			map[i]=string.toCharArray();
		}
		Queue<node>q1=new ArrayDeque<node>();//左上的队列
		Queue<node>q2=new ArrayDeque<node>();//右下的队列
		for(int i=0;i<n;i++)
		{
			q1.clear();q2.clear();
			Set<String>set1=new HashSet<String>();//储存zuoshang
			Set<String>set2=new HashSet<String>();//储右下
			q1.add(new node(i,n-1-i,""+map[i][n-1-i]));
			q2.add(new node(i,n-1-i,""+map[i][n-1-i]));
			while(!q1.isEmpty()&&!q2.isEmpty())
			{
				node team=q1.poll();
				node team2=q2.poll();
				if(team.x==n-1&&team.y==n-1)//到终点，将路径储存
				{
					//System.out.println(team2.path);	
					set1.add(team.path);
					set2.add(team2.path);
				}
				else {
					if(team.x<n-1)//可以向下
					{
						q1.add(new node(team.x+1, team.y, team.path+map[team.x+1][team.y]));
					}
					if(team.y<n-1)//可以向右
					{
						q1.add(new node(team.x, team.y+1, team.path+map[team.x][team.y+1]));
					}
					if(team2.x>0)//上
					{
						q2.add(new node(team2.x-1, team2.y, team2.path+map[team2.x-1][team2.y]));
					}
					if(team2.y>0)//左
					{
						q2.add(new node(team2.x, team2.y-1, team2.path+map[team2.x][team2.y-1]));
					}
				}
				
			}
			for(String va:set1)
			{
				if(set2.contains(va))
				{
					set.add(va);
				}
			}
			
		}
		System.out.println(set.size());		
	}
}

```
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200214235616778.png)
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200214235721397.gif)