直线与三角形的重心坐标(Barycentric Coordinates)的推导与应用 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/361943207) 前言 -- 我们经常提到知道某个三角形三个顶点的属性,然后就可以求出三角形内部某一点对应的属性。例如深度缓存的时候,高洛德着色的时候等等,本文就来介绍一下这一部分内容。 想要计算三角形内部某一点对应的属性,也就是我们一直说的三角形的插值,就需要用到重心坐标的概念。 在讲三角形的重心坐标前,我们先来看一看直线上的重心坐标是怎么定义的。 求直线上任意一点 -------- 我们来看看怎么求直线上的任意一点,设我们有两个点 A  和 B  ,它们可以连成一条直线。那么该直线上的任意一点 P  必然满足: >  k 为一个常数,其值也很好求,取任意轴三个点值进行计算即可: >  然后我们可得: >  因为  即  而  通过向量的减法,我们可以理解为  ,同样的  ,那么就可得到  ,然后可以得到  ,最终简化可得: >  而  ,  ,  分别代表的就是 P,A,B 三个点的坐标,因此可得 > P = (1 - k)A + kB 因为 P = ((1-k)+k)P 因此上面式子可以变为 (1-k)A+kB-((1-k)+k)P=0 ,化简为 (1-k)(A-P)+k(B-P),即: >  直线上的重心坐标 -------- 通过上面的推导,我们就知道直线 AB 上的任意一点 P,都可以由一个 k 来计算出来的。当然了,也可以通过 P 来推出 k 的值,怎么求上面已经说明过了。 若我们设 j = 1 - k,那么 > P = jA + kB **这样的话我们 P 就可以使用 (j, k) 的方式来表示,这种表示方式就是我们的重心坐标。同时需要注意,因为重心坐标是根据某一条直线的 AB 两点所定义的,因此不同的直线各自会有各自的重心坐标。** 线性插值 ---- 通过前面直线的重心坐标我们可以得到,AB 两点内的任意一点满足:P = (1 - k)A + kB,我们将这个式子展开可以得到: > P = A + k(B - A) 一般情况下,我们 AB 两点是固定的,P 在 AB 之间移动,根据 P 的不同位置,我们可以算出 k 的值。这样我们就可以用这个特征来做 AB 之间其他属性的线性插值了。 例如假设 AB 两点同样代表两个颜色的值,求 AB 线段内任意一点 P 的颜色,只需要把 AB 的颜色值和通过 ABP 的位置求出来的 k 的值,带入上面的式子即可求出 P 的颜色值。 我们用 unity 简单的模拟下,代码如下: ``` public Image ImageA, ImageB, ImageP; float A_x, B_x, P_x, k; void Start() { A_x = ImageA.transform.position.x; B_x = ImageB.transform.position.x; } void Update() { P_x = ImageP.transform.position.x; //利用重心坐标,根据位置求出k k = (P_x - A_x) / (B_x - A_x); //用k计算出P的颜色,线性插值的方法 ImageP.color = ImageA.color + k * (ImageB.color - ImageA.color); } ``` 得到的效果为:  三角形上的重心坐标 --------- 与直线上任意一点满足 P = jA + kB 一样,在三角形 ABC 所在平面上的任意一点 P 同样满足 > P = iA + jB + kC > i + j + k = 1 **那么 P 用 (i, j, k) 的方式表示,就是在三角形上的重心坐标。**同样的,因为重心坐标是由三角形的三个顶点所定义的,因此不同的三角形有各自的重心坐标。 同样的,**若点 P 要在三角形内部或边上,需要满足 i >= 0,j >= 0,k >= 0**,否则点 P 在三角形所在平面外。 同样由于 P = (i+j+k)P = iP+jP+kP,因此我们可得到 iA+jB+kC-iP-jP-kP = 0 即: >  三角形和直线的关系 --------- 我们将三角形 ABC 的某个顶点(例如 C)和三角形内任意一点 P 连线,并衍生到三角形的某条边上,设交点为 D,如下图:  那么 D 点在 AB 上的位置,我们不就可以用直线的重心坐标表示么,我们设:D = xA + yB,其中 x + y = 1 知道 D 点坐标后,那么 P 点在 CD 的坐标我们又可以用直线的重心坐标表示,我们设:P = wC + zD,其中 w + z = 1 把 D 带入得:P = wC + z(xA + yB) = zxA + zyB + wC,而 zx + zy + w = z(x + y) + w = z + w = 1 那么设 i = zx,j = zy,k = w,不就证明了 P = iA + jB + kC 成立。 解 i,j,k 的值 ---------- 接下来,我们来看看 i,j,k 三个值怎么计算,因为 i+j+k=1,因此 k=1-i-j,也就是只要求两个未知数 i 和 j 即可。那么我们只需要找到两个方程组,解二元一次方程式即可。 因为 P = iA + jB + kC,因此  从中我们就可以取得两个方程式:  注:取 x,y 的话,也方便在二维空间中理解,当然也可以去 x,z 或 y,z 去计算。 解得  去 i ,得  此时方程式中只有一个 j 是变量,我们继续解,得  解得  解得  去分母,解得  即可求得 j 的值: >  同理可解的 i 的值: >  至于 k 的值,1-i-j 即可。 三角形重心坐标的几何意义 ------------ 我们将点 P 和三个顶点分别连线,可以得到三个新的三角形,如下图:  我们设三角形的总面积为 s,三角形 PBC 的面积为 a,三角形 PAB 的面积为 c,三角形 PCA 的面积为 b,那么可得: >  >  >  也就是说重心坐标和每个顶点所相对的三角形(例如 A 对应的是 PBC)的面积比有关。 我们来简单的推导一下: 前面我们知道  而  的值,不就是  的 x 值么,我们标记为  ,其他项也同理,那么我们可以得到  不知道大家对上面的这种  式子熟不熟悉,它正是二维向量叉乘的模(不熟悉的可以看下[叉乘相关知识](https://blog.csdn.net/wangjiangrong/article/details/107770259))。因此我们可以得到 >  设夹角 CBP 为 α ,那么分子  正是三角形 CBP 的面积 同理分母就是三角形 ABC 的面积,因此  成立,其他也同理。 实际应用场景 ------ 前面哔哔赖赖了一大堆,我们知道可以通过重心坐标来计算三角形内某点的坐标,即 > P = iA + jB + kC ABCP 代表的都是位置信息,我们可以通过位置信息求出重心坐标。而重心坐标牛逼就牛逼在,我们可以把 ABCD 的信息用别的任何信息来代替,例如颜色,法线,uv,深度等,然后套用上面的公式即可求出 P 点对应的属性。 例如我们 A 点红色 (1,0,0),B 点绿色 (0,1,0),C 点蓝色 (0,0,1),那么三角形内任何点的颜色就等于它的重心坐标,例如重心点颜色为  我们可以简单的用 Unity 写个 demo 验证一下 首先用下面脚本绘制一个三角形,三角形内部的颜色 Unity 已经为我们插值好了 ``` [ExecuteInEditMode] public class Triangle : Graphic { Vector2 positionA = new Vector2(70, 40); Vector2 positionB = new Vector2(100, 100); Vector2 positionC = new Vector2(40, 70); protected override void OnPopulateMesh(VertexHelper vh) { vh.Clear(); vh.AddVert(positionA, Color.red, Vector2.zero); vh.AddVert(positionB, Color.green, Vector2.zero); vh.AddVert(positionC, Color.blue, Vector2.zero); vh.AddTriangle(0, 1, 2); } } ``` 效果如下(注意 color space 要使用 gamma 的):  然后怎么验证呢,我们可以创个小 Image,然后通过它的坐标和三个顶点的坐标,我们就可以计算出小 Image 所在点对应的重心坐标,知道重心坐标和三个顶点颜色后,就可以计算出对应颜色,赋值给小 Image,然后对比下颜色即可。代码如下: ``` using UnityEngine; using UnityEngine.UI; public class NewBehaviourScript : MonoBehaviour { public Image self; Vector2 a = new Vector2(70, 40);//red Vector2 b = new Vector2(100, 100);//green Vector2 c = new Vector2(40, 70);//blue void Update() { Vector2 p = transform.position; float i = (-(p.x - b.x) * (c.y - b.y) + (p.y - b.y)*(c.x - b.x)) / (-(a.x - b.x)*(c.y - b.y) + (a.y - b.y)*(c.x - b.x)); float j = (-(p.x - c.x) * (a.y - c.y) + (p.y - c.y)*(a.x - c.x)) / (-(b.x - c.x)*(a.y - c.y) + (b.y - c.y)*(a.x - c.x)); float k = 1 - i - j; Debug.Log($"({i}, {j}, {k})"); self.color = new Color(i, j, k); } } ``` 效果如下: 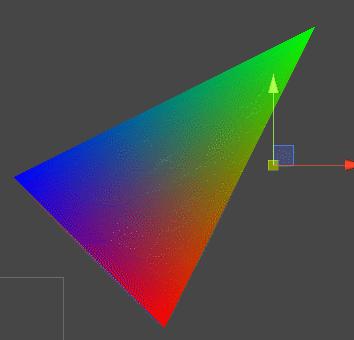 可以看出在三角形内部时,我们计算得到的颜色和 Unity 做好的插值是一样的。 至于除了颜色外的其他属性插值,原理也都是一样的,只要了解重心坐标了即可。也就是说**我们只需要先通过四个点的位置信息算出重心坐标,然后就可以通过重心坐标来计算其他属性的插值**。 重心坐标与投影 ------- 前面一套套下来,我们可能会有个疑惑,重心坐标的计算和 z 轴没有关系么? 注:其实更准确的说法是只和 x,y,z 中其中任意两项有关,具体可以看求 i,j,k 时,我们取的二元一次方程式是哪两个轴,当然通常情况下,就是取的 x 和 y。 不考虑 z,等于把空间中的三角形去掉 z,即投影到平面 xy 上,即原本的 A 点  ,B 点  ,C 点  变成了 A'点  ,B'点  ,C'点  。原本空间中三角形内的 P 点  ,同样投影变成了 P' 点  。那么投影前后,P 和 P' 的重心坐标一样么?答案是一样的! 公式没考虑 z 其实就已经告诉我们答案了,那么几何上,我们怎么理解呢,我们可以看个最简单的例子,就是重心。 我们假设下图中的三角形是空间中的三角形,也就是 ABC 的 z 轴值不同,重心点 O 的重心坐标自然是  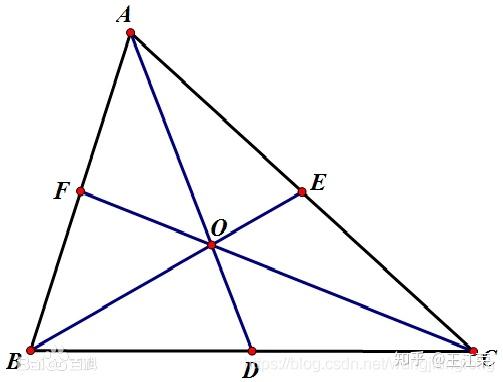 那么我们看看投影后还是不是  就可以了。 很简单,我们先来看边 BC 的投影,如下图,我们在 yz 平面看边 BC 的投影  可以发现投影后 D'依旧是 B' 和 C'的中心点(相似三角形原理),也就是说投影后的直线 A'D'是三角形 A'B'C'的中线。其他中线同理,因此投影后 O'的还是三角形 A'B'C'的重心,其重心坐标还是  。 但是!有一种投影不行,就是透视投影,依旧是上面的三角形的边 BC,我们来看看透视投影会发生什么,如下图: 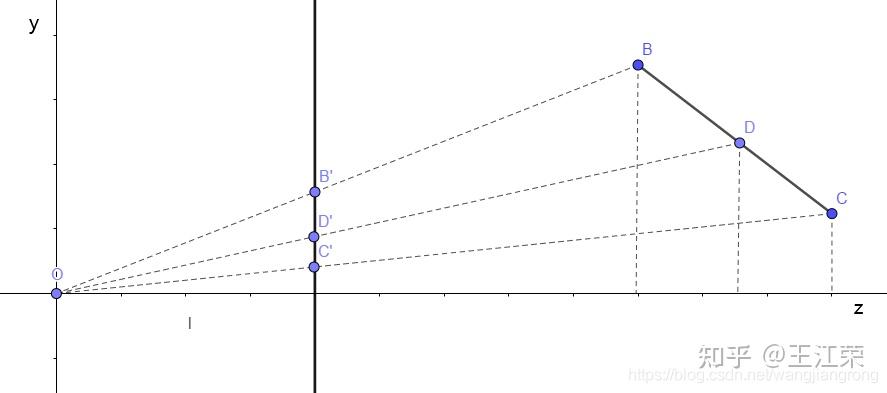 很明显我们就可以看出来,此时 D'不再是 B' 和 C' 的中心点。当然了,数学不能光用眼睛看,我们需要推导 为了方便计算,我们设 O 点为原点,O 到投影屏幕的距离为 l (如上图所示),根据相似三角形可以得到:  ,即:  。同理可得  ,  由于 D 是 BC 的中心点,根据直线的重心坐标我们可以知道  ,  ,带入可得:  ,而投影后 B'C'的中点的 y 值应该是  ,可以发现和  并不相等。但是有个前提,那就是  ,否则  ,上面的式子依旧相等。 用图来看的话更直观,如下图(依旧是相似三角形): 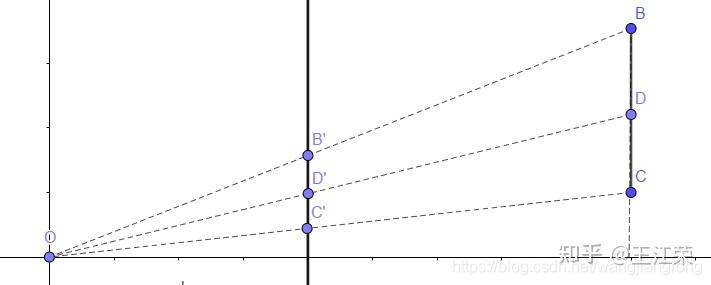 而三角形重心坐标的这个变化同样适用于直线的重心坐标,事实上我们的举例就等于在看直线的重心坐标变化。 因此可以得出结论,**在空间中的三角形或直线内的某个点,在投影变换前后,其的重心坐标可能会发生改变。因此有些计算,例如深度,一定要在投影变换前做,否则得到的结果可能是不对的**。 矫正 -- 但是前面那样太麻烦了,我们可不可以直接在知道变换前的重心坐标推出变换后的重心坐标,或者反过来呢?当然可以。 我们先从直线的重心坐标投影矫正开始,直接使用之前的图,如下: 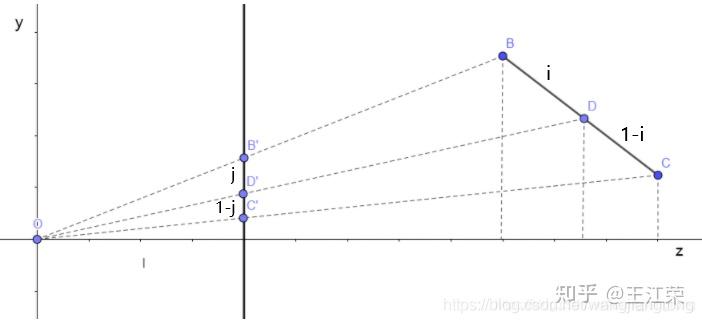 此时 D 不再是 BC 的中心点了,而是当做 BC 中的任意一点。根据直线的重心坐标我们可以设: D = iB+(1-i)C,D 的重心坐标即为 (i, 1-i)。直线 BC 通过透视投影后得到直线 B'C',点 D 变为 D',我们知道透视投影后,重心坐标的值会变,所以我们设:D' = jB'+(1-j)C',D'的重心坐标即为 (j, 1-j)。 那么我们只需要知道 i 和 j 的相对关系,不就可以在只知道 i 或 j 中一个的情况下推出另个的值了么?例如,我们假设 i = 2j,那么投影前的重心坐标 (0.6, 0.4) 在投影后自然变成的了 (0.3, 0.7),或者说投影后的重心坐标为 (0.1, 0.9),那么投影前就是 (0.2, 0.8)。这样即使碰见投影变换,我们也可以通过变换后的重心坐标去推导出原本的重心坐标,不用再通过**逆变换**去求原本的重心坐标了。 当然前面 i = 2j 是我们瞎鸡儿说的,我们来看看真正的值是多少。 根据直线的重心坐标,我们可以很容易求得 j 的值:  (其实 i 的值同样可以直接算出来,然后和 j 一除就知道了,但是我们这边要推导出一个更简单的公式)。 通过相似三角形可以得到:  ,  ,  ,带入 j 中可得:  。 我们先来看分子项,即  ,我们知道  ,  ,带入分子中,得到:  化简可得:  其中的  不就是分母中的那部分嘛,即可抵消掉,j 就可以简化为: >  从这个式子也可以看出,z 值相同时,则 i = j,重心坐标不变。也说明了之前一大串的  的值其实就是 i 。 做了个简单的验证,如下图,D 点的重心坐标确实正好从 (1/3, 2/3) 变成了 (1/6, 5/6)。 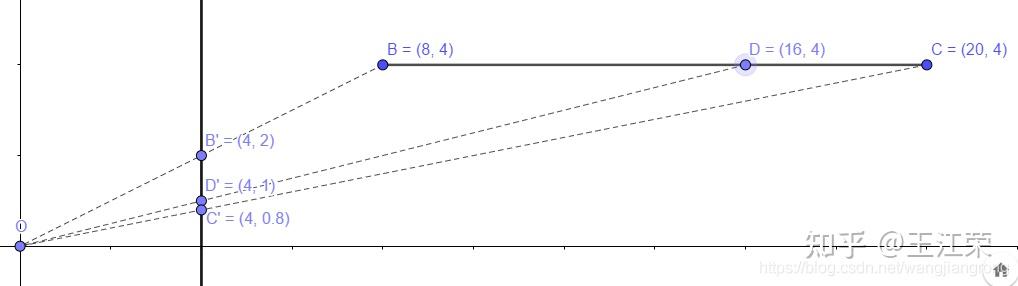 接下来我们来讲讲三角形的重心坐标投影矫正 前面我们得到  ,那么三角形内任意一点 P,我们可以看作是 AD 上的任意一点,我们设 P = wA+(1-w)D,投影后 w 会变为 z,套用上面的公式,我们可以得到 >  因为 P = wA+(1-w)D,D = iB+(1-i)C,所以 P = wA+(1-w)(iB+(1-i)C),即: > P = wA+(i-iw)B+(1-i-w+iw)C 也就是 P 的重心坐标为 (w, i-iw, 1-i-w+iw) 后面两项看着很复杂,我们先不管,写成 (w, ?, ?),那么我们就知道投影后重心坐标会变为  。 那后面两个怎么算呢?既然我们可以把 D 看成是 BC 上的一点,P 是 AD 上的点,那么是不是可以再把 D 看成 AB 或 AC 上一点,P 则是 CD 或 BD 上一点来推导上面的公式。 这样我们又会得到  和  **因此得出结论,假设在透视投影前,P 在三角形 ABC 的重心坐标为 (i, j, k),那么投影后该坐标会变为**  **,而**  使用Raymarching和DistanceFunction绘制3D几何 向量运算与应用