着色与Blinn-Phong反射模型 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/364086530) 什么是着色(Shading) -------------- 在[光栅化](https://zhuanlan.zhihu.com/p/363245957)过程中,我们可以通过像素与三角形的对应关系,然后为像素填充三角形对应的颜色,也就是物体本身的颜色(这个颜色一般来源于模型对应的 material 里设置的一个颜色值)。此时我们要渲染一个黄色的立方体的话,会得到如下的效果:  咋一看好像没啥问题,利用上空间想象力,它确实是黄色的立方体,但是为什么这么不直观呢?这是因为前面的操作中我们并没有考虑光照等信息对物体表面的表现力的影响,更加真实一点的着色结果应该如下:  从该图我们可以看出,虽然它还是一个黄色的立方体,但是在不用的面上有明有暗,也就是说实际上每个像素的颜色其实都是有色差的。这些明暗效果给了我们更真实的感觉。 再来看个更加复杂的例子,如下图:  同样的,图中的瓷器表面显示的有明有暗,其中甚至还有反射出来的倒影。而且我们一眼能看出图中的杯子是陶瓷杯子而不是金属杯子,塑料杯子,这也是因为着色结果给我们的材质感。 因此着色不仅仅只考虑物体本身的颜色,还要考虑物体的材质,环境的光照等等。 在图形学中,我们可以把**着色定义为在不同物体上应用不同材质的过程**。因为不同材质和光产生的相互作用就会不同,例如反射率,折射等。和光的不同作用就会显示出不同的结果,因为我们能看见物体都是因为光线进入了人眼。 那么接下来自然是要看看怎么进行着色,这里我们要介绍 **Blinn-Phong 反射模型**,但是在这之前我们先来看一些与着色有关的知识点。 着色点(Shading Point) ------------------ 对于整个物体受到光照的结果,我们依旧进行细分,将其理解成物体表面每一块极小区域受到光照的结果,这一小块区域我们称之为着色点。因为是极小一块区域,因此即使物体表面是曲面,我们也可以把一个着色点当作是一个平面,如下图:  根据每个着色点,我们可以有如下一些定义: 1. 既然是平面,那么我们就可以定义其对应的法线,即图中的 n 向量。 2. 光源对应着色点的方向,即图中的 l 向量,可通过光源位置减去着色点位置然后归一化得到,若多个光源,则每个光源有一个对应的方向。 3. 摄像机 / 人眼对应着色点的方向,即图中的 v 向量,可通过摄像机位置减去着色点位置然后归一化得到。 4. 表面的一些属性,例如颜色(color),亮度(shininess)等等。 注:上面提到的三个向量代表的都是方向,因此它们都为**单位向量**。 同时我们在考虑着色时,**不需要考虑阴影**,即不用考虑某个着色点的光照被其他物体遮挡的问题。我们只考虑该着色点本身的各个属性即可,这也是着色的局部性,因此**着色过程中也不会产生阴影**。 光与颜色 ---- 通过物理的学习,我们知道**可见光是由不同颜色的光波**所组成的,物体之所以有颜色是因为对光线不同程度的吸收所导致的。 例如物体把所有光线都吸收了,那么它就是黑色,反之如果都不吸收,那么就是白色,而红色就是吸收了除了红色以为所有的光。 因此我们可以假设着色点有一个属性,我们可以通过调整这个属性来达到显示不同的颜色,即吸收或反射哪些光。 Lambert's 余弦定率 -------------- 光是有能量的,同时物体也会吸收这些能量,例如光照下东西会变热,四季变换也是这个原理。 那么我们来看下不同方向的光照对于着色点(着色点面积大小固定)的影响,如下图: 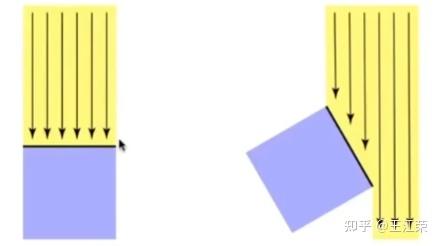 假设我们把一束光离散成几根光线,那么可以发现当我们的着色点和光照方向形成不同的夹角时,所接受到的光线数量也有所不同。因此着色点在不同角度下得到的光照能量不同,所以着色点所显示的亮度也应该有所不同。  如上图,光照方向我们前面定义了为 l 向量,着色点方向即可以理解为法线方向 n 向量,因此它俩的夹角 θ (cosθ等于 l 和 n 向量的点乘)即可决定该着色点可以接收到多少的光照能量。 上诉所说的就是 **Lambert 的余弦定率**:平行光线对某吸收面上的强度,与其入射角的余弦成比例。 能量传播 ---- 前面提到了光的能量,那么这个能量哪来的呢?肯定是光源所产生的。我们假设有一个点光源,它每时每刻会往均匀的往所有方向发射光。因为在同一个介质中,光速是相同的,因此假设在 t0 时刻点光源发射了光,那么在 t1 时刻,这些光的能量肯定都均匀的分布在一个球面上,如下图,展示的二维的情况: 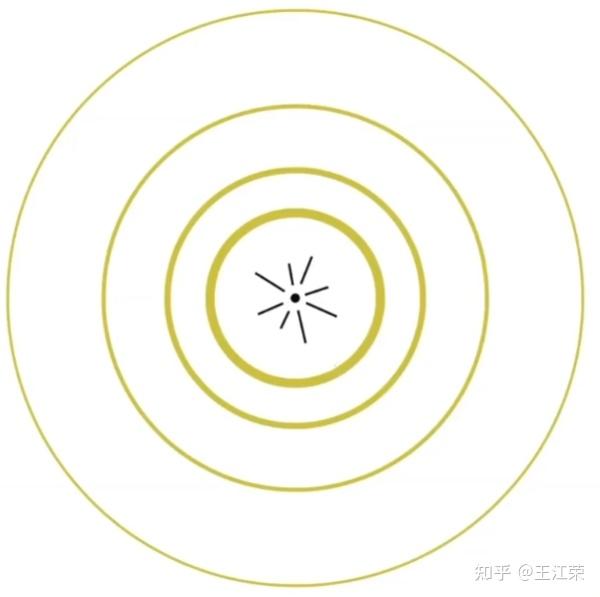 因为能量守恒的原理,我们假设在传播过程中能量不损失,那么某一时刻的光在传播时,它所围成的球面会越来越大,但是总的能量依旧不变,因此球面上一个固定面积的能量随着传播是越来越少的。 球的面积公式为  ,我们假设球半径为 1 时,单位面积上的能量为 I 。那么当球半径为 r 时,此时单位面积上的能量即为  ,即**成半径平方的反比进行衰减**。 着色点接收到的光的能量 ----------- 通过前面的介绍,我们就可以很轻松的计算出一个着色点接收到的光的能量。  如图,接着我们定义着色点到光源的距离为 r,光源在半径为 1 时对着色点的能量为 I,那么该着色点能接收到的能量 L 为: >  为什么要  呢?因为如果光源在着色点的背面,即 θ > 90° 的情况下,此时点乘为负数,我们就当做没有光照,取 0 。 Blinn-Phong 反射模型(Reflectance Model) ----------------------------------- 我们先来看下面这张图,分析一下图中的模型与光照的作用情况。  首先从图中我们可以看出光照应该是从右上方照射过来的,因为左边偏暗右边偏亮。我们可以在杯子的右边看见有一部分亮的发白,通过物理学我们知道,越亮说明进入人眼的光线越多,因此对于这一部分我们可以当成是发生了镜面反射,把光线全部反射到了我们的人眼或者摄像机中,我们称这一部分为**高光(Specular highlights)**。 然后杯子正对着我们的部分就不如高光部分那么亮了,这一部分我们称之为**漫反射(Diffuse reflection)**,因为漫反射会把光线反射到四面八方去,不如镜面反射那么集中,所以会暗一些。 最后我们来看看杯子左边的部分,前面我们知道光源在杯子右边,那么理论上杯子左边就不会被光源所直接照射到,没被光源照射到不应该是黑色嘛,可是图中在这部分虽然更暗了点,但还是显示了杯子的颜色,这是为什么呢? 因为我们的光线打到物体后会发生反射,而反射后的光依旧还可以打到其他物体再发生反射,多次反射后后,最后到我们的人眼当中,对于这些反射后的光,我们称之为**间接光照**。例如图中光线打到桌面,瓷盘或者墙上,发生了漫反射,漫反射后的间接光就可能会打到杯子的左边部分,然后在由杯子左边部分漫反射到我们人眼当中,从而照亮了杯子的左边部分。 但是由于间接光照比较复杂(光线追踪中会使用到),这里我们假设杯子左边会接收到来自四面八方的反射光,并把它们简化成是一个常量,这部分即为**环境光(Ambient lighting)**。 那么也就是说我们只要模拟好上面所说的高光,漫反射和反射光三项,就可以实现出和图中一模一样的效果来了,这种模拟方式我们就称为 Blinn-Phong 模型。 Blinn-Phong 模型是一种简单的着色模型,此外还有 Phong 模型,Lambert 模型等,区别就在于对光的作用的不同理解和计算。同时**这些模型并不是真正的完全都按照物理方法来计算的,很多计算方式都进行了理想化 / 简化**,因此前面描述的时候,就说了很多的假设。不过得到的效果还是相对比较真实的,就是上面的图片一样。 现在图形 API 推出了[基于物理的渲染 (Physically Based Rendering,简称 PBR)](https://learnopengl-cn.github.io/07%20PBR/01%20Theory/),它指的是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合。这种渲染方式比 Phong 或者 Blinn-Phong 光照算法总体上看起来要更真实一些。 接着我们来看看怎么模拟 / 计算 Blinn-Phong 模型的高光,漫反射和反射光三项。 漫反射(Diffuse Reflection) ----------------------- 何为漫反射?即光线从一个方向照射到一个物体后,会被**均匀**的反射到各个方向去。 在前面我们已经知道了一个着色点能接收到多少能量 L 了,结合前面提到的颜色原理,我们只需要定义一个系数  ,即可决定该着色点最终的结果,公式如下: >  例如 kd=1 即反射所有的光,那么就是白色, kd=0, Ld 就等于 0,即不反射任何光,即为黑色。 注,因为要表示的是颜色,因此实际上 kd 和 Ld 并不是一个 0 到 1 的实数,而是一个三维的数,例如 (0,0,0)。 通过不同的 kd 值,我们就可以定义出着色点不同的颜色。如下图,光源在左上角,随着 kd 的变大,被光照射的部分也越来越亮。同时可以发现相同 kd 的情况下,球的左上角亮于中间部分,这也是 Lambert 的余弦定率的结果,因为法线和光照的夹角大,接收到的能量小,所以暗。  因为漫反射是将均匀的反射出去,所有我们不管在任何方向看,结果都应该是一样的,因此式子也和观察方向 v,没有什么关系。 注:在 Blinn-Phong 模型中,我们不会考虑摄像机和着色点的距离而产生的能量损失。也就是说不会有因为观察距离远,而导致物体看着变暗的效果。 高光(Specular Highlighting) ------------------------- 高光是类似于镜面反射的结果造成的,我们知道镜面反射时,出射角和入射角的角度相同的。如下图,所有的入射光都会被反射到 R 方向附近上去,因此只有当我们的摄像机方向 v 和 R 离得很近时,我们才能看到反射光,因为光线很集中所以形成了高光效果。  那么我们势必要求出 R 的值来,才能知道 R 和 v 是否接近,然而这个 R 虽然能求,但是其实并不好求,有不少的计算量。Blinn-Phong 模型在这里做了很聪明的一步,它发现我们只需要求出 l 和 v 的半程向量 h(即:l 和 h 的夹角等于 v 和 h 的夹角),然后把它和法线 n 作比较即可,如下图:  我们可以很容易的看出,如果 v 正好在出射方向上,那么 n 和 h 重叠,否则 v 离出射方向越远,n 和 h 也会越远。 而 h 相比之前的 R 就好求的太多了,通过向量加法的平行四边形法则我们知道,v+l 可以看作是形成了一个平行四边形,其对角线即为加法后的结果。又因为 v 和 l 都是单位向量,因此这个平行四边形就是**菱形**,其对角线就是分割线,也就是半程向量 h 的方向,然后我们做个归一化即可: >  这里也是 Blinn-Phong 模型和 Phong 模型的一个区别,在 Phong 模型中,我们需要求出 R 的值,而在 Blinn-Phong 模型中,我们只需要求 h 的值即可。 然后要判断 h 和 n 是否接近,我们只需要知道它们的夹角即可,也就是说把 h 和 n 相点乘即可。因此我们可得到如下公式: >  ks 和漫反射的 kd 类似,属于一个我们定义的系数,通常情况下高光是白色的,因此 ks 的值也为白色相对应的值。 我们可以发现在高光的公式中,并没有考虑 Lambert's 余弦定率(即没有  项),在这里它被 Blinn-Phong 模型给简化掉了,主要关注的是是否能看见高光。 此外在高光的公式中还多了一个指数 p,等于**对夹角的余弦值做了个幂运算**,为什么要这步操作呢?我们先来看看对余弦做幂运算会有什么结果,如下图: 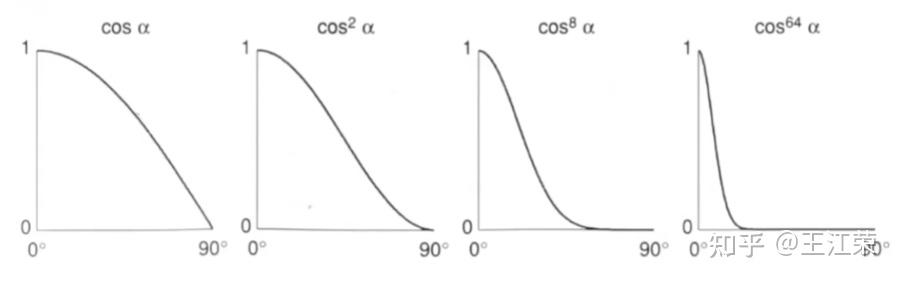 如果没有 p 指数或者 p=1,我们会发现假如夹角 45 度,  的值约等于 0.7,也就是说依旧能看见很明显的亮度,但是我们不希望这种情况出现,因为 45 度左右我们就不应该能看见高光了。因此我们增加了指数 p,从图中可以看出,当 P 的值越大,  的值就越快接近于 0,这样就不会造成当夹角较大时,我们依旧能看见高光的现象了。通常情况下,在 Blinn-Phong 模型中 p 的取值会是在 100-200 之间。 我们来看看实际效果,如下图:  图中是漫反射 + 高光的效果,小球整体效果就是漫反射的结果,而其中较小的那些小圈就是加上高光后的结果。可以看出 ks 越大,小圈越亮,因为反射的光越多。p 越大,小圈越小,因为偏移一点角度就会使 cos 的值为 0。 环境光(Ambient lighting) --------------------- 因为光线可以不断的折射,因此即使没有被光源直接照射到的着色点依旧可能被间接光所照射到,从而产生亮度。但是这一部分的计算非常的复杂,因此在 Blinn-Phong 模型中,我们假设每个着色点接收到的环境的光永远都是相同的,假设为  。  如图,因为是环境光,因此和光源方向 l 以及着色点法线 n 就没有关系,同样的应该不管从什么方向看,结果都应该是一样的,因此和视线 v 也没有关系。 因此我们就可以得到环境光的公式 >  与其他公式类似,也会有个系数 ka ,用来控制能反射多少能量。因此环境光就是一个常量,可以当作代表的就是某一种颜色,也就是说物体上的每个着色点都带有这个颜色,因此整体效果也会比较平滑。 三者相加 ---- 前面我们分别介绍了着色点上三者不同类型的光照效果,那么我们只需要把三者相加即可得到我们的最终效果,公式如下: >  效果图如下:  使用上诉方法进行着色,就是我们所说的 Blinn-Phong 着色模型。当然了,很多都是假设得到的结果,因此 Blinn-Phong 着色模型得到的结果只是一个近似真实环境的结果。 自己也简单利用 shadertoy 模拟了一下,有兴趣可看: [王江荣:Shadertoy 模拟 Blinn-Phong 模型着色效果](https://zhuanlan.zhihu.com/p/367712078) 着色频率(Shading Frequencies) ------------------------- 既然我们前面提到了着色是给每个着色点进行着色,而着色的方法 / 公式上面已经介绍了其中一种了,那么在实际的着色过程中,着色点到底是什么? 我们先来看看下面这张图:  上图中的三个球,从边缘我们可以发现它们属于相同的几何模型,但是我们可以看出着色出来的结果却是各不相同。 * 第一个球,我们可以明显看出它是对 Mesh 的每个面进行着色,也就是说我们的着色点实则是一个个的面。 * 第二个球,则是把每个面的顶点当做着色点进行着色,那么一个面的不同顶点就可能是不同的颜色,面内某一点的颜色可以使用插值的方法来计算。 * 第三个球,自然就是把每个像素当做一个着色点进行着色。 这些着色方法的不同,我们称之为着色频率不同,可以看出不同的着色频率会产生不同的效果。 平面着色(Flat Shading) ------------------ 平面着色就是对每个三角形面进行着色(shade each triangle),因此每个三角形内部的颜色都会是一样的,效果如下:  关于着色的计算,三角形的法线很好求得,将两条边进行叉乘即可。光源方向与距离和摄像机方向自然也是根据每个三角形而计算。 相对而言,这种方法得到的效果并不算特别好。 高洛德着色(Gouraud Shading) ---------------------- 高洛德着色,又称平滑着色(Smooth Shading),它则是针对顶点的着色(shade each vertex),效果如下:  我们只要求出每个顶点的法线,即可计算出每个顶点的着色,那么顶点的法线应该怎么计算呢?我们知道一个顶点可能连接着多个不同的三角形面(如下图),而每个三角形面都会有它各自对应的法线,那么这个顶点的法线值就是这些面的法线值的平均。  公式如下: >  注:更准确的算法是,根据每个三角形的面积求一个权重,面积越大权重越高,然后根据权重来计算顶点的法线。 知道每个三角形的顶点颜色后,三角形内部某个点的颜色根据重心坐标方法即可计算。 可以看出效果比之前的平面着色好了很多。 有关重心坐标的介绍,可以看之前的文章 [王江荣:重心坐标(Barycentric Coordinates)](https://zhuanlan.zhihu.com/p/361943207) 冯氏着色(Phong Shading) ------------------- 冯氏着色则是针对每个像素的着色(Shade each pixel),效果如下:  与之前提到的 Blinn-Phong 着色模型一样,都是由 Phong 发明的。 既然每个像素着色,那么自然要计算每个像素的法线,我们知道每个像素会对应到一个三角形的平面,但是它们的法线并不是平面的法线,而是根据三个顶点的法线来进行插值计算,如下图: 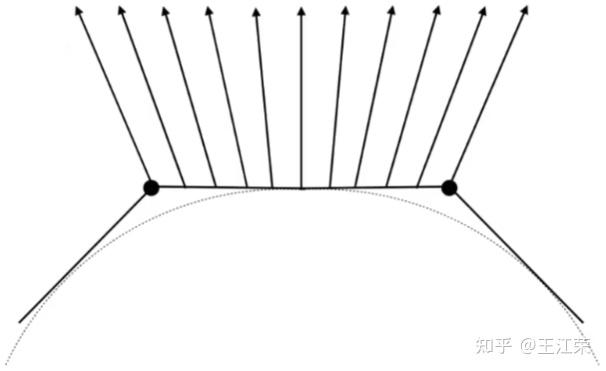 中间的这些即是像素的法线,根据两个顶点的法线通过重心坐标的方法计算得到。 可以看出,这种方法得到的着色效果就非常的好了。 三者的对比 ----- 三种着色的效果对比如下: 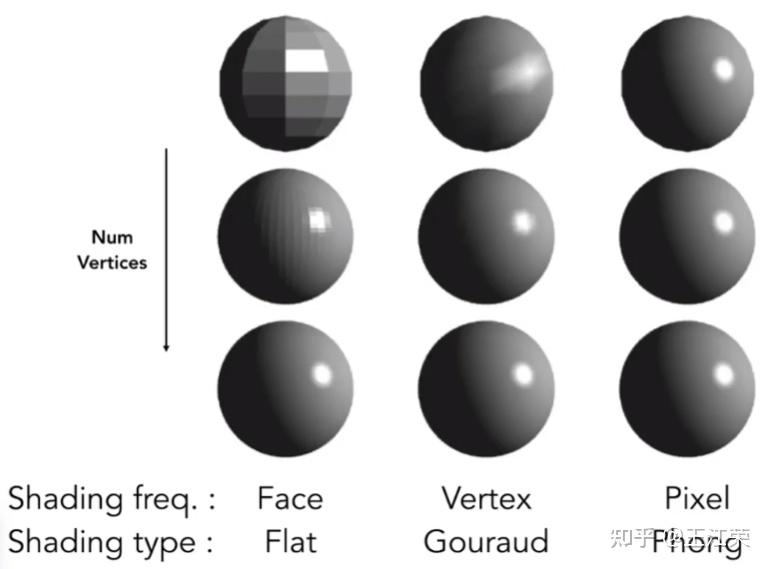 可以看出,当模型面较少时,平面着色的效果最差,冯氏着色的效果最好。但是当模型的面越来越多时,三者的效果也基本相似。 光栅化过程中的采样与反走样(MSAA),频域与滤波 【Unity笔记】ShaderLab与其底层原理浅谈