算法 agile Posted on Jun 18 2023 算法 ### 判断矩阵相交 首先求出P1与P3点在X方向较大值与Y方向较大值的交点,在下图中就是P3,用红点(记为M点)表示。然后求出P2与P4点在X方向较小值与Y方向较小值的交点,在下图中就是P2,用橙色点(记为N点)表示。如果M点的X坐标和Y坐标值均比N点相应的X坐标和Y坐标值小,亦即M和N可以分别构成一个矩形的左上角点和右上角点,则两矩形相交;其余情况则不相交。 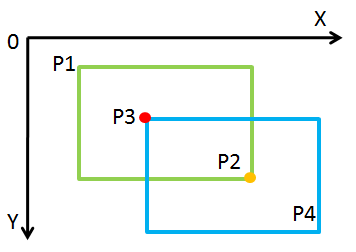 ``` C++ class Solution { public: int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) { int s1 = (C - A) * (D - B), s2 = (G - E) * (H - F); int mix = max(A, E), miy = max(B, F), maxx = min(C, G), maxy = min(D, H); if(mix <= maxx && miy <= maxy){ int s3 = (maxx - mix) * (maxy - miy); return s1 + s2 - s3; } else return s1 + s2; } }; ``` ### 快速排序 ``` C# using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace QuickSort //***对相同元素, 不稳定的排序算法*** { //相对来说,快速排序数值越大速度越快 。 快速排序是所有排序里面最快的 class Program { static void Main(string[] args) { int[] arr = { 15, 22, 35, 9, 16, 33, 15, 23, 68, 1, 33, 25, 14 }; //待排序数组 QuickSort(arr, 0, arr.Length - 1); //调用快速排序函数。传值(要排序数组,基准值位置,数组长度) //控制台遍历输出 Console.WriteLine("排序后的数列:"); foreach (int item in arr) Console.WriteLine(item); } private static void QuickSort(int[] arr, int begin, int end) { if (begin >= end) return; //两个指针重合就返回,结束调用 int pivotIndex = QuickSort_Once(arr, begin, end); //会得到一个基准值下标 QuickSort(arr, begin, pivotIndex - 1); //对基准的左端进行排序 递归 QuickSort(arr, pivotIndex + 1, end); //对基准的右端进行排序 递归 } private static int QuickSort_Once(int[] arr, int begin, int end) { int pivot = arr[begin]; //将首元素作为基准 int i = begin; int j = end; while (i < j) { //从右到左,寻找第一个小于基准pivot的元素 while (arr[j] >= pivot && i < j) j--; //指针向前移 arr[i] = arr[j]; //执行到此,j已指向从右端起第一个小于基准pivot的元素,执行替换 //从左到右,寻找首个大于基准pivot的元素 while (arr[i] <= pivot && i < j) i++; //指针向后移 arr[j] = arr[i]; //执行到此,i已指向从左端起首个大于基准pivot的元素,执行替换 } //退出while循环,执行至此,必定是 i= j的情况(最后两个指针会碰头) //i(或j)所指向的既是基准位置,定位该趟的基准并将该基准位置返回 arr[i] = pivot; return i; } } } ``` ### 约瑟夫环 >0,1,,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。 例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。 **常规解法:** - 将[0,n]依次存储在链表中 - 只要链表的长度不为1,就一直循环,如果到了第m个就remove;否则将其添加到链表尾部 - 时间复杂度为O(nm) ``` java public int lastRemaining(int n, int m) { List<Integer> list=new ArrayList<>(); for(int i=0;i<n;i++) list.add(i); while(list.size()>1){ for(int j=0;j<m;j++){ if(j!=m-1) list.add(list.get(0)); list.remove(0); } } return list.get(0); } ``` **公式解法** - f(people,num) 表示在有people个人时,报数为num,胜利的人的位置 - people = 1 时, pos = 0 - pos=f(people,num)=(f(people−1,num)+num)%peoplepos = f(people,num) = (f(people-1,- num)+num)\% peoplepos=f(people,num)=(f(people−1,num)+num)%people ``` c++ class Solution { public: int lastRemaining(int n, int m) { int pos = 0;//1个人时 for(int i = 2; i <= n; i++) { //i表示人数 pos = (pos+m)%i; } return pos; } }; ```  ### 100层的楼,2个鸡蛋,如何最快测出哪层楼扔鸡蛋不会碎?时间复杂度是多少?平均时间复杂度? https://blog.csdn.net/qq_38316721/article/details/81351297 ### 判断一个点是否在三角形内 https://blog.csdn.net/IT_yanghui/article/details/83416129 ### 判断链表是否有环 https://blog.csdn.net/qq_32534441/article/details/88389223 ### 字符串翻转 ``` c #include <stdio.h> #include <string.h> #include <assert.h> void reverse_string(char *left, char *right) //连续的字符串逆序 { char temp; printf("\n");printf("\n");printf("\n"); printf("left:%s,right:%s",left,right); printf("\n"); while (right > left) { temp = *left; *left = *right; *right = temp; left++; right--; } printf("left:%s,right:%s",left,right); printf("\n"); } char *reserve(char *str) { assert(str); char *first = str; char *last = str + strlen(str) - 1; while (*str) { char *part = str; while (*str != ' '&&*str != '\0') { str++; } reverse_string(part, str - 1); if (*str != '\0') { str++; } else break; } reverse_string(first, last); return first; } int main() { char p[] = "student a am i"; printf("%s\n", reserve(p)); return 0; } ``` LeetCode 236 二叉树最近公共祖先: https://blog.csdn.net/jiangziya1713/article/details/105478334 ### AStar https://www.cnblogs.com/LiveForGame/p/10528393.html ### 动态规划 LeetCode 62:不同路径: https://blog.csdn.net/weixin_44547562/article/details/114236870 ### CodTop https://codetop.cc/home 数据结构与算法知识树整理——算法篇——基本算法思想 设计模式