菲涅尔方程(Fresnel Equation) agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/375746359) 菲涅尔效应 ----- 菲涅尔效应在我们的日常生活中无处不在,下面来个例子三连: 我们去公园的池塘喂鲤鱼,当爆米花丢的比较近的时候,我们可以看见水底下成群的鲤鱼在抢吃的。但是当我们把爆米花丢的很远时,却看不见水底下那些如狼似虎的鲤鱼,只能看见水面上的倒影。  我们在坐公交车的时候,从身边的窗户往外看,可以看清晰的看清楚车外的世界,但是当我们去看离得比较远的玻璃的时候,往往会看见很多车内的倒影,例如司机和别的乘客。  对于放置在桌面上的物体,当我们从不同的角度去观察它时,也会发现很神奇的现象,如下:  上面这些生活中常见的现象就是菲涅尔效应。 那么我们怎么用跟科学的术语来描述这个它们呢?我们能够看见水底下或者玻璃后的东西,那肯定是光线发生了**折射**所导致的。而对于水面上的倒影或者是玻璃变得像镜子一样这些都是因为光线发生了**反射**所导致的。通过前面的现象,我们可以发现,当我们人眼离物体表面(玻璃,水或者桌子等)比较近时,此时我们的**视线几乎与表面垂直**,我们可以看见更多折射过来的光(水底的鱼,玻璃外的东西)。而当们人眼离物体表面比较远时,此时我们的**视线几乎与表面平行**,我们可以看见更多反射过来的光(倒影)。 我们知道当光线打向一个物体表面(介质)时,会发生反射与折射。其中反射光的方向以及入射光的方向我们可以通过**反射定律**和**折射定律**来计算出。 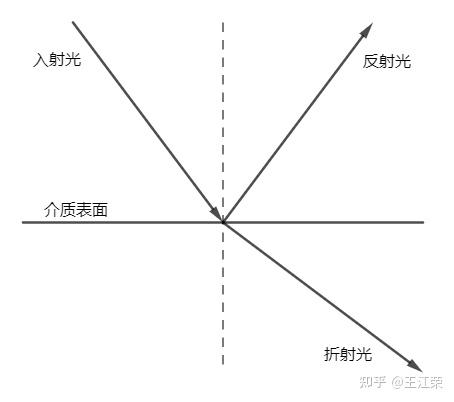 但是到底是反射光更强还是折射光更强呢?了解过辐射度量学应该知道这里比较的是辐射率(Radiance)的大小。通过菲涅尔效应我们不难发现,**当入射光方向接近垂直表面时,大部分的能量会被折射**,所以我们能看清水底的东西。而**当入射光方向接近平行表面时,大部分的能量会被反射**,所以我们会看见远处的倒影。 那么在我们渲染的时候,自然要把这个现象给考虑进去,才能够达到以假乱真的目的。因此我们自然需要一个公式,能够描述出在不同入射光的情况下,反射光与折射光所占的比例,这个公式就是菲涅尔方程。 菲涅尔方程 ----- 当光线碰撞到一个表面的时候,**菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比**。利用这个反射比率和能量守恒原则,我们可以直接得出光线被折射的部分以及光线剩余的能量。将其应用在 **BRDF** 当中,我们就可以更加精准的计算出渲染方程中  的值。 我们假设入射光与法线的夹角为  ,折射光与法线的夹角为  。由于折射还和介质的折射率有关,例如空气中的光射入水中,我们需要知道空气和水分别对应的折射率,我们再假设入射光所在介质的折射率为  ,物体的折射率为  。由于**光的偏振**(极化)现象,我们可以得到 S 偏振光 和 P 偏振光 分别对应的菲涅尔方程,如下: >  >  根据反射定律: >  可以推导出: >  因此上面的菲涅尔方程可以写成没有  的形式: >  >  如果我们不考虑偏振的情况,那么菲涅尔方程即是上面两者的平均值: >  利用菲涅尔方程,我们就可以根据不同的反射率画出 R 与  的对应关系图,如下: 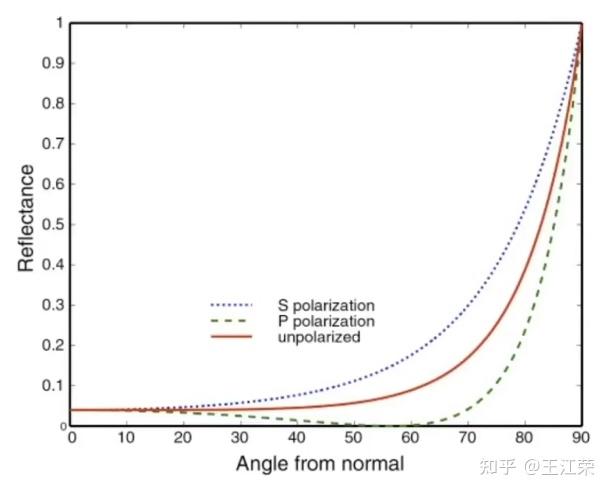 图中代表的是折射率为 1.5 的**绝缘体**(例如某种玻璃)的反射情况。可以发现当夹角为 0 时,即入射光垂直于表面,反射光的比例只有 4% 左右,而当夹角为 90 度时,即入射光平行于表面,反射比例将近 100%,符合我们前面所说的菲涅尔效应。 我们再来看一个**导体**(比如铜镜)的关系图,如下: 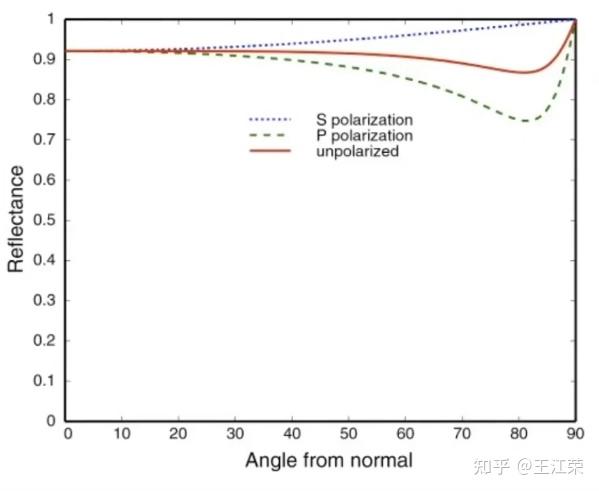 可以发现即使光线垂直于导体表面,但是依旧有 90% 的光被反射。这也证实了为什么我们可以用铜来做镜子,却没法使用玻璃来做镜子。 Schlick 近似法 ----------- 很明显,前面的式子实在太复杂了,计算量会非常的多,那么有没有什么近似的方法来求得菲涅尔方程的值呢? 从上面两个关系图中,我们可以发现,反射比例和夹角的关系,基本上都是由**基础反射率**(  的值,假设为  )以某种类似的曲线增长到 1。 其中基础反射率的值我们很好求得,因为此时  ,带入前面的公式可得: >  接下来的问题就是怎么用一个简单的函数使得反射率能随着  的增长以类似某种指数增长的方式从基础反射率变为 1,这里 **Schlick 为我们提供了一种近似方程**: >  注:其中  可以写成入射光方向和法线的点乘。 上面这个方程就是最终我们在渲染时常用的菲涅尔方程。用代码可以表示为: ``` vec3 fresnelSchlick(float cosTheta, vec3 R0) { return R0 + (1.0 - R0) * pow(1.0 - cosTheta, 5.0); } ``` 其中一个问题是它仅仅对电介质或者说非金属表面有定义,而对于导体表面,使用它们的折射率(导体的折射率为负数)计算并不能得出正确的结果。这样我们就需要使用一种不同的菲涅尔方程来对导体表面进行计算,但是这样很不方便。所以我们**预先计算出导体的基础反射率,**然后用 Schlick 方法来对其进行**插值**估算。这样我们就能对金属和非金属材质使用同一个公式了。 下面是一些常见材质的基础反射率: 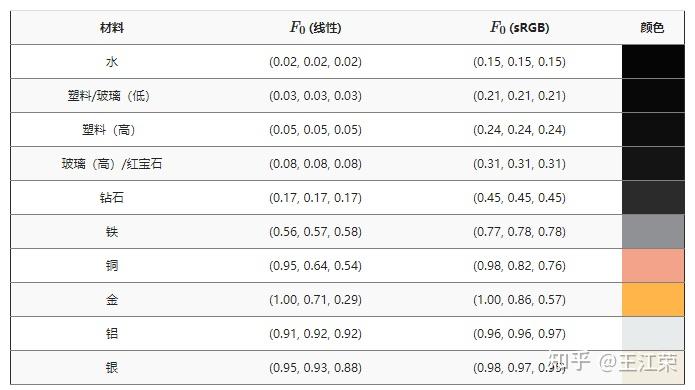 更多材质的基础反射率可以从下面网址查看: [RefractiveIndex.INFO - Refractive index database](https://refractiveindex.info/) 从中我们可以发现大多数电介质(绝缘体)的基础反射率要低于 0.17,而导体(金属)的往往在 0.5-1 之间。对于导体而言它们的基础反射率一般都是带有色彩的,这也是为什么要用 RGB 三原色来表示。 金属表面的这个特性也引出了所谓的**金属工作流**的概念。也就是我们需要额外使用一个被称为**金属度 (Metalness)** 的参数来参与编写表面材质。**金属度用来描述一个材质表面是金属还是非金属的。**理论上来说,一个表面的金属度应该是个布尔值,即要么是金属要么不是金属,不能两者皆是。但是,大多数的**渲染管线都允许在 0.0 至 1.0 之间线性的调配金属度**。这主要是由于材质纹理精度不足以描述一个拥有诸如细沙 / 沙状粒子 / 刮痕的金属表面。因此我们需要一个可调整的金属度模拟这些效果,来获得非常好看的视觉效果。 通过预先计算物体的基础反射率的值,我们可以对两种类型的表面使用相同的 Fresnel-Schlick 近似,但是如果是金属表面的话就需要对基础反射率添加色彩。我们一般是按下面这个样子来实现的: ``` vec3 R0 = vec3(0.04); R0 = mix(R0, surfaceColor.rgb, metalness);//根据金属度作插值 ``` 外发光 --- 根据菲涅尔效应我们可以知道,当物体表面的法线平行于屏幕的时候,也就是 Camera 基本水平看向这个表面的时候,此时的反射光应该是最强的,示意图如下:  因此我们就可以利用这个性质在 Shader 中制作外发光的效果,视频教程如下: [Unity Shader Graph 第二期:制作能量护盾_哔哩哔哩_bilibili](https://www.bilibili.com/video/BV1Fb411p7hN) 本文参考自: [GAMES101 - 现代计算机图形学入门 - 闫令琪_哔哩哔哩_bilibili](https://www.bilibili.com/video/BV1X7411F744?t=2777&p=17)[理论 - LearnOpenGL CN](https://learnopengl-cn.github.io/07%20PBR/01%20Theory/) 一些Unity面试题 SRP简单入门