贝塞尔曲线与曲面(Bezier Curve and Surface)的详细介绍与代码实现 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/366678047) 前言 -- 本文实在是有点长了,但是如果你坚持看完的话应该会对贝塞尔曲线和曲面有一个比较不错的了解(我自己是这样的)。同时学习完你还可以得到下面这样看着蛮有意思的效果,所以如果你有兴趣的话,那就坚持看完吧。  Demo 工程: [luckyWjr/Demo](https://github.com/luckyWjr/Demo)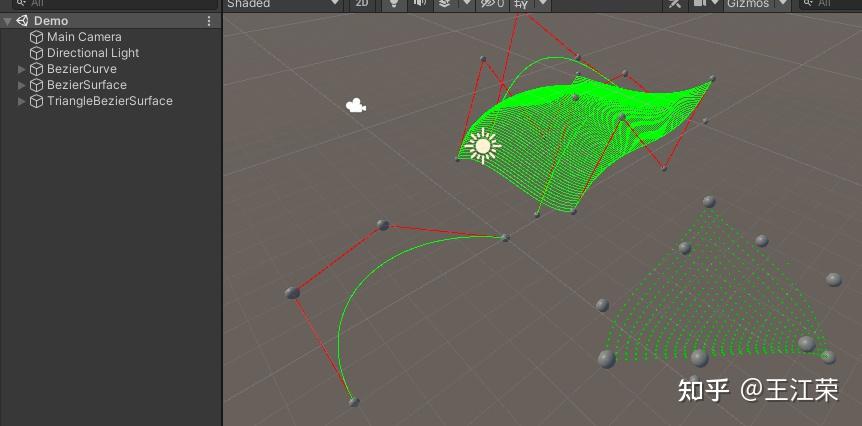 图形学为什么要曲线和曲面 ------------ 因为在生活中存在着各种各样光滑的曲线或曲面,例如汽车的表面,钢珠球等。  在建模的时候,我们通常使用很多的小三角形来逼近这样的曲面,因此放大了看,就会发现这些面其实是凹凸不平的。但是实际生活中,例如我们身边的杯子,无论怎么看它都是一个光滑的表面。 因此我们想要来表达出这样一种光滑的曲线或曲面,那么我们应该怎么表达这些光滑的曲线或曲面呢?我们先从曲线入手,看看它的几种表达方式。 曲线的显示表示(Explicit representation) -------------------------------- 学过函数我们知道,  画出来的图其实就是一条曲线,如下:  当然还有  等等函数,可以画出各式各样的曲线。这种 y=f(x) 的表达方式,我们称之为二维空间中曲线的**显示**表示。即**以自变量(x)来表达因变量(y)的值**。 曲线的隐式表示(Implicit representation) -------------------------------- 隐式表示,就是利用**隐式方程**来刻画一条曲线,在二维空间中一个隐式的曲线可以通过 f(x,y)=0 来表达。例如圆的隐式方程即为:  ,用它即可表示一个半径为 r 的圆。 曲线的参数形式表示(Parametric form) -------------------------- 该形式也是图形学里最关心和最常用的形式。一个曲线的参数形式是通过一个自变量(参数) t 来表达曲线上每个点的空间坐标,它也可算作是显示表示的一种。 在三维空间中,我们可以用如下三个显示的函数,来表示一条空间曲线。 * x=x(t) * y=y(t) * z=z(t) t=0 即代表曲线的起点,t=1 代表曲线的终点,因此可以用 t (0<=t<=1)代表曲线上的任意一点 P(t),然后将 t 的值带入三个显示的方程,即可求出曲线上点 P 的坐标: >  **参数曲线并不是唯一的**,一个给定的曲线或者曲面可以通过不同的形式表达。给定一个表达式我们可以画出一个唯一的曲线,但是该曲线可能还有别的表达式可以来表示。 参数形式有一个好处,例如上面的式子表达的是三维空间的曲线,如果我们删除了 z=z(t),那么它就变成了一个二维空间的曲线,即降维很方便。并且同样的也容易推广到高维,新增新维度对应的显示方程即可。 前面我们说了 t 的范围是 0-1,每个取值即代表曲线上的一点,那么我们只需要**将 t 的值慢慢从 0 变到 1 ,点就会沿着曲线行走,我们就可以得到曲线的轨迹,容易实现曲线的绘制**。 此外我们还可以对每个点求导,即  ,得到结果被视为曲线的**绘制速度**,该导数指向曲线的切向。 举个二维的例子,比方说我有一个  的曲线,其中 x 的取值范围为 1-4,那么这个曲线如下图: 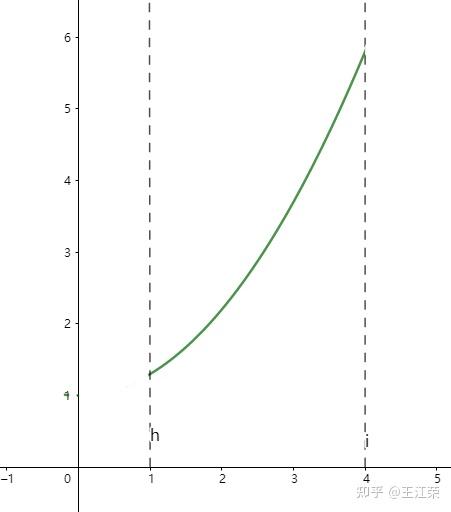 我们来看看怎么用参数的形式来表示它,首先是 x 和 t 的关系,因为 x 是 1 到 4,而 t 是 0 到 1,因此我们可得到方程 x = 3t+1 。然后是 y,因为我们知道这个曲线是  的,那么我们把里面的 x 用 x=3t+1 来代替即可,得到  。因此我们上诉曲线的参数形式即为: >  >  通过带入不同的 t 值,即可得到该曲线各个点的坐标,例如 P(0)=(1, 1.3),P(1)=(4, 5.8)。 参数形式与多项式 -------- 我们**曲线的参数形式写成一个多项式的形式**。例如我们前面的二维例子,我们可以把它写成一个二阶的多项式,即  的形式。但是**其中 a,b,c 并不是常数,而是代表着向量**,其结果为:  对于 3 阶多项式参数曲线具有如下形式: >  这样形成的曲线被称为 **Ferguson 曲线**,曾被用于美国早期的飞机设计中。 但是我们也可以发现,这种多项式的表达方式并不直观。而且 t 之前的系数也并不好算,即使给定了这些系数,也很难想象出曲线的形状。 因此后面就有了贝塞尔曲线。 贝塞尔曲线(Bezier Curve) ------------------- 相比之前的几种曲线表示方法,贝塞尔提出的是一种通过连接向量(connected vectors)来表示曲线的方法,如下:  即在画曲线前先通过向量绘制一个多边形,代表该曲线的趋势和走向。这就好比画画的时候先画个大致轮廓再画细节,雕刻的时候也是先雕个大致形状再慢慢打磨。 并且贝塞尔曲线具有**交互性**,也就是说我们可以通过修改向量,来修改曲线。 贝塞尔提出了如下公式用于计算曲线,将曲线表达成向量和基函数的乘积。 >  其中  代表的就是向量,  代表的是一个基函数,其内容如下: >  注:该基函数本质上就是一个 n-1 次的多项式。 有了这个公式后,也就是说你给我一个多边形,我就可以用它算出一个曲线,从公式中我们也可发现,**贝塞尔曲线属于一种参数形式(有参数 t)表示曲线的方式**。该公式简单了解下就行了,不需要去理解它,据说贝塞尔本人都说不清这个公式,很有意思哈哈。 伯恩斯坦多项式 ------- 1972 年,**Forrest** 在 Computer Aided Design 杂志上发表了他的著名论文,在论文里他指出**贝塞尔曲线可以借助伯恩斯坦多项式被定义在点集上**。 有关伯恩斯坦多项式的介绍可以参考,其中包括很多性质的推导: [王江荣:贝塞尔曲线中的伯恩斯坦多项式(Bernstein Polynomial)](https://zhuanlan.zhihu.com/p/366082920) 原本贝塞尔曲线说的是向量相连,我们现在把这向量都变成一个个控制点,即给定控制顶点  ,贝塞尔曲线上的任意一点  可以定义为: >  其中的  就是第 i 个 n 阶的伯恩斯坦多项式: >  其中  为组合数(排列组合的那个组合),它的值为: >  因为组合数有很多的性质,所以贝塞尔曲线的很多算法和定理,都是在弄这个组合公式。 伯恩斯坦多项式代码实现 ----------- 有了公式我们不就可以写出代码来了吗,下面是 Unity 的简单示例: ``` //伯恩斯坦多项式方法求曲线上一点 Vector3 GetCurvePointByBernstein(Vector3[] referencePoint, float t) { uint i = 0; int n = referencePoint.Length - 1;// n 阶是 n+1 个顶点 Vector3 point = Vector3.zero; for (; i <= n; i++) point += BernsteinNum(i, (uint)n, t) * referencePoint[i]; return point; } //伯恩斯坦多项式 float BernsteinNum(uint i, uint n, float t) { return CombinatorialNum(i, n) * Mathf.Pow(t, i) * Mathf.Pow(1.0f - t, n - i); } //组合数 ulong CombinatorialNum(uint i, uint n) { if (i > n) return 0; return Factorial(n) / (Factorial(i) * Factorial(n - i)); } //阶乘 ulong Factorial(uint n) { if (n == 0) return 1; ulong result = n; for (n--; n > 0; n--) result *= n; return result; } ``` 注:这里要注意的是公式里的 n 并不是说 n 个顶点,而是 0 到 n 一共 n+1 个顶点。还有代码就临时简单写的,也没优化,要是写的不好看别见怪!懂公式的话,很容易就能看懂。 这样我们就可以求出 t 从 0 到 1 所有曲线上的点,这些点就可以连成一条贝塞尔曲线。 德卡斯特里奥算法(de Casteljau Algorithm) -------------------------------- 但是实际上,我们并不会使用上面那个算法来求曲线上的任意点  ,而是使用一种名为 de Casteljau 的**递归算法**来求。该算法比之前的方法慢,但在**数值上更为稳定**。 接下来我们来看看用 de Casteljau 算法怎么求出曲线上的一点的。如下图,我们先随便选取三个控制点,并将它们前后连线。 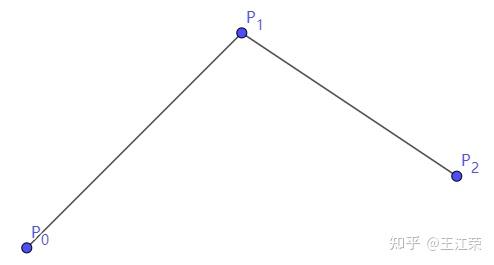 然后我们在  线段上通过**线性插值**在线段上找到点  ,使得  ,其他线段也如此,我们就可得到下图 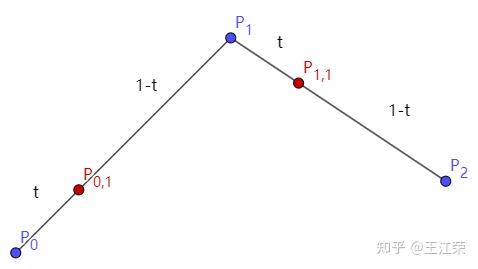 接着我们连接  ,得到新的线段,然后在该线段上再取一点使得该线段被分为 t 和 1-t,那么就会得到下图: 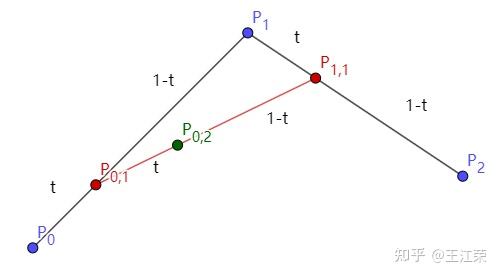 此时已经不能再连线了,而我们得到的点  就是这三个控制点对应的贝塞尔曲线在 t 位置上的点。 这样我们就可以通过使 t 从 0 变到 1,得到所有曲线上的点,从而得到曲线。这样的求曲线上任意一点方式也就是前面所说的 de Casteljau 算法**。** 如果有更多的控制点,我们也可以使用相同的方法来求出曲线上的一点,如下图是四个控制点求曲线上一点的过程: 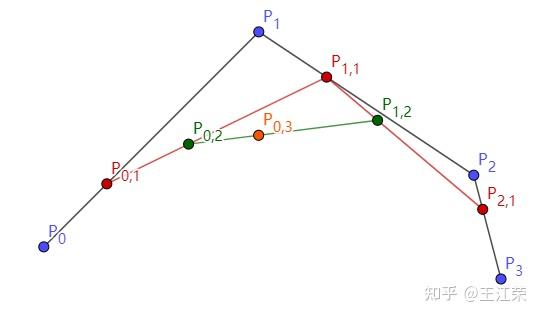 对于三个顶点控制的贝塞尔曲线我们称之为**二阶贝塞尔曲线(Quadratic Bezier)**,那么四个顶点自然是**三阶贝塞尔曲线(Cubic Bezier)**,因此 **n 阶贝塞尔曲线有 n+1 个顶点**。 而 de Casteljau 算法则是把这 n+1 个点,通过参数 t 用线性插值的方法,先变成 n 个新的点,然后在变成 n-1 个新的点,递归下去,最终得到一个点,这个点就是贝塞尔曲线上的点。 如下动图,很直接明了的表示了贝塞尔曲线的绘制过程: 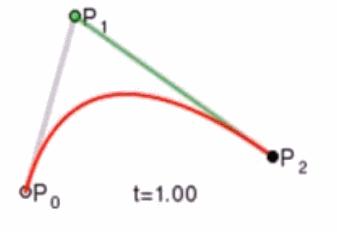 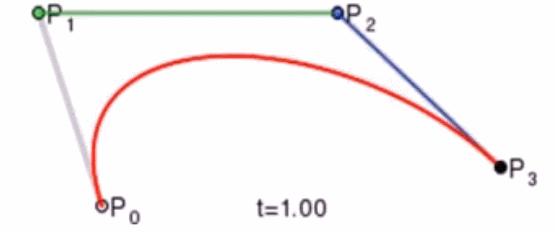 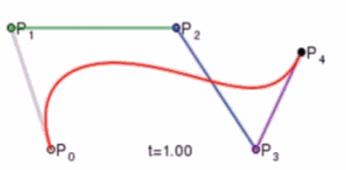 de Casteljau 算法代码实现 ------------------- 该算法看起来就和我们伯恩斯坦多项式没有任何关系了,我们只需要写个递归的方法,方法体内求线性插值即可: ``` //de Casteljau 算法求曲线上一点 Vector3 GetCurvePointDeCasteljau(Vector3[] referencePoint, float t) { int len = referencePoint.Length; if (len < 2) Debug.LogError("控制点至少需要两个"); Vector3[] newPoint = new Vector3[len - 1]; for (int i = 0; i < len - 1; i++) newPoint[i] = Vector3.Lerp(referencePoint[i], referencePoint[i + 1], t); if (len == 2) return newPoint[0]; else return GetCurvePointDeCasteljau(newPoint, t); } ``` 伯恩斯坦多项式与 de Casteljau 算法的关系 --------------------------- 回到公式部分,我们来看看伯恩斯坦多项式与 de Casteljau 算法的关系。我们拿最简单的二阶贝塞尔曲线举例,如下图:  图中蓝色的点为控制点,他们的坐标我们是知道的,那么通过线性插值,我们可以得到求出红色点的坐标,公式如下(  我们用  来代替): >  >  红色点坐标求出后,我们自然可以再求出绿色点的坐标: >  把上面两个式子带入到下面的式子,得到: >  我们还可以用这个方法去算三阶的,四阶的,乃至 n 阶的贝塞尔曲线,得到的结果为曲线上任意一点 P(t) 是各个顶点的线性组合,即:  而我们**每个顶点前面的系数 k,就是伯恩斯坦多项式**。例如二阶贝塞尔曲线对应的伯恩斯坦多项式为  ,其中  ,  ,  ,正好对应前面的三个系数。 因此可以得出结论,**对于 n 阶的贝塞尔曲线,曲线上 t 位置上的点 P(t) 的坐标是由 n+1 个顶点和伯恩斯坦多项式的乘积求和**: >  上面式子也就是 Forrest 在 1972 年提出的结论。 前面我们是从线性插值计算,**逆推**到伯恩斯坦多项式。现在我们来看看怎么直接使用伯恩斯坦多项式得到递归的结果。 注:下面公式看着都很长,其实都很简单,既没有微积分也没啥奇怪的公式,就是简单的加减乘除与一个插值的概念,所以看到它们的时候**不要怕!** 在讲到伯恩斯坦多项式的时候,我们说它具有递归性,即可以把 n 阶的伯恩斯坦多项式写成 n-1 阶的多项式组合: >  注:后面会写到很多伯恩斯坦多项式的性质公式,想了解的话还是建议看下之前的文章。 也就是说原本的方程式:  可以写成:  展开来,可得:  我们会发现里面有  ,我们提取一下不就变成了  ,而  是啥子?不就是**两点的线性插值**么。对于后面的几项也是一样的,上面式子就可以写成:  那么就可以把贝塞尔曲线的方程式写成: >  也就是说我们把原本 n 个控制点,通过  变成了 n-1 个新的控制点。那么 n-1 个控制点又可以按这个方法变成 n-2 个控制点,一直递归下去,最终只剩一个控制点,也就是曲线上的点。这个方法也正是我们之前贝塞尔曲线的绘制过程。 贝塞尔曲线的代码实现 ---------- 简单用 Unity 写了一下: ``` public class BezierCurve : MonoBehaviour { public Transform[] referencePointTransforms; public Transform curvePointTransform; Vector3[] mReferencePoints; int mSign = 1; float t = 0; int mResolution = 100; void Update() { TransformsToVectors(); t = Mathf.Clamp(t, 0, 1); // curvePointTransform.position = GetCurvePointDeCasteljau(mReferencePoints, t); curvePointTransform.position = GetCurvePointByBernstein(mReferencePoints, t); t += Time.deltaTime * 0.2f * mSign; if (t > 1 || t < 0) mSign *= -1; } void OnDrawGizmos() { TransformsToVectors(); if (mReferencePoints.Length == 0) return; //画控制点连线 Gizmos.color = Color.red; for (int i = 0; i < mReferencePoints.Length - 1; i++) Gizmos.DrawLine(mReferencePoints[i], mReferencePoints[i + 1]); //画曲线 Gizmos.color = Color.green; Vector3 start = mReferencePoints[0]; for (int i = 1; i <= mResolution; i++) { Vector3 end = GetCurvePointDeCasteljau(mReferencePoints, (float)i / mResolution); Gizmos.DrawLine(start, end); start = end; } } void TransformsToVectors() { int referencePointCount = referencePointTransforms.Length; mReferencePoints = new Vector3[referencePointCount]; for (int i = 0; i < referencePointCount; i++) mReferencePoints[i] = referencePointTransforms[i].position; } } ``` 效果图如下: 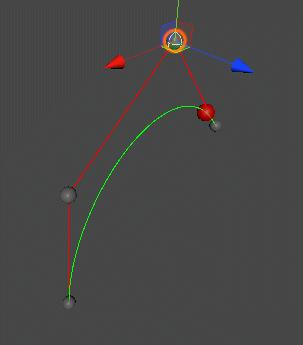 端点性质 ---- 伯恩斯坦多项式具有端点性质,贝塞尔曲线同样具有,其实从绘制过程中,我们就很容易看出来,曲线是从第一个控制点开始到最后一个控制点结束的,即: >  >  切向量(Tangent Vector) ------------------- 切向量也就是对贝塞尔曲线求导,我们知道伯恩斯坦多项式的求导公式如下: >  那么贝塞尔曲线的求导结果即为: >  我们先来看看 t=0 的情况,可得:  由于伯恩斯坦多项式的端点性质: >  所以  而  都为 0,可得: >  同理也可证明,当 t=1 时: >  也就是说贝塞尔曲线在起点处的切向量方向就是  到  的方向,终点处的切向量方向就是  到  的方向,如下图: 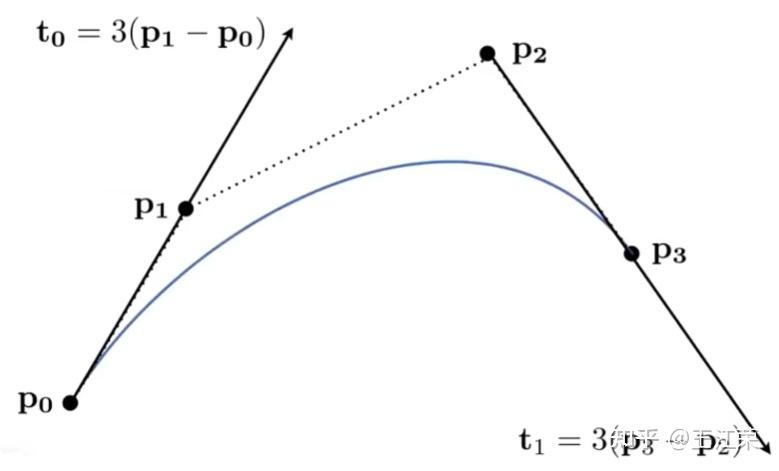 通过公式,也很好理解为什么三阶的贝塞尔曲线起点和终点的切向量前面有个系数 3 了。 二阶导数 ---- 同样的,我们还可以求贝塞尔曲线的二阶导数,公式如下(这里就不推导了,简单的记个笔记): >  因此: >  >  有了一阶和二阶导数,我们就可以算出曲率,**曲率是微分几何里面描述曲线弯曲程度的概念**。通过曲率公式可得: >  >  k 阶导数 ----- 贝塞尔曲线的 k 阶导数的差分形式如下: >   代表着 k 阶差分,定义如下: >  对称性 --- 因为伯恩斯坦多项式有对称性,因此贝塞尔曲线同样拥有对称性。也就是说我们把  这些顶点顺序倒过来,求得的曲线和之前的曲线一模一样,只是方向相反,如下图: 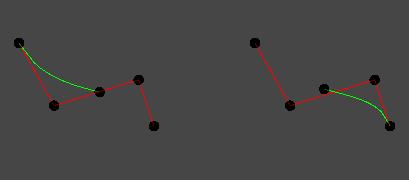 凸包性(Convex Hull) ---------------- 根据伯恩斯坦多项式的**归一性**,我们可以得出贝塞尔曲线的凸包性,也就是说**贝塞尔曲线必定在所有控制点的凸包内部。** 所谓**凸包即是可以包含所有顶点的最小凸多边形**,如下图:  黑色的点是我们的控制点,那么蓝色的形状就是这些控制点的凸包。我们可以把这些控制点想象成木板上的钉子,蓝色的线是一根可拉到无限大的橡皮筋,当我们把橡皮筋拉到包含所有顶点的时候,一松手,橡皮筋收缩后形成的形状就是凸包。 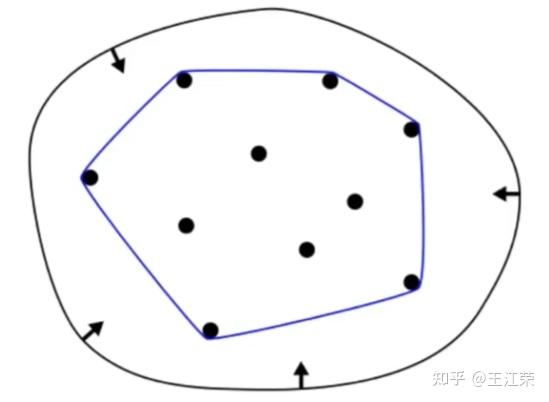 几何不变性(Geometric invariance) --------------------------- 即贝塞尔曲线的一些几何性质不随坐标系变换,因为贝塞尔曲线的位置和性质依赖于控制点,而不是坐标系。 仿射变换 ---- 对贝塞尔曲线做仿射变换,我们可以通过先对控制点做仿射变换,然后利用变换后的控制点来得到新的曲线,这个曲线和直接对曲线做仿射变换得到的结果是一样的。 但是需要注意,**透视投影变换不能这么操作**。 升阶操作 ---- 所谓升阶操作,就是比如我们原本由 n+1 个控制点得到一个 n 阶贝塞尔曲线,我们可以把它变成是 n+2 个新的控制点并且得到 n+1 阶的贝塞尔曲线,这两个曲线一模一样。 升阶操作的好处在于可以增加灵活性,例如我们原本有一个二阶的贝塞尔曲线,想要改变曲线形状只能修改三个顶点的位置。但是通过升阶,把它变成三阶的四阶的乃至更高阶的,我们就可以通过更多的顶点来调整这个曲线。 伯恩斯坦多项式的升阶公式如下: >  那么  就可以写成如下形式:  展开来看:  其中有  ,提取一下不就是  ,而  不就又是一个线性插值的点么,也就是升阶后的新点。往后也是,每两个控制点会线性插值出一个新的点,那么 n+1 个控制点不就可以生成 n 个新的控制点么。新的控制点  的公式如下: >  那么我们新的式子就可以写成: >  也就是说头尾两个控制点不变,中间生成 n 个新的控制点,这样原本 n+1 个控制点就变成了 n+2 个控制点,实现了升阶操作。 升阶公式最终如下: >  下图为升阶的效果图:  从图中可以发现,当升阶的次数越多,顶点形成的线条就会越逼近曲线本身。在微积分里有个 **Weierstrass 逼近定理**:一个连续函数总是可以用一个多项式无限逼近,我们的升阶操作就等于证明了这个定理(该定理本质上就可以用伯恩斯坦多项式来证明)。 但是这里其实有个问题,我们之前说切向量的时候,说贝塞尔曲线顶点和终点的切向量是第一个和最后一个控制点的方向。但是如上图,我们曲线没变,等于切向量没变,但是随着控制点增加,控制点的方向一直在变,这不是违背了么?实际上我们**将一个 n 阶的贝塞尔曲线升阶,不管升多少次,它本质上(代数上)还是 n 阶的,升阶只是给它换了个表现形式**。 降阶操作 ---- 降阶的目的是寻找一组新的控制点定义的曲线,使得误差最小。 降阶是升阶的逆过程,我们假设 n 阶贝塞尔曲线(控制点为  )是 n-1 阶贝塞尔曲线(控制点为  )的升阶结果,根据升阶公式我们可以得到: >  那么我们就可以得到下面两个递推公式(下面的公式 1 用  表示降阶后的顶点,公式 2 用  ): >  其中 i = 0, 1, ..., n-1 >  其中 i = n, n-1, ..., 1 这两个公式问题都很多,误差很大,公式 1 在  是精确的,越往后误差越大,而公式 2 在  是精确的,越往前误差越大。 因此 Forrest 提出的想法是,前半部分按第一个公式算,后半部分按第二个公式算,如下: >  后面 Farin 提出一个想法,把这两个公式线性插值一下,如下: >  到这基本就把贝塞尔曲线和它的性质,操作给介绍的差不多了,实在是太多公式了~ 长须一口气,huuuuuuuuuuuuuuuuuuu~ 逐段的贝塞尔曲线(Piecewise Bezier Curves) --------------------------------- 我们看看贝塞尔曲线存在的一些问题,如下图一个十阶的贝塞尔曲线 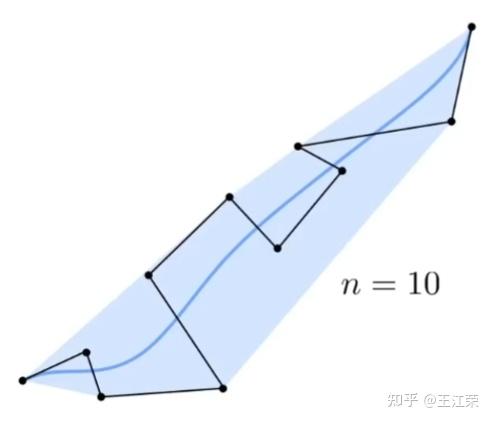 这里会存在一些问题: * 首先二阶三阶的贝塞尔曲线我们很容易通过控制点就想象出曲线的大致形状,但是**当控制点很多的时候,我们很难想象出曲线大致的形状**。 * 其次我们无法做到只修改曲线的某一部分,因为**只要动一个控制点,整个曲线都会跟着发生变化**,正所谓牵一发而动千身。 * 高阶的贝塞尔曲线往往会导致**拐来拐去的**,导致并不光滑,但是例如飞机汽车的表面都是很光滑的。 因此在 CAD 的应用中,通常不鼓励使用高阶的贝塞尔曲线,而是使用低阶贝塞尔曲线(通常用四阶的)相连,如下图: 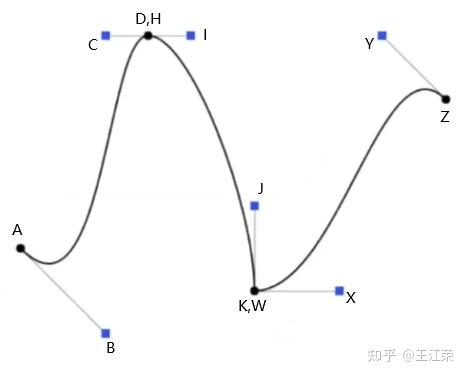 如图,由三段四阶的贝塞尔曲线连成(是不是很像 PS 的钢笔工具),分别是 ABCD,HIJK 和 WXYZ 三组控制点。 连续性 --- 如上图,在 K(或 W)点有很明显的拐点,这种现象我们称之为不连续。**在微积分的观念里,我们对曲线上的某一个点左右求导,如果导数相等,那么就是连续的**,对于这种连续性我们称为**传统的连续性**。那么对应 K(或 W)点的左右导数根据贝塞尔曲线导数的性质我们很容易就得到 3(K-J) 和 3(W-X),很明显是不相等的,所以不连续。 但是这里我们可以举一个反例,如下图:  我们以 AB 两点作为控制点形成贝塞尔曲线,那么该曲线自然就是 AB 线段,同样的,我们以 BC 两点再形成一个贝塞尔曲线为 BC 线段,AB 和 BC 形成一条直线段。此时 B 点左右的导数分别为 (B-A) 和(C-B),这两个值明显是不相等的,按微积分里的定义就是不连续。可是它明明是一条直线,怎么会不连续呢?这个反例意味着传统的连续性不适用于描述 CAD 和图形学中形状的连续性,因此提出了**几何连续性**(Geometric continuity)的概念。 所谓几何连续性的概念,就是导数的方向一样,我们即可认为是连续的。对于例子中的直线,我们认为它是几何连续的,但是速度不一样,例如一个小蚂蚁在 ABC 上爬,在 AB 上较慢,在 BC 上变快了。 那么我们就有如下定义,假设我们有  和  形成的两条贝塞尔曲线,如果: >  ,我们称之为 **0 阶连续,标记为**  或  。 >  ,且这四个点共线,我们称之为 **1 阶几何连续**,如果 k=1,那么就是 **1 阶连续,标记为** 或  。 > 如果二阶导数相等,即曲率连续,我们称之为 **2 阶连续,标记为** 或  。 连续性的效果如下([http://math.hws.edu/eck/cs424/notes2013/canvas/bezier.html](http://math.hws.edu/eck/cs424/notes2013/canvas/bezier.html)): 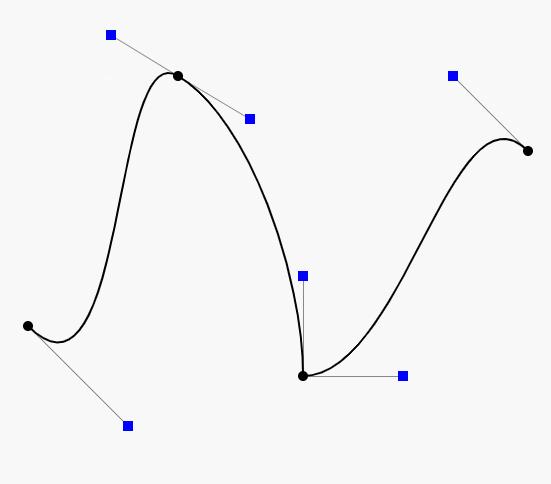 贝塞尔曲面 ----- 我们接下来看看下面这种情况: 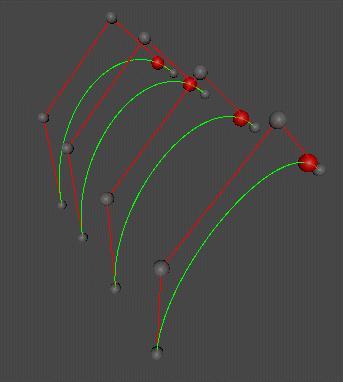 如图,我们有四条一模一样的贝塞尔曲线,图中的小红点是这些曲线在 t 从 0 到 1 变化时对应的点。 那么假如我们现在把这些小红点互相连线,会形成啥呢?想象一下,没错,就是一个曲面!如下图: 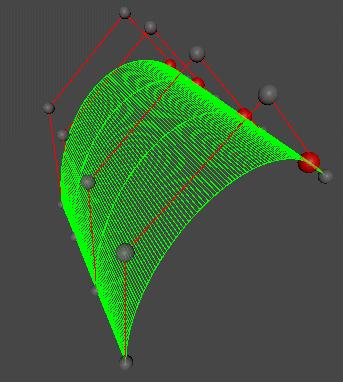 噢!这该死的摩尔纹!!! 但是这样形成的曲面其实有很大的问题,它仅仅**只是在一个方向上弯曲**,在与其垂直的方向上依旧还是笔直的,如果我们简单修改下控制点的位置,就会出现下面这样的问题: 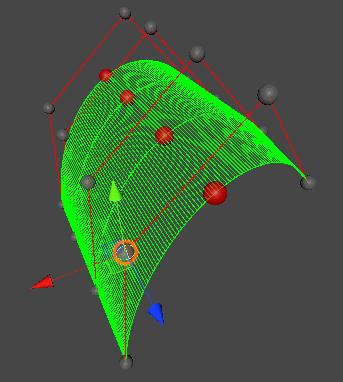 那么我们就要想办法优化它,人们想到,如果**用这个四个小红点再做控制点**,不就可以在垂直方向上又形成一条光滑的曲线了么? 没错,这就是贝塞尔曲线的思路,我们先用一组贝塞尔曲线在 t1 位置得到一组对应在曲线上的点,然后将这些点再作为控制点来做曲线,所有的曲线组合起来,即可得到一个光滑的曲面。 效果图如下:  图中可以发现,不管我们怎么修改控制点,都可以得到在所有方向上都是光滑的曲线。 害,要不是因为曲面的示意图少,我也不用专门写代码来展示了!!!瞎鸡儿写一下的代码如下: ``` public class BezierSurface : MonoBehaviour { public BezierCurve[] curves; int mResolution = 100; void OnDrawGizmos() { Gizmos.color = Color.green; for (int i = 1; i <= mResolution; i++) { //获取每个曲线上 t 时刻的点 Vector3[] curvePoints = new Vector3[curves.Length]; for (int j = 0; j < curvePoints.Length; j++) { Vector3[] referencePoint = GetCurveReferencePoint(curves[j]); curvePoints[j] = GetCurvePointDeCasteljau(referencePoint, (float)i / mResolution); } //根据上面获得的点再画曲线 Vector3 start = curvePoints[0]; for (int j = 1; j <= mResolution; j++) { Vector3 end = GetCurvePointDeCasteljau(curvePoints, (float)j / mResolution); Gizmos.DrawLine(start, end); start = end; } // 那些点直接连线的错误示范 // Vector3 start = curvePoints[0]; // for (int j = 1; j < curvePoints.Length; j++) // { // Vector3 end = curvePoints[j]; // Gizmos.DrawLine(start, end); // start = end; // } } } Vector3[] GetCurveReferencePoint(BezierCurve curve) { Vector3[] array = new Vector3[curve.referencePointTransforms.Length]; for (int i = 0; i < array.Length; i++) array[i] = curve.referencePointTransforms[i].position; return array; } } ```  原理知道了,接下来我们看看怎么求贝塞尔曲面上任意一点,以及贝塞尔曲面的一些性质。 又到了密密麻麻又枯燥的公式部分了(其实公式一点也不枯燥,专研起来很有趣的,就是看着确实很头疼)。 贝塞尔曲面上的任意一点 ----------- 首先我们有一个 n 阶的贝塞尔曲线,然后我们给它复制 m+1 份,那么在每个贝塞尔曲线的 t1 位置,我们可以得到 m+1 个曲线上的点。我们再把这些点作为控制点,可以得到一个 m 阶的贝塞尔曲线,而这个贝塞尔曲线就是最终贝塞尔曲面上的一条线,因此该曲线 t2 位置上的点就是贝塞尔曲面上的点。其中 t1 和 t2 通常会使用 u 和 v 来代替,它们的取值范围自然都是 0 到 1,那么对应贝塞尔曲面上的任意一点,我们就可以用 P(u,v) 来表示。 对于上面这种描述得到的曲面,我们**称之为 m*n 阶的贝塞尔曲面,即有 m+1 条 n 阶的贝塞尔曲线,一共会得到 (n+1)*(m+1) 个顶点**,这里我们定义第一个 n 阶的贝塞尔曲线的第一个控制点为  ,该曲线往后的控制点为  ,那么第 i 条 n 阶的贝塞尔曲线的第 j 个顶点就是  ,最后一条的最后一个顶点自然是  了。 要求贝塞尔曲面上的一点,我们先来复习一下贝塞尔曲线上一点的公式(毕竟文章稍微有点长了,在往上翻去找有点费劲): >  那么第 i 条 n 阶的贝塞尔曲线上的点 P(u) 即为: >  那么我们就可以得到 m 个 P(u),我们可以标记为  ,这些 P(u) 会再形成贝塞尔曲线,也就是曲面上的曲线,那么该曲线上的点 P(v) 即为: >  那么两个公式合起来,就是我们求贝塞尔曲面上任意点 P(u,v) 的公式了: >  此外,我们还可以用矩阵的形式来表示,如下: >  简单的解读下,首先是 1*(n+1) 的矩阵乘以 (n+1)*(m+1) 的矩阵,得到的结果是 1*(m+1) 的矩阵,这一步其实就是在求 m+1 条贝塞尔曲线 u 位置的顶点。然后把 1*(m+1) 的矩阵再乘以 (m+1)*1 的矩阵,得到的结果就是一个值,这一步就是求新的曲线在 v 位置上的点。 当然了,同样的,我们**也可以用 de Casteljau 算法来算曲面上的任意一点的坐标**。 端点性质 ---- 控制网格的四个顶点同样是贝塞尔曲面的顶点,即: >  >  >  >  切平面 --- 以下三角形指定了贝塞尔曲面四个角的切平面: >  >  >  >   此外,贝塞尔曲线带有的凸包性,对称性,几何不变性,在贝塞尔曲面中也都有这些性质。 连续性 --- 首先要两个贝塞尔曲面连续,它们的控制顶点数必须相同,不然一个 9 个点的曲面和一个 16 个点的曲面,很难做到连续。因此对与连续性,我们只考虑两个曲面控制顶点相同的情况。  假设有两个 m*n 阶的贝塞尔曲面,它们的控制顶点分别是  和  那么 **0 阶连续(** 或  **)**的表示如下: >  i = 0,1,...,m 这个式子很好理解,就是我们第一个贝塞尔曲面的每条贝塞尔曲线的最后一个控制点要和另一个贝塞尔曲面的每条贝塞尔曲线的第一个控制点重叠。 每个控制点都一样,那么得到的曲线也都一样,所以曲线上对应 v 位置的点也都一样,所以也可以写成如下形式: >  我们用之前的烂代码在 Unity 模拟一下,如下图,是两个 3*3 阶的贝塞尔曲面,我们使头尾控制点位置相同,图中圈起来的地方  然后我们不管怎么移动其他控制点,链接处都保持这一样的曲线,这种就是所谓的 0 阶连续  而对于 **1 阶连续(** 或 **)**,同样是对切向量进行限制。为了方便理解,我们举个例子,如下图:  红点是我们两个曲面连接的控制点,我们来看  这个点。首先我们知道这个点会有如下两个切线,一个是  方向的,一个是  方向的。其次由于小红点又形成了贝塞尔曲线,因此在小红点这个方向上  还有个切线,即  。因为四个小红点本身形成的就是一个光滑连续的曲线,所以在这个方向上,一个点不会存在左右两个不同的切线。所以**在两个曲面的连接处上的任意一点,我们其实可以得到三个切线**。而**只要这三个切线共面,我们就称之为一阶几何连续**。如果除了小红点方向的切线,另外两个切线的值相等方向相反的话,那么就是一阶连续。 三角域贝塞尔曲面 -------- 前面介绍的贝塞尔曲面我们称之为**矩形域贝塞尔曲面**,u 和 v 都是 0 到 1,定义在矩形上。接下来我们介绍一下定义在三角形上的贝塞尔曲面,也就是**三角域贝塞尔曲面**。 没错,又要用到重心坐标了,再次发下自己的之前的链接,嘿嘿 [王江荣:直线与三角形的重心坐标(Barycentric Coordinates)的推导与应用](https://zhuanlan.zhihu.com/p/361943207) 我们知道三角形上任意一点,我们可以用 (u,w,w) 的坐标来表示,其中 u+v+w=1,这个表示方式就是重心坐标。 如下图,如果我们只有如下三个顶点,那么每条边自然都是直线,形成的也就是个三角形平面。  但是如果每条边变成多个顶点呢?如下图,那么每条边不就可以由这些顶点变成一条贝塞尔曲线了么。  三条边变曲线好搞,我们要怎么让整个三角形面都变成光滑的曲面么?一样的思路,我们要求出三角形内任意一点的坐标,利用重心坐标,我们对三角形内任意点记作 P(u,v,w) 。 然后我们再定义一些规范,首先每条边的顶点数要相同,不能一条边 4 个顶点,一条边 10 个顶点,这不是为难人嘛。如果**每条边都有 n+1 个顶点,我们称之为 n 阶的三角域贝塞尔曲面**。 为了方便理解,我们首先假设每条边被各自的顶点分成了等长的线段,那么我们就可以求出每个顶点的重心坐标了(至于哪个顶点对应 u,哪个对应 v,哪个对应 w,随你喜欢),如下:  **得到重心坐标后,我们把这些值同时乘以阶数 n ,得到的值就作为控制点的下标。**例如上图中三角形是 3 阶的,那么就把这些重心坐标的值都乘以 3,例如重心坐标为 (1/3, 0, 2/3) 的控制点,乘以 3 后为(1,0,2),那么该控制点就标记为  ,这样我们可以得到下图:  也就是说我们控制点可以用  来表示,其中 i+j+k=n,这其实就是我们三角域的伯恩斯坦多项式(不熟悉的请看伯恩斯坦多项式的文章最后的介绍),因此对于三角域贝塞尔曲面上的任意一点 P(u,v,w) 我们可以得到这样一个公式: >  其中 i 的取值范围为 0 到 n,j 的取值范围为 0 到 n-i,i 和 j 确定后,k 也就确定了,因此我们还可以写成下面这个形式: >  而  就是我们的三角域伯恩斯坦多项式,其值为: >  但是我们知道  应该是有  项的,也就是说对于上面我们 n=3 的三角形,应该有 10 个  顶点,但是上面数来数去只有 9 个,因为少了  ,我们把它补上(对于更高阶的三角形,要补得顶点会更多),如下图:  代码实现 ---- 有了公式我们就可以写代码了(依旧简单的写一下,写的不好别见怪) ``` [Serializable] public struct TriangleReferencePoint { public string ijk; public Transform trans; public bool isEqual(uint i, uint j, uint k) { uint num = uint.Parse(ijk); if (100 * i + 10 * j + k == num) return true; return false; } } public class TriangleBezierSurface : MonoBehaviour { public uint n = 3; public TriangleReferencePoint[] referencePoints; int mResolution = 30; Vector3[,,] PointsToVector3s() { Vector3[,,] array = new Vector3[n + 1, n + 1, n + 1]; for (uint i = 0; i <= n; i++) { for (uint j = 0; j <= n-i; j++) { uint k = n - i - j; array[i, j, k] = FindReferencePoint(i, j, k).trans.position; } } return array; } TriangleReferencePoint FindReferencePoint(uint i, uint j, uint k) { foreach (var point in referencePoints) { if (point.isEqual(i, j, k)) return point; } Debug.LogError("没找到对应控制点,错误的控制点下标"); return new TriangleReferencePoint(); } void OnDrawGizmos() { if ((n + 1) * (n + 2) / 2 != referencePoints.Length) { Debug.LogError("顶点数不匹配"); return; } Gizmos.color = Color.green; Vector3[,,] referencePointPositions = PointsToVector3s(); float u, v, w; uint i, j, k; float step = 1.0f / mResolution; //取重心坐标 for (u = 0; u <= 1.0f; u += step) { for (v = 0; v <= 1.0f - u; v += step) { w = 1.0f - u - v; //利用三角域的伯恩斯坦多项式,计算每个(u,v,w)对应的曲面上的点P(u,v,w) Vector3 p = Vector3.zero; for (i = 0; i <= n; i++) { for (j = 0; j <= n - i; j++) { k = n - i - j; p += TriangleBernsteinNum(i, j, k, n, u, v, w) * referencePointPositions[i, j, k]; } } Gizmos.DrawSphere(p, 0.02f); } } } //三角域的伯恩斯坦多项式 float TriangleBernsteinNum(uint i,uint j,uint k, uint n, float u, float v, float w) { return TriangleCombinatorialNum(i, j, k, n) * Mathf.Pow(u, i) * Mathf.Pow(v, j) * Mathf.Pow(w, k); } //三角域的组合数 ulong TriangleCombinatorialNum(uint i,uint j,uint k, uint n) { if (i + j + k != n) return 0; return Factorial(n) / (Factorial(i) * Factorial(j) * Factorial(k)); } //阶乘 ulong Factorial(uint n) { if (n == 0) return 1; ulong result = n; for (n--; n > 0; n--) result *= n; return result; } } ```  我们来看看得到的效果:  很骚有没有!!! 三角域贝塞尔曲面的 de Casteljau 算法 ------------------------- 前面我们知道三角域的贝塞尔曲面上的任意一点定义如下: >  我们把它展开来可以得到下面式子(注:为了简洁,就省略伯恩斯坦多项式里带的 (u,v,w) 了): >  然后我们来看看三角域伯恩斯坦多项式的递归公式: >  带入上面公式,得到:  我们会发现里面有这么三项相加:  我们提取一下不就变成了:  括号里的不就是  三角形内的一点嘛。 我们最终可以得出,如果 n 阶的三角形(其控制点为 )变成 n-1 阶的三角形(其控制点为 ),那么有如下关系: >  这样一直递归下去,最终会得到只剩一个点,那么这个点就是这个三角域贝塞尔曲面上的点。 有点难懂?我们来看下示意图,前面我们有一个 3 阶的三角形,那么降阶后就会变成一个二阶的三角形,如下图,红色点就是降阶后得到的新的控制点:  每个红色控制点都是通过它周边三个蓝色控制点利用重心坐标所得到的。 然后这个红色 2 阶三角形我们还可以再降阶,得到绿色的三角形,如下图:  图中绿色的点就是 1 阶三角形的三个控制点,同样是通过边上三个红色控制点利用重心坐标得到的。 到了这一步,我们就不能降阶了,那么再利用重心坐标求出绿色三角形内的那个点,就是最终曲面上的点,是不是很有意思。 de Casteljau 算法代码实现 ------------------- 同样我们用 Unity 简单的实现下这个算法,很简单,就是个递归而已。 ``` //记录当前的阶数 uint currentN; //de Casteljau 算法求曲面上一点 Vector3 GetSurfacePointDeCasteljau(Vector3[,,] referencePoint, float u, float v, float w) { currentN--; Vector3[,,] newReferencePoint = new Vector3[currentN + 1, currentN + 1, currentN + 1]; for (uint i = 0; i <= currentN; i++) { for (uint j = 0; j <= currentN - i; j++) { uint k = currentN - i - j; newReferencePoint[i, j, k] = u * referencePoint[i + 1, j, k] + v * referencePoint[i, j + 1, k] + w * referencePoint[i, j, k + 1]; } } if (currentN == 0) return newReferencePoint[0, 0, 0]; else return GetSurfacePointDeCasteljau(newReferencePoint, u, v, w); } ``` 然后修改下绘制取点的方法即可,如下: ``` //取重心坐标 for (u = 0; u <= 1.0f; u += step) { for (v = 0; v <= 1.0f - u; v += step) { w = 1.0f - u - v; //de Casteljau currentN = n; Vector3 p = GetSurfacePointDeCasteljau(referencePointPositions, u, v, w); Gizmos.DrawSphere(p, 0.02f); } } ``` 就可得达到和之前伯恩斯坦多项式算法一样的效果了。 三角域贝塞尔曲面转换为矩形域贝塞尔曲面 ------------------- 简单的介绍下,不是专业搞这个的话,跟我一样听个响就行了~ 其中一种转换方法如下图:  右图可以看出,虽然有条边依旧是一个顶点,但是其他几条边都变成了 n+1 个顶点,该操作是利用**升阶**来完成的。 例如图中,我们三角形最下面是 4 个顶点,那么转到矩形域保持不变,然后再往上是 3 个顶点,我们进行一次升阶操作,不就变成 4 个顶点了嘛。再往上是两个顶点,我们进行两次升阶操作,又变成 4 个了。最后 1 个顶点,不管怎么升阶还是 1 个,因此就可以得到右边的图像。 另外一种方法是:在三角形中间取一点,把三角形分成四个矩形,如下:  目前个人对贝塞尔曲线和曲面了解的就这么多了~ 谢谢阅读。此外如今还有更加牛逼的 **B - 样条曲线**(B-spline curve),当然也更加的复杂。 贝塞尔曲线中的伯恩斯坦多项式(Bernstein Polynomial) 光栅化与深度缓存