贝塞尔曲线中的伯恩斯坦多项式(Bernstein Polynomial) agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/366082920) 在学习贝塞尔曲线的时候,大家一定都听过一个词叫伯恩斯坦多项式,我们先从一个简单的例子来看看它到底是什么。 [王江荣:贝塞尔曲线(Bezier Curve)](https://zhuanlan.zhihu.com/p/366678047) 本文主要参考清华大学胡事民教授的课件,也算当了回清华学生了,哈哈~ [清华大学 - 计算机图形学基础(国家级精品课)_哔哩哔哩 (゜ - ゜) つロ 干杯~-bilibili](https://www.bilibili.com/video/BV13441127CH?t=2447&p=11) 开礼包的概率 ------ 现在在各种游戏里,肯定都会充斥着开礼包的骗钱玩法。拿我玩的某刀举例,我们有 0.1 的概率开到高级物品,假设我们有 3 个这样的礼包,那么我们可以得到如下一些结果: 首先是拿命玩游戏的人,开到 3 个高级物品,这个概率想求很简单,自然是  。 其次是还能活几天的人,开到 2 个高级物品,那么这个概率是多少呢?我们知道开到的概率是 0.1,那么开不到的概率自然是 1-0.1=0.9。那么开到两个的概率是  ,一个没开到的概率是 0.9,总的概率是  嘛?错!在这里还存在着排列组合的关系,例如我前两个开到后一个没开到,它的概率是  ,而我第一个没开到后两个开到,它的概率是  ,当然还有中间没开到前后开到的情况,这些三种情况都属于开到 2 个高级物品,因此总概率应该为  。 然后是欧皇,开到 1 个高级物品,一样存在排列组合的情况,概率应该为  。 最后是正常人,一个都开不到,这个概率自然是  。 题外话:非酋,我,连续二十几次没开到,概率为 0!!!严重怀疑程序有 bug。 而**这些概率相加得到的结果自然是 1**。不存在 200% 这种概率啊。 伯恩斯坦多项式 ------- 通过上面的例子,我们可以假设有个礼包开到东西的概率为 t ,我们一共开 n 次,那么开到 i 次东西的概率应该怎么计算呢? i=n 很好算,自然是  ,同样 i=0 也很好算,自然是  ,相对麻烦的是中间,因为我们前面说了,需要考虑到排列组合的情况,当然不管怎么排列组合,每个组合的概率应该都是  。 接下来的问题就是算开到 i 次时,存在多少排列组合的情况了(假设值为 k)。怎么算呢,其实[百度百科](https://baike.baidu.com/item/%E6%8E%92%E5%88%97%E7%BB%84%E5%90%88/706498?fr=aladdin)上有公式,如下: >  注:规定  ,因此即使 i=0,除数不会为 0。 简单的理解下,我们可以把问题想成,我们有 i 个开到的礼包,要插入到这 n 个位置里,那么当我插入第一个礼包的时候,有 n 个空位给我放,插入第二个的时候,有 n-1 个空位,直到差到第 i 个,有 n-i+1 个空位,那么得到的结果就是:  但是这里面还存在重复的情况,例如我第 1 个礼包放 1 号位,第 2 个礼包放 2 号位,和第 1 个礼包放 2 号位,第 2 个礼包放 1 号位是一样的,因此我们要去重。i 个礼包一共会有 i! 次情况,因此最终会得到上面的排列组合结果。 当然了,i=0 或者 i=n 同样适用于这个公式,因此开到 i 次东西的概率应该为: >  这个其实就是我们要说的伯恩斯坦多项式! 我们常用  或者  来代表伯恩斯坦多样式,其中  部分我们常用  或者  来代替。 **因此伯恩斯坦多项式可以表示为:** >  或者 >  **其中 n 为非 0 正整数,i 的取值范围为 0-n,t 的取值范围为 0-1 。** 如图是 n=10,i=3 的伯恩斯坦多项式曲线图: 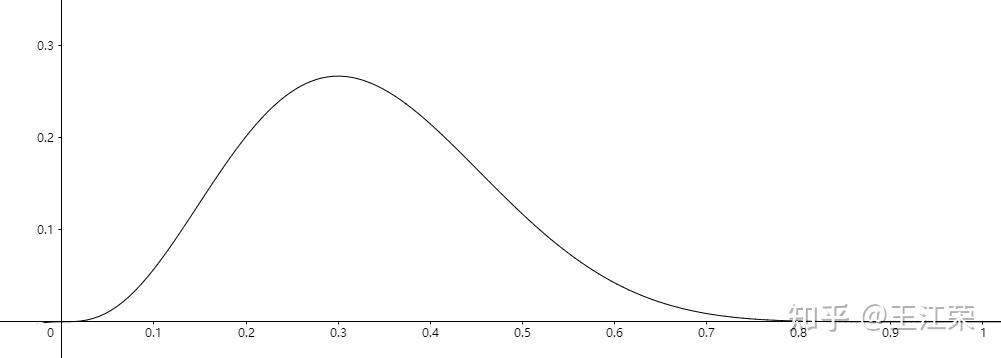 从曲线可以看出,在 t=0.3 处会有一个极大值,并向两边衰减,并且所有的伯恩斯坦曲线都有类似的性质。这个情况用常识也很好理解,如果我们想要从 10 次开出 3 次,那么从统计学来说只有概率等 0.3(i/n)时,开出 3 次的概率最高。后面会用导数来证明。 **贝塞尔曲线,就是使用伯恩斯坦多样式来定义。因此它的一些性质同样会影响到贝塞尔曲线的性质**,我们接下来看看伯恩斯坦多项式有哪些性质。 非负性(Non-negative) ----------------- 当我们 t=0 时,  ,当 t=1 时,  ,因此  。而当 0<t<1 时,  。 因此具有非负性: >  端点(End point) ------------- 当我们概率为 0,即 t=0,那么开到 0 次(即 i=0)的概率肯定也为 1 ,而开到其他次数的概率肯定为 0,可得: >  当我们概率为 1,即 t=1,那么开到 n 次(即 i=n)的概率肯定也为 1 ,而开到其他次数的概率肯定为 0,可得: >  也就是说当 t=0 时,只有 i=0 这一项有意义(等于 1),其他项都为 0。而当 t=1 时,也只有 i=n 这一项有意义(等于 1),其他项也都为 0 。 归一性(Unity) ---------- 伯恩斯坦多项式的**求和等于 1**,在前面开礼包的例子里,我们已经提到了,所有概率加起来等于 1。我们现在在代数的形式上证明一下: 首先  ,而  正好是一个**二项展开式**。 什么是[二项展开式](https://baike.baidu.com/item/%E4%BA%8C%E9%A1%B9%E5%B1%95%E5%BC%80%E5%BC%8F/7078006?fr=aladdin)?我们知道  , (这个正好就是我们文章开头例子的算法)等等,这些就是我们的二项展开式。 那么  是多少呢?正是上面的  ,其中 a=t,b=1-t,因此: >  对称性(Symmetry) ------------- >  我们也可从下图曲线看出其对称性: 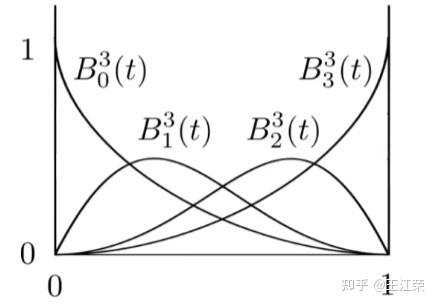  和  对称,  和  对称,即**第 i 个和倒数第 i 个是对称的**。 证明:   两者相等。 递归性(Recursive) -------------- 递归性是什么意思呢,就是说一个 n 阶的伯恩斯坦多项式  ,它可以写成两个 n-1 阶的伯恩斯坦多项式的组合,即: >  很多贝塞尔曲线的定理和证明里都是做这个组合公式的应用。 证明: 首先:  上面式子也是排列组合的基本性质,常用于杨辉三角。   有个很聪明的理解方法:  即 n 里面取 i 个,那么我们可以拆分成: * 从 n-1 个里面取 i 个并且从 1 个里面取 0 个,那么对应的就是  * 从 n-1 个里面取 i-1 个并且从 1 个里面取 1 个,那么对应的就是  这两个步骤合在一起不就是从 n 里面取 i 个嘛。 然后我们可以得到:  然后就变成了  左项提取 1-t,右项提取 t,即可得到我们最上面的式子。 这里还有个问题,即 i=0 怎么办?那 i-1 不就等于 -1 了。对于该情况,式子如下: >  我们可以这么理解:  不就等于  ,不就等于  ,而  正是  ,所以可以得到如上式子。 同样的 i=n 的时候会出现  的情况,和上面一样理解即可  ,因此: >  导数(Derivation) -------------- >  证明:  ,我们可以设  ,  ,由于  因此    左右项拆开看,分别提取 n:   因此最终可得:  注:g(x)是复合函数,因此要对 (1-t) 再次求导,得到 - 1。 最大值(Maxium) ----------- 前面既然已经求出了导数,那么我们就可以求出伯恩斯坦多项式的峰值了,使导数的值等于 0 即可,我们来解一下:  即:    这个解释唯一的,因此**伯恩斯坦多项式会在 t = i/n 处有唯一的局部最大值**。 升阶(Degree raising)公式 -------------------- 升阶的意思,即把 n 阶的伯恩斯坦多项式写成 n+1 阶。即把它乘以 (1-t) 或者 t,如下: >  >  两者相加,即可得到: >  我们不能把  的二次多项式写成和  相关的三次多项式,除非 x=0,但是在伯恩斯坦多项式却可以。 积分(Integral) ------------ >  因此伯恩斯坦多项式的总面积并不是 1,曲线下的总面积为 1/(n+1),与 i 无关。 三角域的伯恩斯坦多项式 ----------- 这个在三角域贝塞尔曲面里非常的重要!!!!!! 什么叫三角域的伯恩斯坦多项式呢,我们还是拿开礼包的例子来说明,如下: 假如我有一个礼包,可以开到 A,B,C 三种物体中的一个,并且不存在一个都开不到的情况。其中开到 A 的概率为 u,开到 B 的概率为 v,开到 C 的概率为 w,且 u+v+w=1。那么我问如果我开这个礼包 n 次,开到 i 个 A,j 个 B,k 个 C 的概率是多少?因为必出,所以 i+j+k=n。 首先不考虑排列组合的情况,那么概率自然是  了,接着我们把组合数怎么算,首先我们要在 n 里面放 i 个,那么就会得到 (这个在前面解释过了,就不多说了),然后要在 n-i 个里放 j 个,那么就是 ,最后在 n-i-j 里放 k 个,那么就是 ,因为 n-i-j-k=0,三者相乘得到的就是 n! 。然后算重复的情况分别会有 i!,j!,k! 次重复,所以最终的概率为  。 那么我们就可以得到这样一个伯恩斯坦多项式: >  其中 u,v,w 不就是我们三角形的重心坐标的概念嘛,因此我们称之为三角域的伯恩斯坦多项式。 接着在问个问题,  有多少项?我们知道  中 i 的取值范围是 0 到 n ,因此  一共会有 n+1 项,那么对于三角域的伯恩斯坦多项式有多少项呢?我们应该怎么算。 这里我们可以这么想,当我 i=0 时,j 的取值范围可以是 0 到 n ,而当我 j 确定了,k 也就确定了,例如 j=1 那么 k 必须等于 n-1,否则不能保证 i+j+k=1。因此 i=0 时一共有 n+1 项,那么 i=1 时有多少项呢?显然是 n 项,因为 j 的取值范围变为 0 到 n-1 。那么我 i 可以从 0 到 n,对应的项从 n+1 慢慢递减,即可得到 (n+1)+n+(n-1)+...+1,其中一共 n+1 项,头尾相加乘以项数除以 2,即  一共有  项。 接下来再讲讲三角域的伯恩斯坦多项式的一些性质,大部分和正常的伯恩斯坦多项式没啥两样。 非负性 --- >  归一性 --- >  递归性 --- 递归性很重要,我们要用它来推导出 de Casteljau 算法。 我们用常理来理解,懒得写公式了,我们原本要开 n 个礼包,其中想要 i 个 A,j 个 B,k 个 C。但是现在我们发现,妈的钱不够,只买得起开 n-1 个礼包了,那么必然只能有下面三种情况: 情况 1: i-1 个 A,j 和 k 不变,那么概率应该是  情况 2: j-1 个 B,i 和 k 不变,那么概率应该是  情况 3: k-1 个 C,i 和 j 不变,那么概率应该是  这个时候,突然有个大佬说他送你一个礼包,那么如果: 1:在情况 1 后,你用送的礼包在 u 的概率下开出了 A,那种总概率就是  2:在情况 2 后,你用送的礼包在 v 的概率下开出了 B,那种总概率就是  3:在情况 3 后,你用送的礼包在 w 的概率下开出了 C,那种总概率就是  上面三种的结果不都又变成了你 n 个礼包开到了 i 个 A,j 个 B,k 个 C 么,因此: >  该公式就是我们的递归公式。 Unity的内存管理与性能优化 贝塞尔曲线与曲面(Bezier Curve and Surface)的详细介绍与代码实现