0710学习 agile Posted on Jul 10 2023 面试 leetcode学习 - 剑指 Offer 41. 数据流中的中位数 如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。 例如, [2,3,4] 的中位数是 3 [2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构: void addNum(int num) - 从数据流中添加一个整数到数据结构中。 double findMedian() - 返回目前所有元素的中位数。 ---  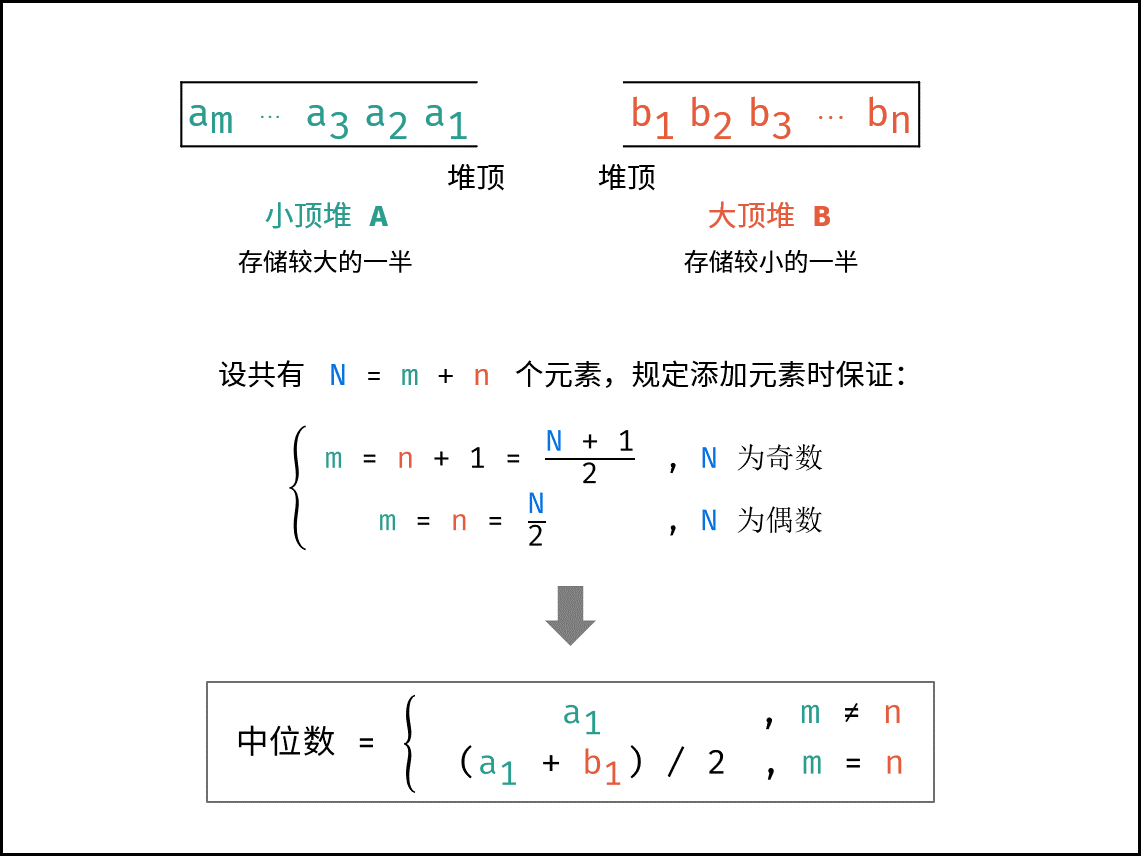 --- ```C# public class MedianFinder { private readonly List<int> _bigHeap; private readonly List<int> _smallHeap; private int _size = 0; /** initialize your data structure here. */ public MedianFinder() { _bigHeap = new List<int>(); _smallHeap = new List<int>(); } public void AddNum(int num) { //当前是__size是奇数 if (((_size + 1) & 1) == 0) { var bigValue = _bigHeap[0]; if (bigValue > num) { _bigHeap[0] = num; __Lower(_bigHeap, 0, __CompareBig); _smallHeap.Add(bigValue); } else { _smallHeap.Add(num); } __Grow(_smallHeap, _smallHeap.Count - 1, __CompareBig); } else { if (_size > 1) { var smallValue = _smallHeap[0]; if (num > smallValue) { _smallHeap[0] = num; var bigMaxValue = _bigHeap[0]; _bigHeap[0] = smallValue; _bigHeap.Add(bigMaxValue); __Lower(_smallHeap, 0, __CompareSmall); } else { _bigHeap.Add(num); } __Grow(_bigHeap, _bigHeap.Count - 1, __CompareSmall); } else { _bigHeap.Add(num); } } _size++; } public double FindMedian() { if (_size <= 0) { return 0; } //奇数 if (((_size + 1) & 1) == 0) { return _bigHeap[0]; } return (_smallHeap[0] + _bigHeap[0]) / 2.0f; } private bool __CompareBig(int i, int i1) { return i > i1; } private bool __CompareSmall(int i, int i1) { return i < i1; } private int __Parent(int i) { return (i - 1) >> 2; } private int __Left(int p) { return (p << 2) + 1; } private int __Right(int p) { return (p << 2) + 2; } private void __Lower(List<int> heap, int index, Func<int, int, bool> compare) { var length = heap.Count; while (true) { var compareIndex = index; var left = __Left(index); var right = __Right(index); if (left < length && compare(heap[left], heap[compareIndex])) { compareIndex = left; } if (right < length && compare(heap[right], heap[compareIndex])) { compareIndex = right; } if (compareIndex == index) { break; } (heap[compareIndex], heap[index]) = (heap[index], heap[compareIndex]); index = compareIndex; } } private void __Grow(List<int> heap, int index, Func<int, int, bool> compare) { int length = heap.Count; while (true) { var parent = __Parent(index); var compareIndex = parent; if (parent >= 0 && compare(heap[parent], heap[index])) { compareIndex = index; } if (compareIndex == parent) { break; } (heap[parent], heap[index]) = (heap[index], heap[parent]); index = parent; } } } ``` --- 通过优先级队列实现 ```C# public class MedianFinderBigCompare : IComparer<int> { public int Compare(int x, int y) { if (x == y) { return 0; } if (x > y) { return -1; } return 1; } } public class MedianFinderSys { private PriorityQueue<int, int> _priorityQueueSmall; private PriorityQueue<int, int> _priorityQueueBig; private int _size; public MedianFinderSys() { _priorityQueueBig = new PriorityQueue<int, int>(new MedianFinderBigCompare()); _priorityQueueSmall = new PriorityQueue<int, int>(); } public void AddNum(int num) { //当前是__size是奇数 if (((_size + 1) & 1) == 0) { var big = _priorityQueueBig.Peek(); if (big > num) { _priorityQueueBig.Dequeue(); _priorityQueueBig.Enqueue(num, num); _priorityQueueSmall.Enqueue(big, big); } else { _priorityQueueSmall.Enqueue(num, num); } } else { if (_size > 1) { var small = _priorityQueueSmall.Peek(); if (small < num) { _priorityQueueSmall.Dequeue(); _priorityQueueSmall.Enqueue(num, num); _priorityQueueBig.Enqueue(small, small); } else { _priorityQueueBig.Enqueue(num, num); } } else { _priorityQueueBig.Enqueue(num, num); } } _size++; } public double FindMedian() { if (_size <= 0) { return 0; } //奇数 if (((_size + 1) & 1) == 0) { return _priorityQueueBig.Peek(); } return (_priorityQueueBig.Peek() + _priorityQueueSmall.Peek()) / 2.0f; } } ``` - 剑指 Offer 55 - I. 二叉树的深度 输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。 --- ```C# public int MaxDepth(TreeNode root) { if (root == null) { return 0; } return 1 + Math.Max(MaxDepth(root.left), MaxDepth(root.right)); } public int MaxDepth2(TreeNode root) { if (root == null) { return 0; } var queue = new Queue<TreeNode>(); queue.Enqueue(root); var dep = 0; while (queue.Count > 0) { var size = queue.Count; for (int i = 0; i < size; i++) { var node = queue.Dequeue(); if (node.left != null) { queue.Enqueue(node.left); } if (node.right != null) { queue.Enqueue(node.right); } } dep++; } return dep; } ``` --- - 剑指 Offer 55 - II. 平衡二叉树 输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。 ---  --- ```C# public bool IsBalanced(TreeNode root) { if (root == null) { return true; } var left = __Dfs(root.left); var right = __Dfs(root.right); return Math.Abs(left - right) <= 1 && IsBalanced(root.left) && IsBalanced(root.right); } public int __Dfs(TreeNode root) { if (root == null) { return 0; } return 1 + Math.Max(__Dfs(root.left), __Dfs(root.right)); } public bool IsBalanced2(TreeNode root) { return __Help(root) != -1; } private int __Help(TreeNode root) { if (root == null) { return 0; } var left = __Help(root.left); if (left == -1) { return -1; } var right = __Help(root.right); if (right == -1) { return -1; } return Math.Abs(left - right) <= 1 ? Math.Max(left, right) + 1 : -1; } ``` --- - 剑指 Offer 64. 求 1 + 2 + … + n 求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。 ---  --- ```C# public int SumNums(int n) { _ = n > 1 && (n += SumNums(n - 1)) > 0; return n; } ``` --- - 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。” 说明: 所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。 ---  --- ```C# public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root == null) { return null; } if (p.val > root.val ^ q.val > root.val || root.val == p.val || root.val == q.val) { return root; } if (root.val > p.val && root.val > q.val) { return LowestCommonAncestor(root.left, p, q); } return LowestCommonAncestor(root.right, p, q); } public TreeNode LowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) { while (true) { if (root.val > p.val && root.val > q.val) { root = root.left; }else if (root.val < p.val && root.val < q.val) { root = root.right; } else { return root; } } } ``` --- - 剑指 Offer 68 - II. 二叉树的最近公共祖先 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。” 所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉树中。 --- 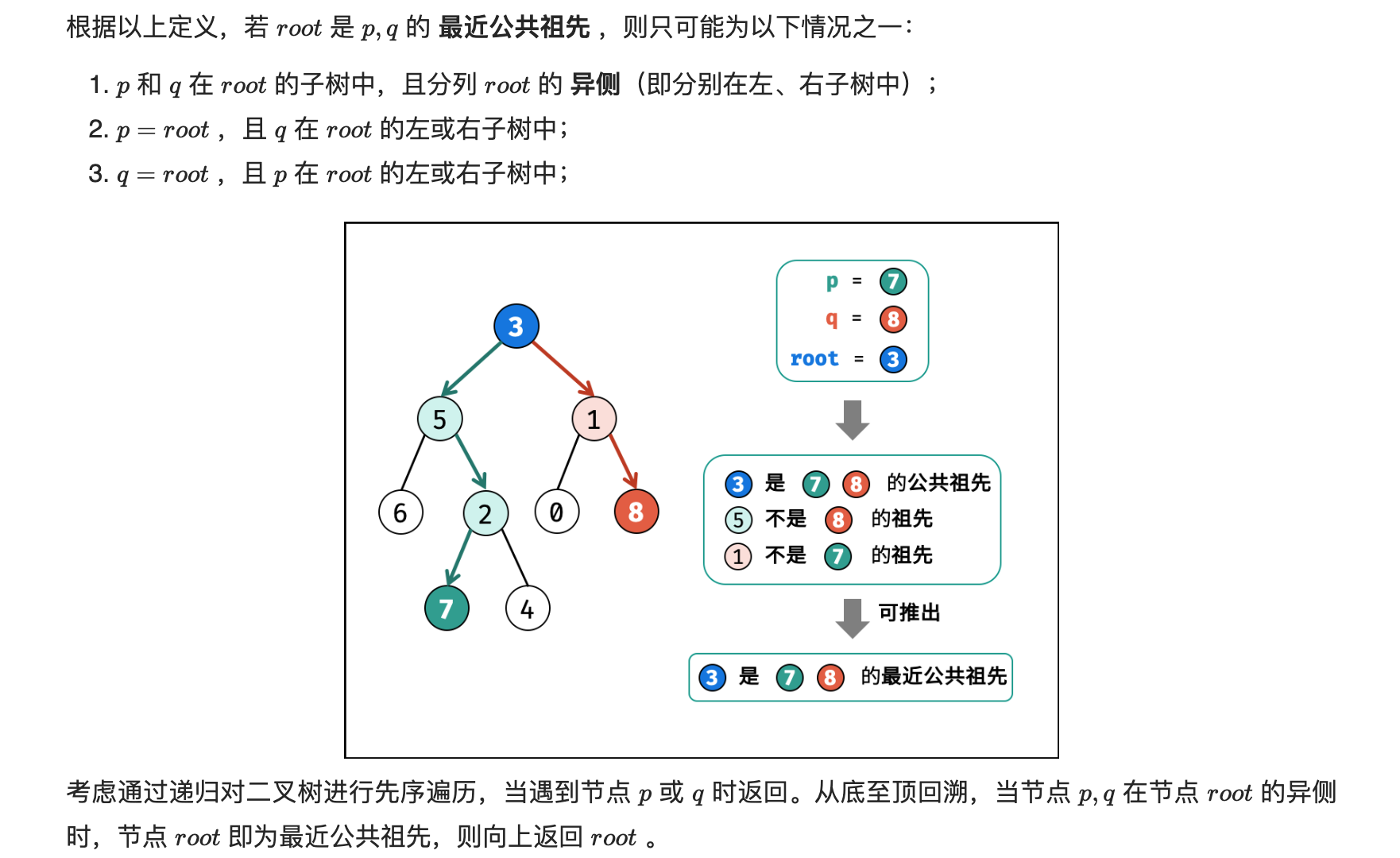  --- ```C# public TreeNode LowestCommonAncestor3(TreeNode root, TreeNode p, TreeNode q) { var nodeP = new List<TreeNode>(); var nodeQ = new List<TreeNode>(); __FindPath(root, p, nodeP); __FindPath(root, q, nodeQ); nodeP.AddRange(nodeQ); nodeQ.AddRange(nodeP); for (var i = 0; i < nodeP.Count; i++) { if (nodeP[i] == nodeQ[i]) { return nodeP[i]; } } return null; } private bool __FindPath(TreeNode node, TreeNode p, List<TreeNode> nodes) { if (node == null) { return false; } if (node.val == p.val) { nodes.Add(node); return true; } var flag = __FindPath(node.left, p, nodes) || __FindPath(node.right, p, nodes); if (flag) { nodes.Add(node); } return flag; } public TreeNode LowestCommonAncestor4(TreeNode root, TreeNode p, TreeNode q) { if (root == null || root.val == q.val || root.val == p.val) { return root; } var left = LowestCommonAncestor4(root.left, p, q); var right = LowestCommonAncestor4(root.right, p, q); if (left == null && right == null) //1 { return null; } if (left == null) //3 { return right; } if (right == null) //4 { return left; } return root; //2. if(left != null and right != null) } ``` 0711学习 0709学习