0804学习 agile Posted on Aug 4 2023 面试 二维 岛屿 深度优先搜索 数组 矩阵 图论 leetcode学习 - 图像渲染-733 有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。 你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行 上色填充 。 为了完成 上色工作 ,从初始像素开始,记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为 newColor 。 最后返回 经过上色渲染后的图像 。 示例 1: 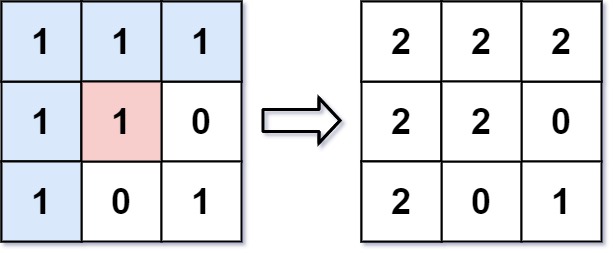 `输入: image = [[1,1,1],[1,1,0],[1,0,1]],sr = 1, sc = 1, newColor = 2 输出: [[2,2,2],[2,2,0],[2,0,1]] 解析: 在图像的正中间,(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。 注意,右下角的像素没有更改为2,因为它不是在上下左右四个方向上与初始点相连的像素点。` 示例 2: `输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2 输出: [[2,2,2],[2,2,2]]` 提示: m == image.length n == image[i].length 1 <= m, n <= 50 0 <= image[i][j], newColor < 216 0 <= sr < m 0 <= sc < n --- ```C# public int[][] FloodFill(int[][] image, int sr, int sc, int color) { var targetColor = image[sr][sc]; if (targetColor == color) { return image; } var row = image.Length; var column = image[0].Length; var stack = new Stack<int[]>(); stack.Push(new[] { sr, sc }); image[sr][sc] = color; int[] dx = { 1, 0, 0, -1 }; int[] dy = { 0, 1, -1, 0 }; while (stack.Count > 0) { var size = stack.Count; for (var i = 0; i < size; i++) { var tuple = stack.Pop(); var r = tuple[0]; var c = tuple[1]; for (int j = 0; j < 4; j++) { var nr = r + dx[j]; var nc = c + dy[j]; if (nr >= 0 && nr < row && nc >= 0 && nc < column && image[nr][nc] == targetColor) { image[nr][nc] = color; stack.Push(new[] { nr, nc }); } } } } return image; } ``` --- - 岛屿数量 给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。 此外,你可以假设该网格的四条边均被水包围。 示例 1: 输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1 示例 2: 输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3 提示: m == grid.length n == grid[i].length 1 <= m, n <= 300 grid[i][j] 的值为 '0' 或 '1' --- ```C# private int __row; private int __column; private int __num; private char[][] __grid; private int[] __dx; private int[] __dy; public int NumIslands(char[][] grid) { __grid = grid; __row = grid.Length; __column = grid[0].Length; __num = 0; __dx = new[] { 1, 0, 0, -1 }; __dy = new[] { 0, 1, -1, 0 }; for (var m = 0; m < __row; m++) { for (var n = 0; n < __column; n++) { var g = grid[m][n]; if (g != '1') continue; __num++; __Help(m, n); } } return __num; } private void __Help(int m, int n) { __grid[m][n] = '2'; for (var i = 0; i < 4; i++) { var nm = m + __dx[i]; var nn = n + __dy[i]; if (nm < __row && nm >= 0 && nn < __column && nn >= 0 && __grid[nm][nn] == '1') { __Help(nm, nn); } } } private int[] __dp; //并查集实现 public int NumIslands2(char[][] grid) { __grid = grid; __row = grid.Length; __column = grid[0].Length; __dp = new int[__row * __column]; for (var i = 0; i < __row; i++) { for (var j = 0; j < __column; j++) { var index = i * __column + j; __dp[index] = index; if (__grid[i][j] == '1') { __num++; } } } for (int i = 0; i < __row; i++) { for (int j = 0; j < __column; j++) { if (__grid[i][j] == '1') { if (i + 1 < __row && __grid[i + 1][j] == '1') { __Union(i * __column + j, (i + 1) * __column + j); } if (j + 1 < __column && __grid[i][j + 1] == '1') { __Union(i * __column + j, i * __column + j + 1); } } } } return __num; } private int __Find(int i) { var d = __dp[i]; return d == i ? i : __Find(d); } private void __Union(int i, int j) { var di = __Find(i); var dj = __Find(j); //避免重复合并操作 if (di == dj) { return; } __dp[di] = __dp[dj]; __num--; } ``` --- - 岛屿的周长-463 给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。 网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。 岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。 示例 1: 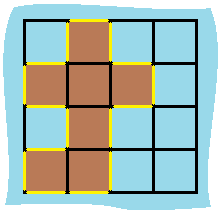 `输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] 输出:16 解释:它的周长是上面图片中的 16 个黄色的边` 提示: row == grid.length col == grid[i].length 1 <= row, col <= 100 grid[i][j] 为 0 或 1 --- ```C# private int[][] __grid; private int __num; private int __row; private int __column; private int[] __dx = { 1, 0, 0, -1 }; private int[] __dy = { 0, 1, -1, 0 }; public int IslandPerimeter(int[][] grid) { __num = 0; __row = grid.Length; __column = grid[0].Length; __grid = grid; for (int i = 0; i < __row; i++) { for (int j = 0; j < __column; j++) { if (grid[i][j] == 1) { __Help(i, j); } } } return __num; } private void __Help(int x, int y) { var length = 4; for (int i = 0; i < 4; i++) { var nx = x + __dx[i]; var ny = y + __dy[i]; if (nx >= 0 && nx < __row && ny >= 0 && ny < __column && __grid[nx][ny] == 1) { length--; } } __num += length; } public int IslandPerimeter2(int[][] grid) { __num = 0; __row = grid.Length; __column = grid[0].Length; __grid = grid; var edge = 0; for (int i = 0; i < __row; i++) { for (int j = 0; j < __column; j++) { if (grid[i][j] == 1) { __num++; if (i + 1 < __row && grid[i + 1][j] == 1) { edge += 1; } if (j + 1 < __column && grid[i][j + 1] == 1) { edge += 1; } } } } //总的周长,减去相邻边 return __num * 4 - edge * 2; } ``` --- - 被围绕的区域-130 给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。 示例 1: [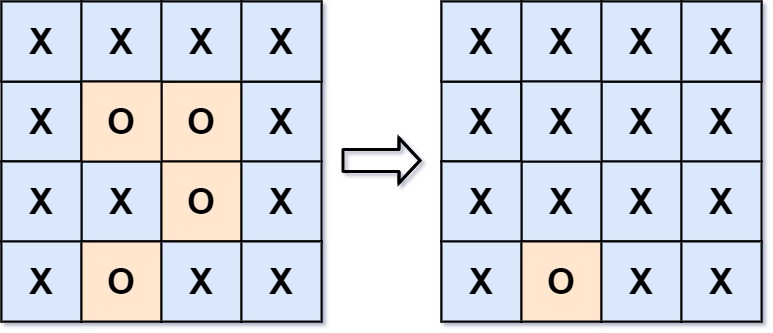](https://tools.nxcloud.club:12500/image/0KZv) `输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]] 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] 解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。` 提示: m == board.length n == board[i].length 1 <= m, n <= 200 board[i][j] 为 'X' 或 'O' --- ```C# private char[][] __board; private int __row; private int __column; private int[] __dx = { 1, 0, 0, -1 }; private int[] __dy = { 0, 1, -1, 0 }; private bool[][] __visited; //这样处理思路有问题,虽然答案正确 public void Solve(char[][] board) { __board = board; __row = board.Length; __column = board[0].Length; __visited = new bool[__row][]; for (int i = 0; i < __row; i++) { __visited[i] = new bool[__column]; } var cache = new List<int[]>(); for (var i = 1; i < __row - 1; i++) { for (var j = 1; j < __column - 1; j++) { if (__board[i][j] == 'O' && !__visited[i][j]) { __visited[i][j] = true; var flag = false; cache.Clear(); cache.Add(new int[] { i, j }); var lastSize = 0; while (cache.Count > lastSize) { var currentSize = cache.Count; for (var k = lastSize; k < currentSize; k++) { var x = cache[k][0]; var y = cache[k][1]; for (var l = 0; l < 4; l++) { var nx = x + __dx[l]; var ny = y + __dy[l]; if (nx >= 0 && ny >= 0 && nx < __row && ny < __column && __board[nx][ny] == 'O' && !__visited[nx][ny]) { if (nx == 0 || ny == 0 || nx == __row - 1 || ny == __column - 1) { flag = true; } cache.Add(new[] { nx, ny }); __visited[nx][ny] = true; } } } lastSize = currentSize; } if (!flag) { foreach (var t in cache) { var x = t[0]; var y = t[1]; __board[x][y] = 'X'; } } } } } } ``` --- 对于每一个边界上的 O,我们以它为起点,标记所有与它直接或间接相连的字母 O --- ```C# public void Solve2(char[][] board) { __board = board; __row = board.Length; __column = board[0].Length; for (var i = 0; i < __row; i++) { __HelpSet(i, 0); __HelpSet(i, __column - 1); } for (int i = 0; i < __column; i++) { __HelpSet(0, i); __HelpSet(__row - 1, i); } for (var i = 0; i < __row; i++) { for (var j = 0; j < __column; j++) { switch (__board[i][j]) { case 'O': __board[i][j] = 'X'; break; case 'o': __board[i][j] = 'O'; break; } } } } private void __HelpSet(int i, int j) { if (__board[i][j] == 'O') { __board[i][j] = 'o'; __Help(i, j); } } private void __Help(int i, int j) { for (int k = 0; k < 4; k++) { var x = i + __dx[k]; var y = j + __dy[k]; if (x >= 0 && y >= 0 && x < __row && y < __column && __board[x][y] == 'O') { __board[x][y] = 'o'; __Help(x, y); } } } ``` --- - 岛屿的最大面积-695 给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。 岛屿的面积是岛上值为 1 的单元格的数目。 计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。 示例 1: [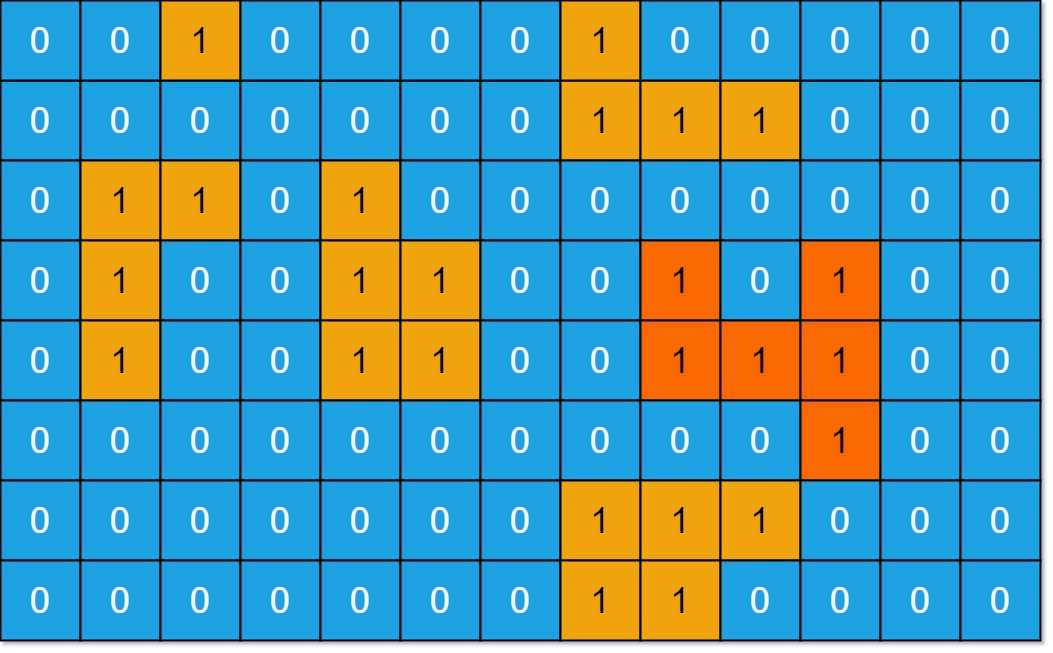](https://tools.nxcloud.club:12500/image/0UQ7) `输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。` 示例 2: `输入:grid = [[0,0,0,0,0,0,0,0]] 输出:0` 提示: m == grid.length n == grid[i].length 1 <= m, n <= 50 grid[i][j] 为 0 或 1 --- ```C# private int[][] __grid; private int __row; private int __column; private int __maxArea; private int[] __dx = { 1, 0, 0, -1 }; private int[] __dy = { 0, 1, -1, 0 }; public int MaxAreaOfIsland(int[][] grid) { __grid = grid; __row = grid.Length; __column = grid[0].Length; __maxArea = 0; for (int i = 0; i < __row; i++) { for (int j = 0; j < __column; j++) { if (__grid[i][j] == 1) { __grid[i][j] = 2; var area = 1; __Help(i, j, ref area); __maxArea = Math.Max(__maxArea, area); } } } return __maxArea; } private void __Help(int i, int j, ref int area) { for (int k = 0; k < 4; k++) { var x = i + __dx[k]; var y = j + __dy[k]; if (x >= 0 && y >= 0 && x < __row && y < __column && __grid[x][y] == 1) { __grid[x][y] = 2; area += 1; __Help(x, y, ref area); } } } ``` --- - 单词搜索-79 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。 示例 1:  `输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" 输出:true` 示例 2: `输入:board = [["A","B","C","E"],["S","F","E","S"],["A","D","E","E"]], word = "ABCESEEEFS" 输出:true` --- ```C# private char[][] __board; private string __word; private int __row; private int __column; private int[] __dx = { 1, -1, 0, 0 }; private int[] __dy = { 0, 0, 1, -1 }; private bool[][] __visited; public bool Exist(char[][] board, string word) { __board = board; __word = word; __row = __board.Length; __column = __board[0].Length; __visited = new bool[__row][]; for (int i = 0; i < __row; i++) { __visited[i] = new bool[__column]; } for (int i = 0; i < __row; i++) { for (var j = 0; j < __column; j++) { if (__Help(i, j, 0)) { return true; } } } return false; } private bool __Help(int i, int j, int index) { if (__board[i][j] != __word[index]) { return false; } if (index >= __word.Length - 1) { return true; } __visited[i][j] = true; for (var k = 0; k < 4; k++) { var x = i + __dx[k]; var y = j + __dy[k]; if (x >= 0 && y >= 0 && x < __row && y < __column && !__visited[x][y] && __board[x][y] == __word[index + 1]) { if (__Help(x, y, index + 1)) { return true; } } } //可能有重复字符,失败需要移除 __visited[i][j] = false; return false; } ``` --- - 课程表-207 你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。 例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。 请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。 示例 1: 输入:numCourses = 2, prerequisites = [[1,0]] 输出:true 解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。 提示: 1 <= numCourses <= 2000 0 <= prerequisites.length <= 5000 prerequisites[i].length == 2 0 <= ai, bi < numCourses prerequisites[i] 中的所有课程对 互不相同 --- **题意解释** - 一共有 n 门课要上,编号为 0 ~ n-1。 - 先决条件 [1, 0],意思是必须先上课 0,才能上课 1。 - 给你 n、和一个先决条件表,请你判断能否完成所有课程。 --- **再举个生活的例子** - 先穿内裤再穿裤子,先穿打底再穿外套,先穿衣服再戴帽子,是约定俗成的。 - 内裤外穿、光着身子戴帽子等,都会有点奇怪。 - 我们遵循穿衣的一条条先后规则,用一串 顺序行为,把衣服一件件穿上。 - 我们遵循课程之间的先后规则,找到一种上课顺序,把所有课一节节上完。 --- **用有向图描述依赖关系** - 示例:n = 6,先决条件表:[[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]] - 课 0, 1, 2 没有先修课,可以直接选。其余的课,都有两门先修课。 - 我们用有向图来展现这种依赖关系(做事情的先后关系):  - 这种叫 有向无环图,把一个 有向无环图 转成 线性的排序 就叫 拓扑排序。 - 有向图有 入度 和 出度 的概念: 如果存在一条有向边 A --> B,则这条边给 A 增加了 1 个出度,给 B 增加了 1 个入度。 - 所以,顶点 0、1、2 的入度为 0。顶点 3、4、5 的入度为 2。 --- **每次只能选你能上的课** - 每次只能选入度为 0 的课,因为它不依赖别的课,是当下你能上的课。 - 假设选了 0,课 3 的先修课少了一门,入度由 2 变 1。 - 接着选 1,导致课 3 的入度变 0,课 4 的入度由 2 变 1。 - 接着选 2,导致课 4 的入度变 0。 - 现在,课 3 和课 4 的入度为 0。继续选入度为 0 的课……直到选不到入度为 0 的课。 --- **这很像 BFS** - 让入度为 0 的课入列,它们是能直接选的课。 - 然后逐个出列,出列代表着课被选,需要减小相关课的入度。 - 如果相关课的入度新变为 0,安排它入列、再出列……直到没有入度为 0 的课可入列。 --- **总结:拓扑排序问题** - 根据依赖关系,构建邻接表、入度数组。 - 选取入度为 0 的数据,根据邻接表,减小依赖它的数据的入度。 - 找出入度变为 0 的数据,重复第 2 步。 - 直至所有数据的入度为 0,得到排序,如果还有数据的入度不为 0,说明图中存在环。 --- ```C# private Dictionary<int, List<int>> __adj; private int[] __vertex; public bool CanFinish(int numCourses, int[][] prerequisites) { __vertex = new int[numCourses]; __adj = new Dictionary<int, List<int>>(); foreach (var t in prerequisites) { var f = t[0]; var s = t[1]; __vertex[f]++; //记录入度值,也就是当前课程需要多少前置课程 if (__adj.TryGetValue(s, out var list)) { list.Add(f); } else { //记录有多少课程依赖他 __adj[s] = new List<int>() { f }; } } var queue = new Queue<int>(); for (var i = 0; i < numCourses; i++) { if (__vertex[i] == 0)// 值为0的课程表示可以直接上,没有前置课程 { queue.Enqueue(i); } } while (queue.Count > 0) { var pre = queue.Dequeue(); //出栈表示上完一门课 numCourses--; //总课程数减一 //获取依赖当前课程的课程列表,将他们的课程依赖数量减1 if (__adj.TryGetValue(pre, out var list)) { foreach (var cur in list) { //表示当前课程的依赖课程都上完了, //当前课程也可以上了,加入上课队列 if (--__vertex[cur] == 0) { queue.Enqueue(cur); } } } } return numCourses == 0; } ``` - 课程表 II-210 现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。 返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。 示例 2: 输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]] 输出:[0,2,1,3] 解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。 因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。 --- ```C# public int[] FindOrder(int numCourses, int[][] prerequisites) { int[] degrees = new int[numCourses]; var cache = new Dictionary<int, List<int>>(); var result = new List<int>(); var queue = new Queue<int>(); foreach (var t in prerequisites) { degrees[t[0]]++; //当前课程[t[0]]依赖数量+1,也就是入度+1 //更新t[1]课程依赖该课程列表 if (cache.TryGetValue(t[1], out var list)) { list.Add(t[0]); } else { cache[t[1]] = new List<int>() { t[0] }; } } for (int i = 0; i < numCourses; i++) { if (degrees[i] == 0) { queue.Enqueue(i); } } while (queue.Count > 0) { var c = queue.Dequeue(); result.Add(c); numCourses--; if (cache.TryGetValue(c, out var list)) { for (var i = 0; i < list.Count; i++) { if (--degrees[list[i]] == 0) { queue.Enqueue(list[i]); } } } } if (numCourses != 0) { result.Clear(); } return result.ToArray(); } ``` - 最小高度树 树是一个无向图,其中任何两个顶点只通过一条路径连接。 换句话说,一个任何没有简单环路的连通图都是一棵树。 给你一棵包含 n 个节点的树,标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表(每一个边都是一对标签),其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。 可选择树中任何一个节点作为根。当选择节点 x 作为根节点时,设结果树的高度为 h 。在所有可能的树中,具有最小高度的树(即,min(h))被称为 最小高度树 。 请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。 树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。 --- 示例 1:  `输入:n = 4, edges = [[1,0],[1,2],[1,3]] 输出:[1] 解释:如图所示,当根是标签为 1 的节点时,树的高度是 1 ,这是唯一的最小高度树。` 示例 2:  `输入:n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] 输出:[3,4]` 提示: 1 <= n <= 2 * 104 edges.length == n - 1 0 <= ai, bi < n ai != bi 所有 (ai, bi) 互不相同 给定的输入 保证 是一棵树,并且 不会有重复的边 --- ```C# private List<int> __result; private int[] __degree; public IList<int> FindMinHeightTrees(int n, int[][] edges) { __result = new List<int>(); if (edges.Length == 0) { __result.Add(0); return __result; } __degree = new int[n]; var cache = new Dictionary<int, List<int>>(); foreach (var edge in edges) { __degree[edge[0]]++; __degree[edge[1]]++; __AddCache(cache, edge[0], edge[1]); __AddCache(cache, edge[1], edge[0]); } var queue = new Queue<int>(); for (var i = 0; i < n; i++) { if (__degree[i] == 1) { queue.Enqueue(i); } } while (queue.Count > 0) { var count = queue.Count; __result.Clear(); //可以理解成每一轮移除度为1的值,最后result中留下的就是为最终结果,也就是仅剩下度为1的值 for (int i = 0; i < count; i++) { var v = queue.Dequeue(); __result.Add(v); if (cache.TryGetValue(v, out var neighbors)) { foreach (var neighbor in neighbors) { if (--__degree[neighbor] == 1) { queue.Enqueue(neighbor); } } } } } return __result; } private void __AddCache(Dictionary<int, List<int>> cache, int f, int s) { if (cache.TryGetValue(f, out var list)) { list.Add(s); } else { cache[f] = new List<int>() { s }; } } ``` 0816学习 0803学习