0825学习 agile Posted on Aug 25 2023 面试 unity基础 ## unity3d中ScriptingBackend选择mono和il2cpp的区别 **Mono介绍** --- Mono是一个开源的、跨平台的开发平台,允许开发者使用C#等编程语言来创建应用程序,这些应用程序可以在多个操作系统上运行,如Linux、macOS和Windows --- Mono主要组成包括`Mono编译器`,`Mono虚拟机`,`一个与.NET Framework相似的类库`。 1. Mono编译器将C#代码编译成一种称为中间语言(Intermediate Language,IL)的中间代码。 2. 在Mono运行时,Mono虚拟机(VM)会并将中间语言(IL)代码翻译成机器码在计算机上运行,从而实现跨平台 --- CIL或IL是.NET平台上的一种中间代码,是一种类似汇编语言的语法,用于表示高级编程语言的功能,但比机器码更抽象,更接近高级语言 --- 1. `JIT`:将IL代码转为对应平台机器码并且将机器码映射到虚拟内存中执行。JIT编译的时候IL是在依托Mono运行时,转为对应的机器码后再依托本地运行。 2. `AOT`:一种将源代码在应用程序部署之前编译成机器码的编译技术.在AOT编译中,代码在运行之前被完全编译成机器码,而不是在运行时逐行地解释和编译 3. `FAOT`:一种将整个应用程序在部署之前完全编译成机器码的方法。与传统的AOT编译不同,FAOT编译不仅仅是将核心代码编译为机器码,还包括应用程序的所有部分,例如库、模块和依赖项。 --- IOS并非把JIT禁止了。或者换个句式讲,IOS封了内存的可执行权限,相当于变相的封锁了JIT这种编译方式。 --- **优缺点** --- 1. 构建应用非常快 2. 支持运行时代码执行 3. Mono VM在各个平台移植异常麻烦,有几个平台就得移植几个VM(WebGL和UWP这两个平台只支持 IL2CPP) 4. Mono版本授权受限,C#很多新特性无法使用,Unity 2018 mono版本仍然是mono2.0、unity2020的版本更新到了mono 5.11 5. 对于Mono堆内存来说,由于Mono自身的限制,其堆内存分配是 “只升不降” 的,即内存一旦分配给Mono,不论以后该内存是否继续被使用,都不会再归还给系统。因此,建议您对于代码的堆内存分配进行严格的控制,避免不必要的Mono堆内存分配 6. iOS仍然支持Mono,但是不再允许Mono(32位)应用提交到Apple Store 7. 用mono打包的unity游戏,如果没有加密,可以通过 `assembly-csharp.dll`文件反编译看到源代码 8. 用il2cpp打包的unity游戏可以通过用`IL2CppDumper`运行 `libil2cpp.so` 和 `global-metadata.dat`来模拟取得 dll,但是这个 dll 只有函数名和偏移地址 --- **IL2CPP(AOT编译)** --- IL2CPP分为两个独立的部分: 1. `AOT(静态编译)编译器`:把IL中间语言转换成CPP文件 2. `il2cpp vm`:通过IL2CPP以后代码变成了静态的C++,但是内存管理这块还是遵循C#的方式,这也是为什么最后还要有一个 IL2CPPVM的原因:它负责提供诸如GC管理,线程创建这类的服务性工作 --- **编译区别** --- 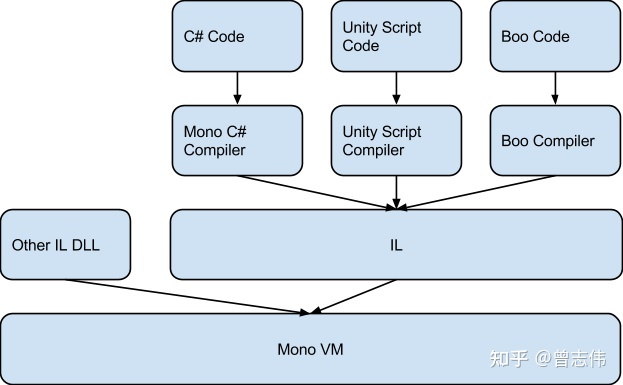 --- 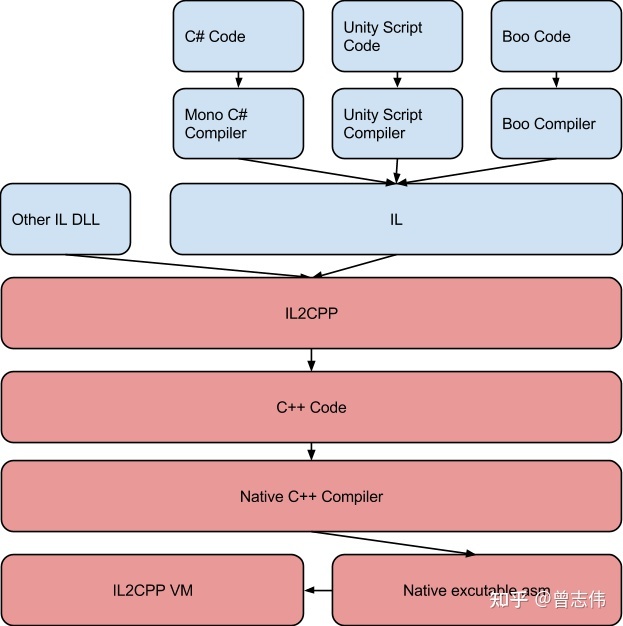 --- **IL2Cpp优缺点** --- 1. 运行效率快,根据官方的实验数据,换成IL2CPP以后,程序的运行效率有了1.5-2.0倍的提升 2. 利用现成的在各个平台的C++编译器对代码执行编译期优化,这样可以进一步减小最终游戏的尺寸并提高游戏运行速度。 3. 可以调试生成的C++代码 4. 可以启用引擎代码剥离(Engine code stripping)来减少代码的大小 5. 多平台移植非常方便 6. 相比Mono构建应用慢 7. 只支持AOT(Ahead of Time)编译 --- ##LUA为什么可以热更 --- LUA`解释型语言`,并不需要事先编译,而是运行时动态解释执行的。那C#为什么不做成解释型语言呢?因为C#的定位是一个追求效率且功能强大的编译型语言。这样LUA就和普通的游戏资源如图片,文本没有区别,因此可以在运行时直接从WEB服务器上下载到持久化目录并被其它LUA文件调用 --- ##Reserved Total 和 Used Total之间的关系 --- `Reserved Total`:当前项目所占据的总物理内存 `Used Total`:当前项目所使用的总物理内存 引擎在分配内存时并不是向操作系统 “即拿即用”,而是首先获取一定量的连续内存,然后供自己内部使用,待空余内存不够时,引擎才会向系统再次申请一定量的连续内存进行使用 `Reserved Total` 的内存占用量略大于 `Used Total`, 且两者走势基本一致 --- ##GetKey、GetButton,GetAxis及Input Manager --- - `GetKey`,`GetKeyDown`,`GetKeyUp`可以通过传入String类型的按键名称或KeyCode --- - 普通键:“a”,“b”,“c”...... - 数字键:“1”,“2”,“3”,...... - 箭头键:“up”, “down”, “left”, “right” - 键盘键:“[1]”, “[2]”, “[3]”, “[+]”, “[equals]” - 修改键:“right shift”, “left shift”, “right ctrl”, “left ctrl”, “right alt”, “left alt”, “right cmd”, “left cmd” - 鼠标按钮:“mouse 0”, “mouse 1”, “mouse 2”, … - 操纵杆按钮(来自任意操纵杆):“joystick button 0”, “joystick button 1”, “joystick button 2”, … - 操纵杆按钮(来自特定操纵杆):“joystick 1 button 0”, “joystick 1 button 1”, “joystick 2 button 0”, … - 特殊键: “backspace”, “tab”, “return”, “escape”, “space”, “delete”, “enter”, “insert”, “home”, “end”, “page up”, “page down” - 功能键:“f1”,“f2”,“f3”,... --- GetKey会当按键被按住时持续返回true值,GetKeyDown在按键按下瞬间返回true,GetKeyUp则在按键松开时返回true --- - GetButton、GetButtonDown、GetButtonUp、GetAxis、GetAxisRaw传入参数只能为InputManager中定义的轴键 --- 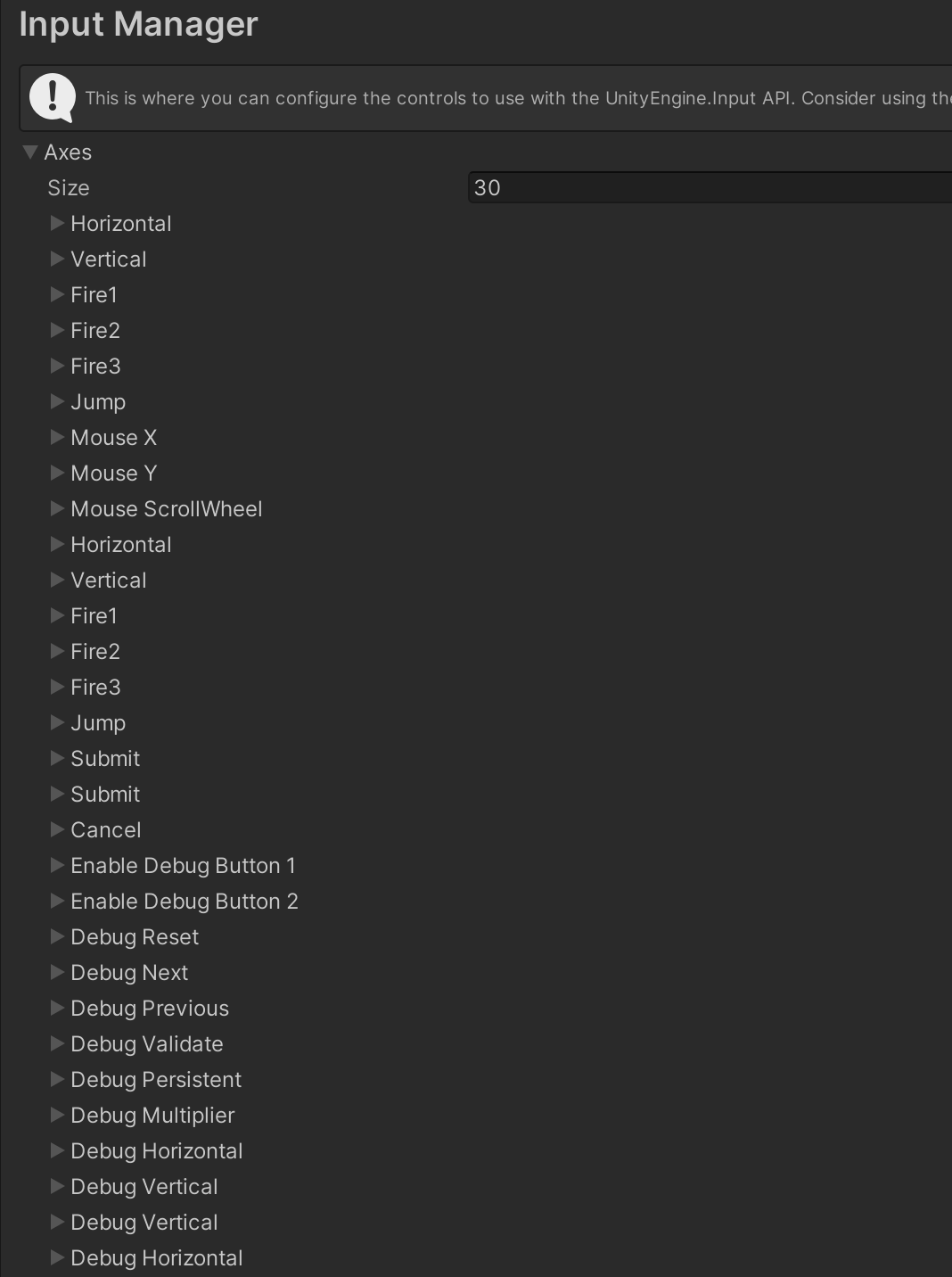 --- - Horizontal和Vertical映射到w,a,s,d和箭头键 - Fire1,Fire2,Fire3分别映射到Control,Option(Alt)和Command。 - Mouse X鼠标沿着屏幕X移动时触发 - Mouse Y鼠标沿着屏幕Y移动时触发 - GetAxis从0变到+1或-1,每一步增加/减少0.05f - GetAxisRaw立即从0更改为1或-1。 --- ##齐次坐标 齐次坐标就是将原本n维的向量用n+1维来表示,是用于投影几何里的坐标系统。可以这样理解,在Unity中有透视与正交两种相机模式,笛卡尔坐标系是用于正交模式空间下,而齐次坐标系是用于透视模式空间下 --- 齐次坐标的表示是计算机图形学中的重要手段之一,在笛卡尔坐标下无法区分是一个点还是一个向量,而在齐次坐标下可以明确区分点和向量 --- 当n+1维的值为0时,表示一个无穷远的点(例如一条平行的火车道,一直向远处看则会相交),齐次坐标在编写Shader时可能需要用到它 --- 引入齐次坐标的作用,把各种变换都统一了起来,即 把缩放,旋转,平移等变换都统一起来,都表示成一连串的矩阵相乘的形式。保证了形式上的线性一致性。 --- 如果把一个点从普通坐标变成齐次坐标,给x,y,z乘上同一个非零数w,然后增加第4个分量w;如果把一个齐次坐标转换成普通坐标,把前三个坐标同时除以第4个坐标,然后去掉第4个分量。 ---  点的齐次坐标可以表示为(x,y,z,1),向量的齐次坐标可以表示为(x,y,z,0) --- 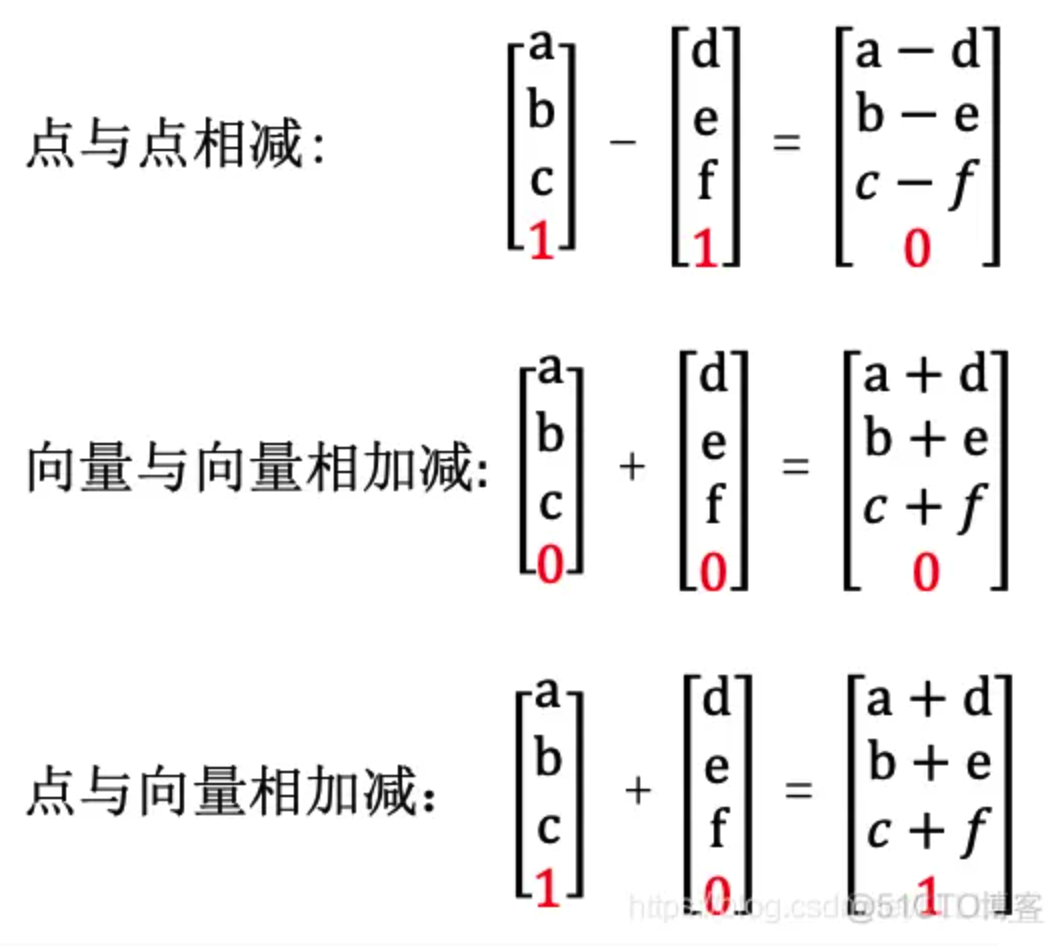 --- ##仿射变换 --- 仿射变换=线性变换+平移 --- 因为线性变换需要满足以下三个条件: - 变换前是直线的,变换后依然是直线 - 直线比例保持不变 - 变换前是原点的,变换后依然是原点 `缩放,旋转`操作都满足上面三个条件,但是`平移`操作`不满足变换前是原点的,变换后依然是原点`这个条件,所以不属于仿射变换 --- 最后得出结论仿射变换的条件有两个,一是变换前是直线的,变换后依然是直线,二是直线比例保持不变 --- ##变换矩阵模板 --- 因为平移操作不满足线性变换的条件,所以每个矩阵添加了一列去表示平移(tx/ty/tz分别代表在x/y/z轴上的平移的距离),前面的列表示缩放和旋转,因为3D游戏中一般才会进行矩阵计算,所以Unity中的矩阵都是4*4的  --- ##平移变换 --- tx代表在x轴上的移动距离,ty代表在y轴上的移动距离,tz代表在z轴上的移动距离  计算一个点p(x,y)或p(x,y,z)经过平移后的点。其实就是一个点移动一个向量的距离,可以理解为一个点与一个向量的加法  --- ##平移矩阵的逆矩阵 ---  --- ##缩放变换 --- sx代表在x轴上的缩放比例,sy代表在y轴上的缩放比例,sz代表在z轴上的缩放比例  计算一个点p(x,y)或p(x,y,z)经过缩放后的点。可以理解为一个点与不同轴上的缩放系数的乘法  --- ##缩放矩阵的逆矩阵 ---  --- ##旋转变换 --- θ代表旋转的角度  --- ##旋转矩阵的逆矩阵 ---  --- ##世界坐标转成本地坐标 --- ```C# public Vector3 ConvertToLocalPosition1(Vector3 worldPos) { var matrix = transform.worldToLocalMatrix; return matrix.MultiplyPoint(worldPos); } public Vector3 ConvertToLocalPosition2(Vector3 worldPos) { var matrix = transform.worldToLocalMatrix; return matrix.MultiplyPoint3x4(worldPos); } public Vector3 ConvertToLocalPosition3(Vector3 worldPos) { return transform.InverseTransformPoint(worldPos); } //注意这里如果是坐标一定要转成vector4 w为1 public Vector3 ConvertToLocalPosition4(Vector3 worldPos) { Vector4 v = worldPos; v.w = 1; return transform.worldToLocalMatrix * v; } ``` --- ##MultiplyPoint方法和MultiplyPoint3x4方法区别 --- ``` public Vector3 MultiplyPoint(Vector3 v) { Vector3 vector3; vector3.x = ( m00 * v.x + m01 * v.y + m02 * v.z) + m03; vector3.y = ( m10 * v.x + m11 * v.y + m12 * v.z) + m13; vector3.z = ( m20 * v.x + m21 * v.y + m22 * v.z) + m23; float num = 1f / ( ( m30 * v.x + m31 * v.y + m32 * v.z) + m33); // this is 1/1=1 when m30, m31, m32 = 0 and m33 = 1 vector3.x *= num; // so then multiplying by 1 is pointless.. vector3.y *= num; vector3.z *= num; return vector3; } ``` 可以看出multiplyPoint是通过w缩放之后的值。可以参考如下4x4 * 4x1 矩阵乘法  ---- ```C# public Vector3 MultiplyPoint3x4(Vector3 v) { Vector3 vector3; vector3.x = ( m00 * v.x + m01 * v.y + m02 * v.z) + m03; vector3.y = ( m10 * v.x + m11 * v.y + m12 * v.z) + m13; vector3.z = ( m20 * v.x + m21 * v.y + m22 * v.z) + m23; return vector3; } ``` 对于MultiplyPoint3x4方法,没有乘以w值,也就是默认w为1 [](https://tools.nxcloud.club:12500/image/8u8E) --- 从上面我们可以看出来,如果事先知道矩阵默认w为(0,0,0,1),还是用MultiplyPoint3x4方法效率高,在投影矩阵中必须用MultiplyPoint方法,因为投影矩阵w为(0,0,-1,0)  --- ##Matrix4x4.TRS --- Unity中的Matrix4x4类采用的是列矩阵,常规做法是把矢量放在矩阵的右侧,我们的阅读顺序是从右到左。 --- ```C# // Matrix4x4 使用Vector4 做为参数的构造方法 // 每一个Vector4参数都代表矩阵的一列 // 如 new Matrix4x4( // new Vector4(1,2,3,4), // new Vector4(5,6,7,8), // new Vector4(9,10,11,12), // new Vector4(13,14,15,16) // ); // 将会得到这样一个矩阵: // 1 5 9 13 // 2 6 10 14 // 3 7 11 15 // 4 8 12 16 public Matrix4x4(Vector4 column0, Vector4 column1, Vector4 column2, Vector4 column3) { this.m00 = column0.x; this.m01 = column1.x; this.m02 = column2.x; this.m03 = column3.x; this.m10 = column0.y; this.m11 = column1.y; this.m12 = column2.y; this.m13 = column3.y; this.m20 = column0.z; this.m21 = column1.z; this.m22 = column2.z; this.m23 = column3.z; this.m30 = column0.w; this.m31 = column1.w; this.m32 = column2.w; this.m33 = column3.w; } ``` --- 物体到父物体空间的变换矩阵(TRS) M = T * R * S,我们的变换顺序为先缩放,再旋转,最后平移(从右到左) --- `Matrix4x4.Translate(centerPos.position)`基于单位矩阵进行变化,位置信息会被记录在4x4矩阵的m03、m13、m23位置,在Unity中可以通过Matrix4x4.Translate()打印出位置矩阵。 Translate的矩阵表示为:  --- `Matrix4x4.Rotate(centerPos.rotation)`:旋转矩阵本身需要3x3矩阵,该矩阵记录了对象本地坐标的三个坐标轴的单位向量,即centerPos.Right和centerPos.Up以及centerPos.Forward三个坐标轴的向量。 矩阵数值与对象的局部坐标轴的单位向量相互对应,即对象的旋转矩阵表示为:  其中`R对应Right,而U对应Up,F则对应着Forward`,代表Unity本地坐标轴的三个分量 --- `Matrix4x4.Scale(centerPos.lossyScale)`:缩放矩阵  --- 通过矩阵的乘法来计算得到最后的矩阵,乘法的公式构成即Translate、Roate、Scale三个对应的基本转换矩阵,示例如下:  --- 经过矩阵的乘法运算得到结果就是对象的TRS矩阵,其具体结构为:  通过计算过程与结果来看,`Unity中的TRS矩阵是以列为主导的,前三行的前三列分别代表对象的坐标轴的单位向量与各个方向缩放的乘积,而剩下第四行用来表示位置信息` --- ```C# // transform.localToWorldMatrix 等价于Matrix4x4.TRS,等价于Matrix4x4.Translate*Matrix4x4.Rotate*Matrix4x4.Scale var m1 = Matrix4x4.TRS(transform.position, transform.rotation, transform.lossyScale); var m2 = Matrix4x4.Translate(transform.position) * Matrix4x4.Rotate(transform.rotation) * Matrix4x4.Scale(transform.lossyScale); ``` --- ##localToWorldMatrix其他推导方式 --- 如果有这样一个Transform层级: - A (父对象) - - B (子对象) - - - C (子孙对象) A的变换矩阵为`Ma`,可以将`A下的模型坐标转换到世界坐标`。 B的变换矩阵为`Mb`,可以将`B下的模型坐标转换到A的模型坐标`,进而`依靠A的变换矩阵`转换到世界坐标。 C的变换矩阵为`Mc`,可以将`C下的模型坐标转换到B的模型坐标`,然后再转换到`A的模型坐标`,再`转换到世界坐标`。 C的`localToWorldMatrix = Ma * Mb * Mc`(一定要确保变换顺序,从右至左) --- 模型坐标到父物体模型坐标的矩阵计算 ```C# //GetChildToParentMatrix(__target) * localPos 可以算出子节点的localpos,在父节点下的localpos的大小 private Matrix4x4 GetChildToParentMatrix(Transform trans) { var matrixT = Matrix4x4.Translate(trans.localPosition); var matrixS = Matrix4x4.Scale(trans.localScale); var matrixRz = new Matrix4x4( new Vector4(Mathf.Cos(trans.localEulerAngles.z * Mathf.Deg2Rad), Mathf.Sin(trans.localEulerAngles.z * Mathf.Deg2Rad), 0, 0), new Vector4(-Mathf.Sin(trans.localEulerAngles.z * Mathf.Deg2Rad), Mathf.Cos(trans.localEulerAngles.z * Mathf.Deg2Rad), 0, 0), new Vector4(0, 0, 1, 0), new Vector4(0, 0, 0, 1)); var matrixRx = new Matrix4x4(new Vector4(1, 0, 0, 0), new Vector4(0, Mathf.Cos(trans.localEulerAngles.x * Mathf.Deg2Rad), Mathf.Sin(trans.localEulerAngles.x * Mathf.Deg2Rad), 0), new Vector4(0, -Mathf.Sin(trans.localEulerAngles.x * Mathf.Deg2Rad), Mathf.Cos(trans.localEulerAngles.x * Mathf.Deg2Rad), 0), new Vector4(0, 0, 0, 1)); var matrixRy = new Matrix4x4( new Vector4(Mathf.Cos(trans.localEulerAngles.y * Mathf.Deg2Rad), 0, -Mathf.Sin(trans.localEulerAngles.y * Mathf.Deg2Rad), 0), new Vector4(0, 1, 0, 0), new Vector4(Mathf.Sin(trans.localEulerAngles.y * Mathf.Deg2Rad), 0, Mathf.Cos(trans.localEulerAngles.y * Mathf.Deg2Rad), 0), new Vector4(0, 0, 0, 1)); // var matrixR = Matrix4x4.Rotate(trans.localRotation); // 旋转矩阵乘法按照Y * X * Z -> 先旋转的放在最后 var matrixR = matrixRy * matrixRx * matrixRz; return matrixT * matrixR * matrixS; } ``` --- ##观察空间 --- 观察空间(view space)也被称为摄像机空间(camera space)。观察空间可以认为是模型空间(model space)的特例,特殊的模型也就是摄像机。 --- unity在模型空间和世界空间中选用的是左手坐标系,而在观察空间中选用的是右手坐标系。这符合opengl的传统,这也就解释了摄像机的正前方指向的是-z轴方向 --- 观察空间是一个3d空间,屏幕空间是一个二维空间,从观察空间转到屏幕空间的转换需要经过一个操作,那就是投影。 --- 从世界空间变换到观察空间的转换叫做观察变换(view transform)。 --- ```C# //m1,m2,m3等价,可以把camera当做普通物体,那从普通物体坐标系转换成世界坐标系可以通过Matrix4x4.TRS来实现 //但camera有点特殊,首先是缩放对他没有什么作用,他就是单纯的坐标系,所以得去掉缩放矩阵大影响,这里可以直接传如缩放大小Vector3.one //当然也可以传入Camera.main.transform.lossyScale实际缩放大小,最后乘以下Matrix4x4.Scale(Camera.main.transform.lossyScale).inverse,来去掉scale的影响 //其次camera的本地坐标系是右手坐标系,z轴的方向正好跟左手坐标系相反。因此得对z分量取反操作,这里通过乘以Matrix4x4.Scale(new Vector3(1, 1, -1)来实现 var m1 = Camera.main.cameraToWorldMatrix; var m2 = Matrix4x4.TRS(Camera.main.transform.position, Camera.main.transform.rotation, Vector3.one) * Matrix4x4.Scale(new Vector3(1, 1, -1)); var m3 = Matrix4x4.TRS(Camera.main.transform.position, Camera.main.transform.rotation, Camera.main.transform.lossyScale) * Matrix4x4.Scale(Camera.main.transform.lossyScale).inverse * Matrix4x4.Scale(new Vector3(1, 1, -1)); ``` ---  --- ##worldToLocalMatrix(世界转局部的转换矩阵) --- 旋转矩阵的逆矩阵等于旋转矩阵的转置矩阵 ``` Matrix4x4.Rotate(__target.localRotation).transpose; Matrix4x4.Rotate(__target.localRotation).inverse; ```  --- 位置矩阵的反矩阵: `Matrix4x4.Translate(centerPos.position).inverse`  --- 缩放的逆矩阵: `Matrix4x4.Scale(centerPos.localScale).inverse`  --- 矩阵的乘法,我们当然也可以得到最后的计算结果: 得到Translate、Rotate、Scale的变换矩阵后,就可以对其执行乘法操作,但是与TRS不同的是,该矩阵的顺序为`SRT`,代码为: `Matrix4x4.Scale(centerPos.localScale).inverse * Matrix4x4.Rotate(centerPos.rotation).transpose * Matrix4x4.Translate(centerPos.position).inverse;`  --- ##快捷键小提示 快捷键F、Shift+F、Ctrl+Shift+F: 选择游戏对象,按下F键,可将Scene的视口中央移动到该游戏对象处;按下Shift+F,可将视口与该游戏对象锁定,即无论如何移动游戏对象,视口中央始终跟随此游戏对象。在Hierarchy面板中选择摄像机,按下Ctrl+Shift+F,可将摄像机移动到能够呈现Scene窗口中内容的位置。 git命令02 0620学习