0928学习 agile Posted on Sep 28 2023 面试 navmesh ### 深度优先搜索算法(DFS) 是一种用于`遍历或搜索树或图`的算法。沿着`树的深度遍历树的节点`,尽可能`深的搜索树`的分支,以`栈`来实现算法 --- ### 广度优先搜索(BFS) 一种`盲目搜寻法`,目的是系统地展开并检查图中的所有节点,以找寻结果 --- ####步骤 --- - 首先将根节点放入队列中。 - 从队列中取出第一个节点,并检验它是否为目标。 - 如果找到目标,则结束搜寻并回传结果。 - 否则将它所有尚未检验过的直接子节点(邻节点)加入队列中。 - 若队列为空,表示整张图都检查过了。结束搜寻并回传“找不到目标” --- ```C# var frontier = new Array(); frontier.put(start); var visited = new Array(); visited[start] = true; while(frontier.length>0){ current = frontier.get(); //查找周围顶点 for(next in graph.neighbors(current)) { var notInVisited = visited.indexOf(next)==-1; //没有访问过 if(notInVisited) { frontier.put(next); visited[next] = true; } } } ``` --- ####缺点 - 效率底下, 时间复杂度是:`T(n) = O(n^2)` - 每个顶点之间没有权值,无法定义优先级,不能找到最优路线。遇到水域需要绕过行走,他会直接穿过障碍物,这不是我们想要的结果 --- ###Dijkstra 算法 --- - 基于BFS进行改进,为每个顶点之间的边增加一个权值 - 利用贪心算法计算并最终能够产生最优结果 - 优先队列采用的是,每个顶点到起始顶点的预估值来进行排序 ####步骤 --- - 每个顶点都包含一个预估值`cost`(起点到当前顶点的距离),每条边都有权值`v` ,初始时,只有起始顶点的预估值`cost`为`0`,其他顶点的预估值d都为无穷大`∞`。 - 查找`cost`值最小的顶点A,放入`openPath`队列 - 循环A的直接子顶点,获取子顶点当前`cost`值命名为`current_cost`,并计算新路径`new_cost`,`new_cost=父节点A的cost+v(父节点到当前节点的边权值)`,如果`new_cost<current_cost`,当前顶点的`cost=new_cost` - 重复2,3直至没有顶点可以访问. --- ```C# var frontier = new PriorityQueue(); frontier.put(start); path = new Array(); //每个顶点路径消耗 cost_so_far = new Array(); path[start] = 0; cost_so_far[start] = 0 while(frontier.length>0){ current = frontier.get(); if (current == goal) { break } //查找周围节点 for(next in graph.neighbors(current)) { var notInVisited = visited.indexOf(next)==-1; var new_cost = cost_so_far[current] + graph.cost(current, next); //没有访问过或者路径更近 if(notInVisited || new_cost < cost_so_far[next]) { cost_so_far[next] = new_cost; priority = new_cost; frontier.put(next, priority); path[next] = current; } } } ``` --- ####缺点 - 运行时间复杂度是:`T(n)=O(V^2)`,其中V为顶点个数。效率上并不高 - 目标查找不具有方向性 --- ###贪婪最佳优先搜索 - 我们采用每个顶点到目标顶点的距离进行排序 - 它的路径不是最优和最短的 - 跟bfs一样,遇到障碍物直接不能绕过去 - 启发式搜索 --- ```C# frontier = new PriorityQueue(); frontier.put(start, 0) came_from = new Array(); came_from[start] = 0; while(frontier.length>0){ current = frontier.get(); if (current == goal) { break; } for(next in graph.neighbors(current)) { var notInVisited = visited.indexOf(next)==-1; //没有访问过 if(notInVisited ) { //离目标的距离 ,距离越近优先级越高 priority = heuristic(goal, next); frontier.put(next, priority); came_from[next] = current; } } } //估值函数 function heuristic(a, b){ //离目标的距离 return abs(a.x - b.x) + abs(a.y - b.y) } ``` ####缺点 --- - 路径不是最短路径,只能是较优 - 在启发式搜索中,估价函数是十分重要的,采用了不同的估价可以有不同的效果 --- ###A*算法 - A*算法的优先队列排序方式基于F值 - F=cost(`顶点到起始顶点的距离`)+heuristic(`顶点到目标顶点的距离`) --- ```C# var frontier = new PriorityQueue(); frontier.put(start); path = new Array(); cost_so_far = new Array(); path[start] = 0; cost_so_far[start] = 0 while(frontier.length>0){ current = frontier.get(); if (current == goal) { break; } for(next in graph.neighbors(current)) { var notInVisited = visited.indexOf(next)==-1; var new_cost = cost_so_far[current] + graph.cost(current, next); //没有访问过而且路径更近 if(notInVisited || new_cost < cost_so_far[next]) { cost_so_far[next] = new_cost //队列优先级= new_cost(顶点到起始顶点的距离 )+heuristic(顶点到目标顶点的距离 ) priority = new_cost + heuristic(goal, next) frontier.put(next, priority) path[next] = current } } } function heuristic(a, b){ //离目标的距离 return abs(a.x - b.x) + abs(a.y - b.y) } ``` - 那么当F值相同时,如何更智能的选择格子呢?我们可以优先选择H值更小的那个格子。因为H值越小,代表它越接近目标,在当前格子到目标之间没有障碍物的情况下,这一定是最优的选择 --- ###B*算法 - 一种比A*算法更高效的算法,适用于游戏中怪物的自动寻路 --- ####流程 --- - 径直方向没有障碍物,径直向 E 走去 - 碰到障碍物,以障碍物格子为界,沿着障碍物边缘分别行走形成分支以搜索 - 走到终点,输出答案 --- - 它基本就是沿着墙走的,可以算是沿着障碍物,而且据传言,蟑螂进入一个锐角区域后便无法后退,很有可能就要和这个世界说再见了  - 前方没路,回头的路又被标记为了“走过”,根据寻路最优原理,是不能再走了的 - 因为在“锐角”中朝一个方向走的时候,前面三个方向都被挡住了 --- ###JPS --- - 对A寻路算法的一个改进,即在扩展搜索节点时,提出了更优化的策略 - A在扩展节点时会把节点所有邻居都考虑进去,这样openlist中点的数量会很多,搜索效率较慢 - 通过寻找跳点的方式,排除了大量不感兴趣的点,减少了openlist中搜索的点的数量,速度大大提高 --- ####强迫邻居(被迫邻居)定义 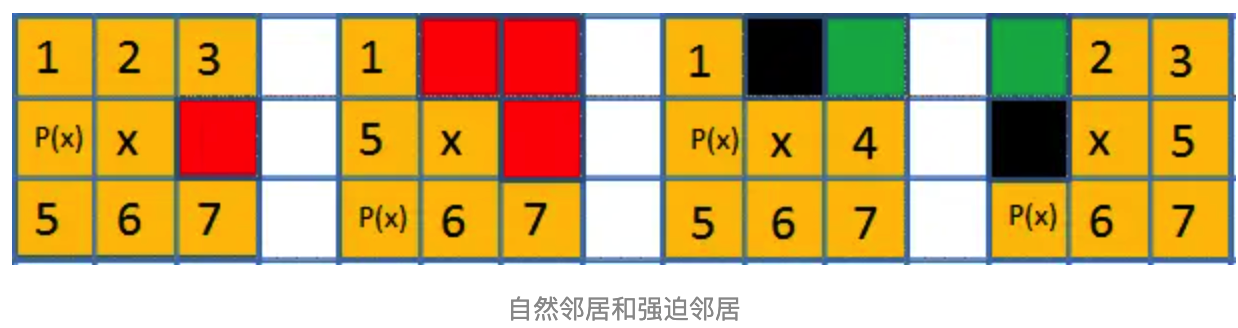 - 上图中`红色块`为节点x,基于前节点为P(x)的情况下的`自然邻居节点` - `被迫邻居`则是图中`绿色`的方块 - 首先被迫邻居的位置是基于P(x)、x、阻挡块的相对关系定的 --- ####跳点定义 --- - 节点y是起点或终点 - 节点y在当前搜索方向的前提下,有强迫邻居 - 当前搜索方向是斜向,且在y节点处,经过该斜向的水平分量或垂直分量方向移动可以找到跳点,那么当前节点y是跳点 ####搜索流程 --- - 若current方向是直线 - 如果current左后方不可走且左方可走,则沿current左前方和左方寻找跳点 - 如果current当前方向可走,则沿current方向寻找跳点 - 如果current右后方不可走且右方可走,则沿current右前方和右方寻找跳点 - 若current方向是斜线 - 如果当前方向的水平分量可走,则沿current方向的水平分量方向寻找跳点 - 如果当前方向可走,沿current方向寻找跳点 - 如果当前方向的垂直分量可走,则沿current方向的垂直分量方向寻找跳点 --- ###优化A*一般从以下四个方面着手 --- - openlist(开放集合) - 使用优先队列提升A*的速度 - 添加操作:O(logn) - 删除操作:O(logn) - 获取长度:O(1) - 判断是否存在:O(1) - 排序:O(logn) - 优化openlist改变A*的路径 - openlist的排序是稳定,第一次使用A*走出了路径1,那么下一次使用A*也会走出路径1 - getNeighbour优化 - 增加路径的随机性 - 为了消除获取邻居的优先次序,会在获取邻居的时候加上概率 - 寻找更优路径 - A*的眼界最多也就8个视野,如果你想让A*看的更远,可以在扩大A*眼界范围,也可以是周围两圈,三圈 - 眼界越大,就意味着A*要计算的节点也就越多,A*的速度一定会变慢,优点是可以让A*找到更优的路径 - JPS跳点搜索算法:通过减少邻居节点来提升速度,对邻居节点进行剪枝,删去不必要的邻居 - F=G+H+C启发式优化 - G:该点到起点的实际路径长度 - H:该点到终点估算的估计长度 - C:从当前节点走到该点的格外代价 - 减少拐点,如果A*拐弯,通过增大C的值来增大F的值,加C函数的时机也很重要,我一般把C函数加在G函数上,即在计算邻居节点的G函数时,就加上C函数。 ```C# /// <summary> /// 额外代价 /// </summary> /// <param name="current">当前节点</param> /// <param name="neighbor">邻居节点</param> /// <param name="goal">终点</param> /// <returns></returns> public double Cost(Node current,Node neighbor, Node goal) { Node parent = current.parent; // 起点 if (parent == null) return 0; // 走直线 if (neighbor.x == parent.x || neighbor.y == parent.y) return 0; // 拐向终点的点 if (neighbor.x == goal.x || neighbor.y == goal.y) return 1; // 普通拐点 return 2; } ``` - Map矩阵优化 - 分层优化提升速度--HPA - 对于地图比较大的场景,进行一次长距离的寻路不能直接就在整个地图上跑一次A*,因为单次路径搜索的开销可能非常大 - 把整个地图按区域来进行一次划分: - `local A*`,即在单个区域内部进行 A* 算法 - `tile A*`,即在区域间进行 A* 算法 - 如果路径搜索的源点和目标点都在同一个区域内部,那么 local A* 即可;而如果分别位于两个不同的区域,那么首先尝试找到两块区域的通路,然后每次得出这一次长路径需要经过的诸多区域 0614学习 0922学习