A-Star(A*)寻路算法原理与实现 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/385733813) 前言 -- 远古时期,自动寻路的功能就是我们国产 MMORPG 游戏的特色之一,并且被很多 “清高” 的玩家所诟病。如果做得不好,就可能出现下图这样的尴尬局面(站在玩家的角度这个寻路肯定是无法接受的。站在程序员的角度,能寻到就不错了,你行你上啊!):  实际上除了玩家自己控制的角色以外,很多 NPC 或者机器人(AI)同样需要自动寻路的功能来达到与玩家交互的功能。例如吃鸡游戏中,机器人在城镇中跑毒就需要自动寻路,不然可能就被墙卡死了。 那么我们要怎么来计算当前位置到目标位置的最短路径呢?如今已经有各种各样的寻路算法可以帮助到我们。对于一些**动态场景**,比如运行时会动态生成障碍物或者障碍物可以移动的场景可以使用 **D-Star**(D*)算法。对于**静态场景**,也就是场景固定的情况可以使用 **Dijkstra** 算法,**A-Star**(A*)算法。 对于上述这些算法如今都有一些比较完善的插件,我们只需要左点右点就可以实现寻路的功能,此外 Unity 也提供了 [NavMeshComponents](https://github.com/Unity-Technologies/NavMeshComponents) 用于寻路。本篇主要就是简单的介绍下 A * 算法的概念以及代码逻辑,只有了解了最基础的寻路算法,才能更好的理解更牛逼的寻路算法嘛,例如 [Jump Point Search](https://zhuanlan.zhihu.com/p/290924212)。 Demo 工程如下: [luckyWjr/Demo](https://github.com/luckyWjr/Demo/tree/master/Assets/A-Star) 效果图如下,绿色代表玩家位置,红色代表终点,黄色路径即使找到的最短路径。 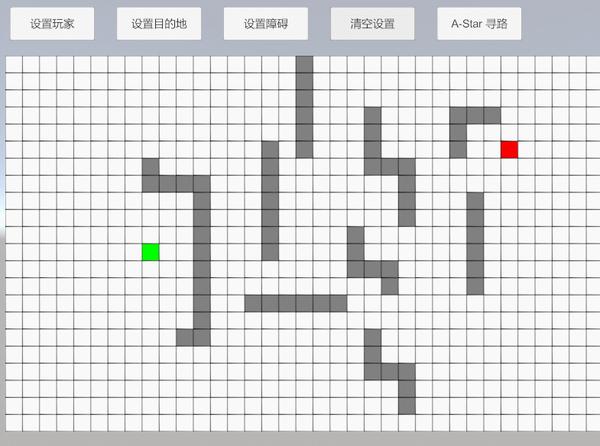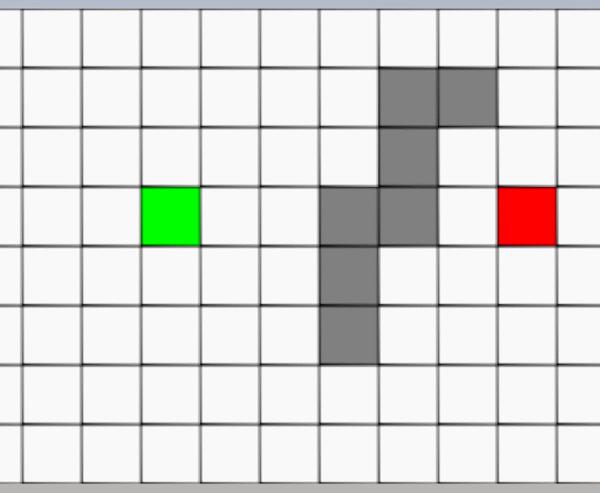 在 Demo 中 Panel 下挂了 UIMapController 组件,可以设置格子大小,估价函数类型,是否显示格子内的信息(参考上上图)以及是否逐步操作。 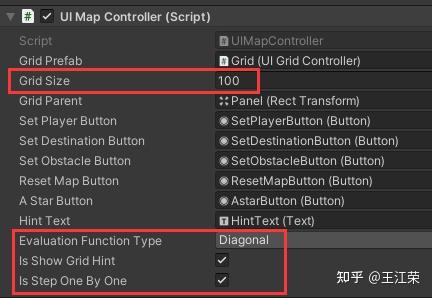 A * 寻路算法 -------- ### 基于格子(Grid) A * 算法是一种基于格子(Grid)的寻路算法,也就是说会把我们的地图看作是由 w*h 个格子组成的,因此寻得的路径也就是由一连串相邻的格子所组成的路径。 为了方便展示和理解,就用 UGUI 绘制了一个网格用于模拟地图,如下:  灰色格子代表障碍物,我们要找到从绿点到红点的最短路径。 注:非基于格子的寻路可以使用**基于采样**(Sampling Based)的算法,例如 **RRT-Connect**。 ### 启发式(heuristic) 我们知道一个格子可以往八个方向移动,如下图:  那么往哪个格子走可以让我们更接近目标呢?例如如果我们的绿点一直往左走,岂不是南辕北辙了。 如果我们能在每次移动前做一个评估,是不是会减少误入歧途的次数呢?例如原本我们红绿两点的直线距离为 5 个格子(不考虑障碍物),若向左走后距离变为 6,而向右走后变为 4,那么理论上我们应该向右走才能更快到达红点。 通过评估来找到合适路径的算法我们称之为启发式算法,即**优先搜索最有可能产生最佳路径的格子**。A * 正是这样的算法,因此可以避免掉很多歪路(不必要的计算),提高效率。 ### 估价函数 前面我们说了要对每个可能到达的格子进行估价,来判断应该先往哪个格子走,因此我们需要一个估价函数来计算。 对于任意一个格子 n,其估价函数如下: > f(n) = g(n) + h(n) **其中 g(n) 指的是从起始格子到格子 n 的实际代价,而 h(n) 指的是从格子 n 到终点格子的估计代价。** 举个例子,我们来看看下面三个格子 f(n) 的值:  * 格子 1:绿点到 1 要行动移动一格,因此 g(1)=1,格子 1 到红点的直线距离为 6 个格子,因此 h(1)=6,所以 f(1)=1+6=7 。 * 格子 2:绿点到 2 要行动移动一格,因此 g(2)=1,格子 2 到红点的直线距离为 4 个格子,因此 h(2)=4,所以 f(2)=1+4=5 。 * 格子 3:绿点到 3 要对角移动,因此 g(1)=  ,格子 1 到红点的直线距离为  (直角三角形斜边),因此 h(3)=  ,所以 f(3)=  =5.54 。 可以看出,f(n) 的值基本代表着从起点格子到格子 n 再到终点这一段路径的长度。由于 f(2) < f(3) < f(1),因此我们优先应该考虑去往格子 2 的情况。 在上面,我们 h(n) 指的是格子与格子间的直线距离,也就是**欧几里得距离**,然而它有两个**弊端**: * 计算过程中伴随着平方与开根号运算,并且需要使用浮点数,性能差。 * 实际过程中格子 3 并不能直接平滑的移动到红色格子,而需要水平 + 对角移动结合。即若没有障碍物,实际的 h(3) =  +3,而不是  。也就是说用欧几里得距离时, **h(n) 的值永远小于或等于格子 n 到终点的最短实际距离。** 因此针对上述这些问题,我们 h(n) 用的更多的是曼哈顿距离或者是对角线 + 直线的距离。 欧几里得距离示意图:  ### 曼哈顿距离 曼哈顿距离简单来说就是**只准水平或垂直移动**的最短距离,示意图如下: 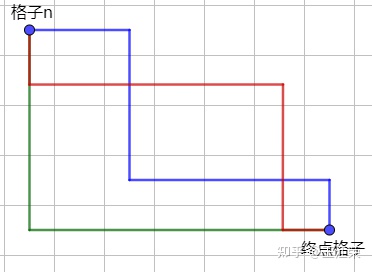 图中从格子 n 到终点有三条不同的路径,但是它们的总长度确是相同的,这个长度也就是我们的曼哈顿距离,也就是两个格子水平方向的差值与竖直方向的差值和。 这样相比欧几里得距离,只需要计算加减法,并且连浮点数都不需要。但是由于我们的格子可以对角线移动,因此不考虑障碍物的话,或者障碍物在两个格子形成的包围盒内,**曼哈顿距离肯定大于或等于格子 n 到终点的最短实际距离。** ### 对角线 + 直线距离 既然我们可以对角线移动,那么我们就可以根据水平方向的差值与竖直方向的差值中较小的那个值,计算出对角线,然后再平移。示意图如下: 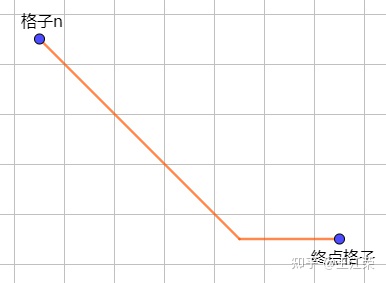 这样不考虑障碍物的情况下,肯定**等于格子 n 到终点的最短实际距离。** 但是由于计算对角线同样需要开根号以及浮点数。为了加快计算,我们可以**假设两个格子间的距离为 10,然后直接认为对角线距离为 14(不是根号 20 了)**,这样就可以避免浮点数和根号运算了。 ### h(n) 的影响 直接来看一个例子,如下图: 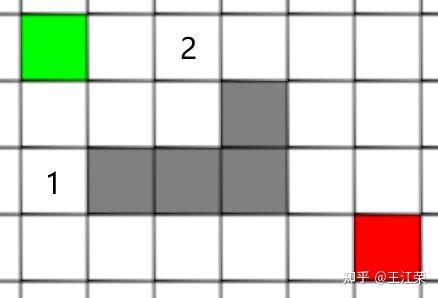 图中 g(1)=g(2)=20,若 h(n) 使用曼哈顿距离,则 h(1)=h(2)=60,即 f(1)=f(2),导致我们无法判断出走 1 和走 2 哪个更好。但是若使用对角线距离,则 h(1)=60,h(2)=42,f(1)>f(2),因此我们下一步要走 2。 实际上走 2 才是最短的路径,但是由于有障碍物,格子 2 到红格子的实际距离为 10+14+14+10=48(右 -> 右下 -> 右下 -> 下),可以发现这种情况下:曼哈顿距离 > 实际距离 > 对角线距离。 再来看一个例子: 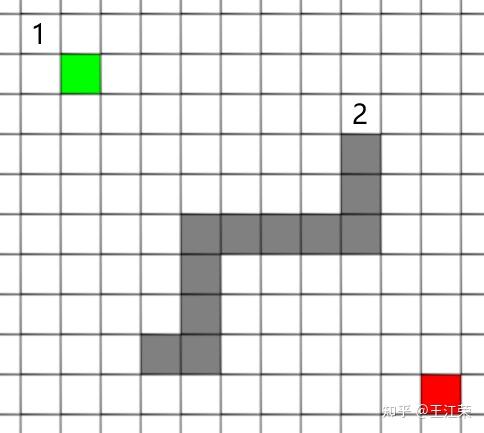 若使用曼哈顿距离,f(1)=g(1)+h(1)=14+190=204,f(2)=g(2)+h(2)=74+90=184,就是说我宁可考虑格子 2 也不会去考虑格子 1。 但是使用对角线距离,f(1)=g(1)+h(1)=14+136=150,f(2)=g(2)+h(2)=74+78=152,那就变得格子 1 要优先考虑。 两种 h(n) 得到的路径如下: 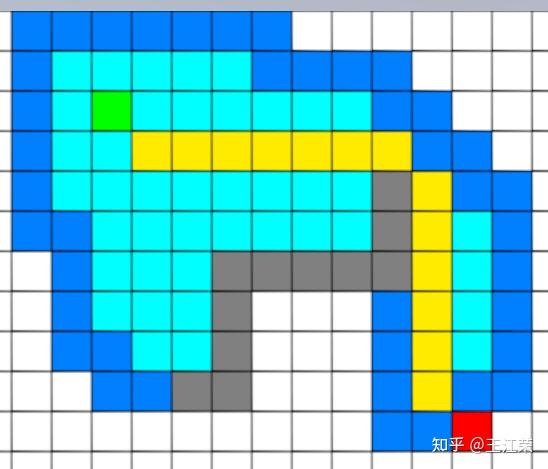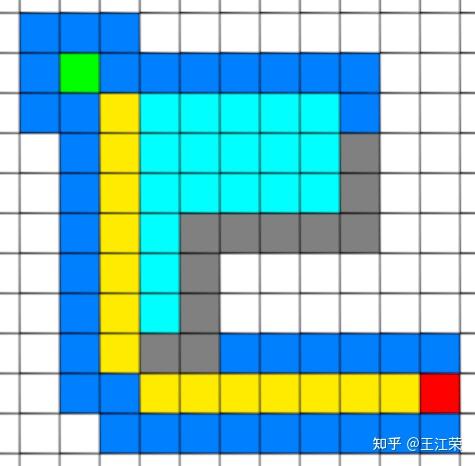 可以发现,对角线距离的结果才是最短的路径,但是它会计算更多的格子(图中两种蓝色的格子就是要计算的格子)。 总结来说: * 如果 h(n) <= n 到终点的实际距离,A * 算法可以找到最短路径,但是搜索的点数多,搜索范围大,效率低。 * 如果 h(n) > n 到终点的实际距离,搜索的点数少,搜索范围小,效率高,但是得到的路径并不一定是最短的。 * h(n) 越接近 n 到终点的实际距离,那么 A * 算法越完美。(个人理解是如果用曼哈顿距离,那么只需要找到一条长度小于等于该距离的路径就算完成任务了。而使用对角线距离就要找到一条长度大于等于对角线距离且最短的路径才行。) * 若 h(n)=0,即 f(n)=g(n),A * 算法就变为了 Dijkstra 算法(Dijstra 算法会毫无方向的向四周搜索)。 * 若 h(n) 远远大于 g(n) ,那么 f(n) 的值就主要取决于 h(n),A * 算法就演变成了 BFS 算法。 **因此在启发式搜索中,估价函数是十分重要的,采用了不同的估价可以有不同的效果。** ### 具体寻路过程 一些基本的概念介绍完后,我们来看看怎么 A * 算法的具体寻路是怎么样的,基本上就是说,哪些格子我们要去估价,然后这些格子按什么顺序去估价。 我们从最简单的场景入手来理解,如下图: 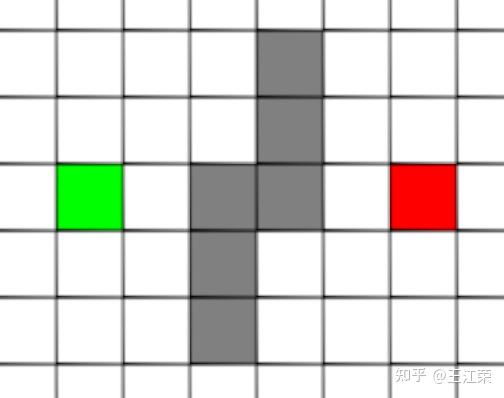 **第一步:**因为我们的绿点可以往周边 8 个格子移动,那么我们就要用估价函数计算它周边格子的值,来看看往哪走比较好,得到结果如下(使用对角线距离估价): 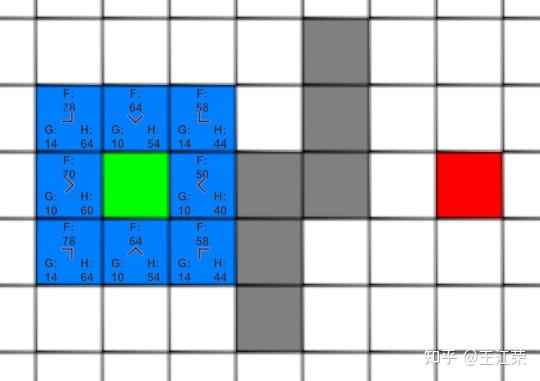 因为我们是通过绿色格子计算得到这 8 个格子的,因此它们都指向绿色格子(格子中的箭头),或者称绿色格子是它们的 parent。 **第二步:**我们找到第一步 8 个格子中 f(n) 值最小的格子(格子 0),然后再计算它周边格子的 f(n),如下图: 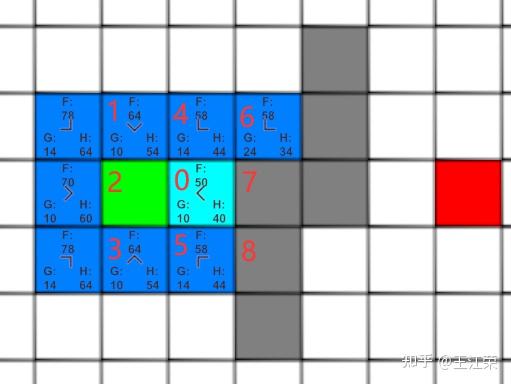 此时格子 0 周边格子的 g(n) 应该是 g(0) 的值加上自己到格子 0 的距离。例如格子 1 此时的 g(1) 应该为 g(0)+14=24,即 2-0-1 的顺序。但是由于格子 1 在第一步已经算过了,当时 g(1)=10,2-1 的顺序。这里我们**要用较小的那个值,因为 g 值小,说明路径短**。格子 3,4,5 同理。而格子 6 之前没有计算过,因此 f(6)=g(6)+h(6)=(g(0)+14)+h(h),顺序 2-0-6。 格子 7,8 由于是障碍物,直接不管就行。格子 2 由于之前已经计算过它周边了,没有再计算它的意义了,也不用管。 **第三步:**我们从剩下的 8 个深蓝色的格子中再找出 f(n) 最小的格子,由于有 3 个等于 58 的格子,我们随便取一个计算它周边的格子,如下图: 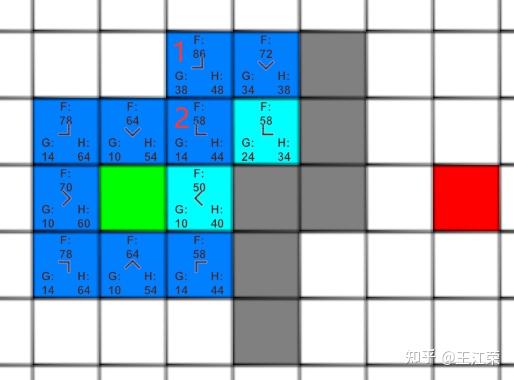 这里可以发现,格子 1 的 g 值并不是最小的,但是不要紧,当我们后面计算到格子 2 时,会更新格子 1 的 g 值(前面说了会用较小的 g 值),并且箭头指向格子 2。 **第四步... 第 n 步**:一直找出深蓝色格子中的 f(n) 最小的格子,然后计算周边格子的估价值。 **最后一步:**当我们发现某个格子(格子 1)周边有个格子是终点格子时,就说明我们找到了到终点的最短路径。 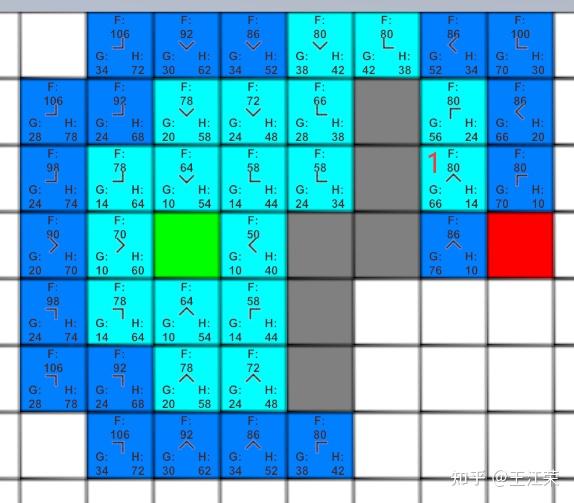 我们只需要根据格子 1 的箭头指向一直往前就可以得到完整的路径: 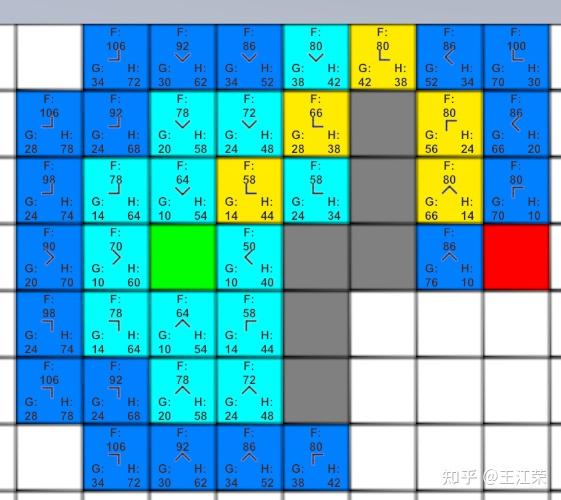 A * 代码 ------ 逻辑理清楚,代码写起来就非常的简单了,这里就简单贴一下比较关键的代码。更完整的代码可以看开头的 github 链接。 首先由于我们要记录格子的估价值,以及它的 parent,因此需要一个类来存储这些值: ``` public class Node { Int2 m_position;//下标 public Int2 position => m_position; public Node parent;//上一个node //角色到该节点的实际距离 int m_g; public int g { get => m_g; set { m_g = value; m_f = m_g + m_h; } } //该节点到目的地的估价距离 int m_h; public int h { get => m_h; set { m_h = value; m_f = m_g + m_h; } } int m_f; public int f => m_f; public Node(Int2 pos, Node parent, int g, int h) { m_position = pos; this.parent = parent; m_g = g; m_h = h; m_f = m_g + m_h; } } ``` 然后我们需要两个数据结构 **open** 和 **close** 来存储格子,在之前的过程中,将要被计算周边格子的格子都存储在 open 当中,当周边格子计算完后,就可以把这个格子存储到 close 中,然后把它周边的格子再放入到 open 中。 例如一开始我们把起始格子放入 open 中,然后从 open 中取出 f(n) 值最小的一个格子(这里使用 C# 的 Linq 排序)去计算它周边的格子。因为此时 open 中只有一个元素,因此就是计算起始格子周边的格子。接着把起始格子周边 8 个格子加入到 open 中,把起始格子从 open 中删除加入到 close 中。 然后再从 open 中找出 f(n) 最小的格子,将它周边的格子加入到 open 中,并将自己从 open 中删除加入到 close 中,如此循环。 再每次计算周边格子的时候,需要判断这些格子是否超出边界,是否是障碍物,是否在 close 中,这三种情况不需要再处理该格子了。如果格子已经在 open 中,就要像之前所说的,若新的 g 值小于老的 g 值,就要更新 g、f 以及 parent 的值。 最后如果周边某个格子是终点(代表寻路完成)或者 open 列表为空(代表可用格子全部计算完,但却没找到终点,死路一条!),则结束寻路过程。 可以发现整个过程都要频繁的用到了增删以及查询,因此 open 和 close 使用了 Dictionary。 代码如下: ``` public class AStar { static int FACTOR = 10;//水平竖直相邻格子的距离 static int FACTOR_DIAGONAL = 14;//对角线相邻格子的距离 bool m_isInit = false; public bool isInit => m_isInit; UIGridController[,] m_map;//地图数据 Int2 m_mapSize; Int2 m_player, m_destination;//起始点和结束点坐标 EvaluationFunctionType m_evaluationFunctionType;//估价方式 Dictionary<Int2, Node> m_openDic = new Dictionary<Int2, Node>();//准备处理的网格 Dictionary<Int2, Node> m_closeDic = new Dictionary<Int2, Node>();//完成处理的网格 Node m_destinationNode; public void Init(UIGridController[,] map, Int2 mapSize, Int2 player, Int2 destination, EvaluationFunctionType type = EvaluationFunctionType.Diagonal) { m_map = map; m_mapSize = mapSize; m_player = player; m_destination = destination; m_evaluationFunctionType = type; m_openDic.Clear(); m_closeDic.Clear(); m_destinationNode = null; //将起始点加入open中 AddNodeInOpenQueue(new Node(m_player, null, 0, 0)); m_isInit = true; } //计算寻路 public IEnumerator Start() { while(m_openDic.Count > 0 && m_destinationNode == null) { //按照f的值升序排列 m_openDic = m_openDic.OrderBy(kv => kv.Value.f).ToDictionary(p => p.Key, o => o.Value); //提取排序后的第一个节点 Node node = m_openDic.First().Value; //因为使用的不是Queue,因此要从open中手动删除该节点 m_openDic.Remove(node.position); //处理该节点相邻的节点 OperateNeighborNode(node); //处理完后将该节点加入close中 AddNodeInCloseDic(node); yield return null; } if(m_destinationNode == null) Debug.LogError("找不到可用路径"); else ShowPath(m_destinationNode); } //处理相邻的节点 void OperateNeighborNode(Node node) { for(int i = -1; i < 2; i++) { for(int j = -1; j < 2; j++) { if(i == 0 && j == 0) continue; Int2 pos = new Int2(node.position.x + i, node.position.y + j); //超出地图范围 if(pos.x < 0 || pos.x >= m_mapSize.x || pos.y < 0 || pos.y >= m_mapSize.y) continue; //已经处理过的节点 if(m_closeDic.ContainsKey(pos)) continue; //障碍物节点 if(m_map[pos.x, pos.y].state == GridState.Obstacle) continue; //将相邻节点加入open中 if(i == 0 || j == 0) AddNeighborNodeInQueue(node, pos, FACTOR); else AddNeighborNodeInQueue(node, pos, FACTOR_DIAGONAL); } } } //将节点加入到open中 void AddNeighborNodeInQueue(Node parentNode, Int2 position, int g) { //当前节点的实际距离g等于上个节点的实际距离加上自己到上个节点的实际距离 int nodeG = parentNode.g + g; //如果该位置的节点已经在open中 if(m_openDic.ContainsKey(position)) { //比较实际距离g的值,用更小的值替换 if(nodeG < m_openDic[position].g) { m_openDic[position].g = nodeG; m_openDic[position].parent = parentNode; ShowOrUpdateAStarHint(m_openDic[position]); } } else { //生成新的节点并加入到open中 Node node = new Node(position, parentNode, nodeG, GetH(position)); //如果周边有一个是终点,那么说明已经找到了。 if(position == m_destination) m_destinationNode = node; else AddNodeInOpenQueue(node); } } //加入open中,并更新网格状态 void AddNodeInOpenQueue(Node node) { m_openDic[node.position] = node; ShowOrUpdateAStarHint(node); } void ShowOrUpdateAStarHint(Node node) { m_map[node.position.x, node.position.y].ShowOrUpdateAStarHint(node.g, node.h, node.f, node.parent == null ? Vector2.zero : new Vector2(node.parent.position.x - node.position.x, node.parent.position.y - node.position.y)); } //加入close中,并更新网格状态 void AddNodeInCloseDic(Node node) { m_closeDic.Add(node.position, node); m_map[node.position.x, node.position.y].ChangeInOpenStateToInClose(); } //寻路完成,显示路径 void ShowPath(Node node) { while(node != null) { m_map[node.position.x, node.position.y].ChangeToPathState(); node = node.parent; } } //获取估价距离 int GetH(Int2 position) { if(m_evaluationFunctionType == EvaluationFunctionType.Manhattan) return GetManhattanDistance(position); else if(m_evaluationFunctionType == EvaluationFunctionType.Diagonal) return GetDiagonalDistance(position); else return Mathf.CeilToInt(GetEuclideanDistance(position)); } //获取曼哈顿距离 int GetDiagonalDistance(Int2 position) { int x = Mathf.Abs(m_destination.x - position.x); int y = Mathf.Abs(m_destination.y - position.y); int min = Mathf.Min(x, y); return min * FACTOR_DIAGONAL + Mathf.Abs(x - y) * FACTOR; } //获取对角线距离 int GetManhattanDistance(Int2 position) { return Mathf.Abs(m_destination.x - position.x) * FACTOR + Mathf.Abs(m_destination.y - position.y) * FACTOR; } //获取欧几里得距离,测试下来并不合适 float GetEuclideanDistance(Int2 position) { return Mathf.Sqrt(Mathf.Pow((m_destination.x - position.x) * FACTOR, 2) + Mathf.Pow((m_destination.y - position.y) * FACTOR, 2)); } public void Clear() { foreach(var pos in m_openDic.Keys) { m_map[pos.x, pos.y].ClearAStarHint(); } m_openDic.Clear(); foreach(var pos in m_closeDic.Keys) { m_map[pos.x, pos.y].ClearAStarHint(); } m_closeDic.Clear(); m_destinationNode = null; m_isInit = false; } } ``` 一些参考: [Amit’s A* Pages](http://theory.stanford.edu/~amitp/GameProgramming/) Asset简介 Unity里的Procedural Animation