AVL树 agile Posted on Jul 14 2023 数据结构与算法 yukiyama --- title: AVL树 tags: - AVL树 - 平衡二叉树 - 旋转操作 categories: 算法与数据结构 description: 本文介绍一种最早提出的自平衡二叉查找树 –– AVL树。重点展现如何设计一个AVL树类,分析主要方法的代码实现,并给出该类的完整实现代码。 cover: >- https://raw.githubusercontent.com/iyukiyama/pics/master/hexo-iyukiyama/site_img/posts/algorithms/avl-tree-bg.png katex: true abbrlink: avl-tree keywords: top_img: comments: --- # AVL树 (树ADT连载 4/13) > - 可在作者的 [github仓库](https://github.com/iyukiyama/leetcode-posts) 中获取本文和其他文章的 markdown 源文件及相关代码。 > > - 欢迎评论或仓库 PR 指出文章错漏或与我讨论相关问题,我将长期维护所有文章。 > - 所有文章均用 Typora 完成写作,可使用 Typora 打开文章 md 文件,以获得最佳阅读体验。 🌲🌲🌲 **一起手写一棵完整的 AVL 树。** ❗️ **【NEW】** ❗️ - 9-15: [红黑树从入门到看开](https://leetcode.cn/circle/discuss/SwgIJV/) 这是小白 yuki 推出的「树ADT」系列文章的第 4 篇 (4/13) 。 *** > $keywords$ : > > AVL树 / 单旋转与双旋转 / 绝对平衡 本文介绍一种最早提出的自平衡二叉查找树 –– AVL树。本文重点在于展现如何设计一个AVL树类,分析主要方法的代码实现,并给出该类的完整实现代码。期待读者学习之后 **能够自己写出一个方法较为完备的AVL树类** 。 *** yuki的其他文章如下,欢迎阅读指正! > 如下所有文章同时也在我的 github [仓库](https://github.com/iyukiyama/leetcode-posts) 中维护。 | 文章 | [发布时间] 字数/览/藏/赞 (~2022-10-20) | | ------------------------------------------------------------ | ---------------------------------------- | | [十大排序从入门到入赘](https://leetcode.cn/circle/discuss/eBo9UB/) 🔥🔥🔥 | [20220516] 2.5万字/64.8k览/3.7k藏/937赞 | | [二分查找从入门到入睡](https://leetcode.cn/circle/discuss/ooxfo8/) 🔥🔥🔥 | [20220509] 2.3万字/38.4k览/2.1k藏/503赞 | | [并查集从入门到出门](https://leetcode.cn/circle/discuss/qmjuMW/) 🔥🔥 | [20220514] 1.2万字/17.9k览/1.0k藏/321赞 | | [图论算法从入门到放下](https://leetcode.cn/circle/discuss/FyPTTM/) 🔥🔥 | [20220617] 5.6万字/19.9k览/1.3k藏/365赞 | | 树ADT系列 (预计13篇) | 系列文章,连载中 | | 3. [二叉查找树](https://leetcode.cn/circle/discuss/wPzlSb/) | [20220801] 5千字 | | 4. [AVL树](https://leetcode.cn/circle/discuss/zbwD3p/) | [20220817] 5千字 | | 5. [splay树](https://leetcode.cn/circle/discuss/BCK17f/) | [20220817] 5千字 | | 6. [红黑树从入门到看开](https://leetcode.cn/circle/discuss/SwgIJV/) 🔥🤯🤯🤯 | [20220915] 3万字/5.3k览/269藏/72赞 | | 10. [树状数组从入门到下车](https://leetcode.cn/circle/discuss/qGREiN/) 🔥🤯 | [20220722] 1.4万字/5.8k览/196藏/72赞 | | 11. [线段树从入门到急停](https://leetcode.cn/circle/discuss/H4aMOn/) 🔥🤯 | [20220726] 2.5万字/8.7k览/481藏/138赞 | | [图论相关证明系列](https://leetcode.cn/circle/discuss/GV0JrV/) | 系列文章 | | 1. [Dijkstra正确性证明](https://leetcode.cn/circle/discuss/jJQn7V/) 🤯 | [20220531] | | 2. [Prim正确性证明](https://leetcode.cn/circle/discuss/VVEc8f/) 🤯 | [20220919] | | 3. [Bellman-Ford及SPFA正确性证明](https://leetcode.cn/circle/discuss/xeEwYl/) | [20220602] | | 4. [Floyd正确性证明](https://leetcode.cn/circle/discuss/Nbzix4/) | [20220602] | | 5. [最大流最小割定理证明](https://leetcode.cn/circle/discuss/tMIy36/) 🤯🤯 | [20220719] | | 6. [Edmonds-Karp复杂度证明](https://leetcode.cn/circle/discuss/tN3sZc/) 🤯🤯 | [20220515] | | 7. [Dinic复杂度证明](https://leetcode.cn/circle/discuss/T9Xa1R/) 🤯🤯 | [20220531] | *** [2022-10-17] - 旋转后结点高度更新代码有误,`Math.max()` 取得左右子树中较高者的高度后还要加 1。感谢匿名用户提醒!🙏 *** [TOC] *** ### AVL树 对于二叉查找树的插入、删除、查找等操作,时间复杂度为 $O(logn)$ 的前提是 **保持树的平衡** ,即保持树的高度为 $logn$ 。在 [二叉查找树](https://leetcode.cn/circle/discuss/wPzlSb/) 一文的删除结点的操作中,我们总是 **删除目标结点右子树中的最小结点** ,可以预见多次删除操作后将使树呈现 **左高右低的倾向** 。而一旦树不平衡,插入、删除、查找等操作将无法达到 $O(logn)$ 的复杂度,于是我们自然会想如何在多次删除操作后,树总能够保持平衡。若一棵 BST 在操作后总能保持平衡,我们称其为 **平衡 BST** 。 **AVL 树是最早提出的自平衡二叉查找树** 。 AVL 树以 **「旋转 (rotation)」** 操作保证 **任意结点的左右子树高度差不超过 1**,使得树的深度总保持为 $O(logn)$ 。下图左侧的树是 AVL 树,右侧的树则不是 AVL 树,在结点 7 处失衡。  > AVL (Adelson-Velsky and Landis Tree) 树由 G.M. Adelson-Velsky 和E.M. Landis于1962年的 [论文](https://zhjwpku.com/assets/pdf/AED2-10-avl-paper.pdf) 中首次介绍。 > > 文本内容为 Mark Allen Weiss 所著 [数据结构与算法分析:Java语言描述](https://awesome-programming-books.github.io/algorithms/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E5%88%86%E6%9E%90%EF%BC%9AJava%E8%AF%AD%E8%A8%80%E6%8F%8F%E8%BF%B0.pdf) 相关章节的整理和总结。代码亦来自该书,略作改动。 <br /> #### 旋转 在上图 AVL 树中插入 6 时, 6 将作为 7 的左子结点被插入,这将破坏结点 8 的平衡 (8的左子树与其右子树高差为 2)。AVL 树通过旋转操作能够恢复失衡结点的平衡,本节详细讲解此操作的细节。 考虑插入一个结点 $x$ 后,平衡被破坏的结点 $y1, y2,…$ ,这些结点只可能在 $x$ 到根结点路径上,因此 **只需沿着此路径恢复平衡即可** 。更进一步地,不难证明,只需在第一个平衡被破坏的结点 $y$ ( $x$ 到根结点方向)上重新平衡这棵树,即能保证整棵树恢复为 AVL 树。 插入情况必为如下四情形种之一: ``` 情形1(左-左): 插入点在 y 的左儿子的左子树 情形2(左-右): 插入点在 y 的左儿子的右子树 情形3(右-左): 插入点在 y 的右儿子的左子树 情形4(右-右): 插入点在 y 的右儿子的右子树 ``` 其中 1 和 4,2 和 3 关于 $y$ 镜像对称,所以实际只有两种情况,但从编程角度来看需要分别处理这四种情形。对于发生在外侧的情况 (左-左,右-右) ,需要通过 **单旋转** 恢复平衡,对于发生在内侧的情况 (左-右,右-左) ,需要通过 **双旋转** 恢复平衡。 > 许多资料将本节介绍的左单旋、右单旋、左右双旋、右左双旋分别称作 zag, zig, zag-zig, zig-zag 操作。zig 和 zag 原意并无左右之分,为了避免歧义,本文不采用这种称呼,读者只需了解即可。在「伸展树」一节中还会有「一字型」的左左双旋和右右双旋,分别被称为 zag-zag 和 zig-zig ,也仅需了解即可。 <br /> ##### **单旋转** **右单旋转 (情形1):** 如下,左侧的树是在 $k2$ 的左儿子 $k_1$ 的左子树中插入结点后导致 $k2$ 失去平衡 ( $k2$ 左子树比右子树深 2 层)。  上左图中 $X$ , $Y$ , $Z$ 的高度如此表现的依据: $Y$ 不可能与当前的 $X$ 在同一水平上,否则在插入前即失衡。$Y$ 也不可能与 $Z$ 在同一水平上,否则插入后先失衡的是 $k1$(在插入结点通往根路上第一个失衡)。 单旋转操作方法: 在失衡结点 $k2$ 和其左子结点 $k1$ 之间旋转。如图,核心操作为 `k2.left = k1.right`,`k1.right = k2` ,可以形象地描述为将 $k1$ 提起,$k_2$ 下沉的同时 $Y$ 被抖落到 $k2$ 的左侧。旋转方向为右侧,即顺时针方向,且只有一次旋转操作,因此称为 **右单旋转** 。旋转后以 $k2$ 和 $k1$ 为根结点的树的高度也需要实时调整( $height$ 是 $AvlNode$ 类的属性)。如下是该左-左单旋转的代码实现。 ```java private AvlNode<E> rotateRight(AvlNode<E> k2){ // 传入失衡结点 AvlNode<E> k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = Math.max(height(k2.left), height(k2.right)) + 1; // 调整k2高度 k1.height = Math.max(height(k1.left), height(k1.right)) + 1; // 调整k1高度 return k1; // 返回调整后原失衡处结点 (已变为 k1) } ``` 如图调整,将 $k1$ 作为调整后树的根结点,$X$ 上移 1 层,$Y$ 深度不变,$Z$ 下移 1 层,调整后 $XYZ$ 深度相同,树高度恢复为插入前的高度。 <br /> **左单旋转(情形4):** 如下,左侧的树在 $k1$ 的右儿子 $k_2$ 的右子树中插入结点后导致 $k1$ 失去平衡 ( $k1$ 右子树比左子树深 2 层)。  恢复平衡的旋转操作与左-左单旋转类似,核心操作为 `k1.right = k2.left`,`k2.left = k1` 。旋转方向为左侧,即逆时针方向,且只有一次旋转操作,因此称为 **左单旋转** 。以下给出右-右单旋转的代码实现。 ```java private AvlNode<E> rotateLeft(AvlNode<E> k1){ // 传入失衡结点 AvlNode<E> k2 = k1.right; k1.right = k2.left; k2.left = k1; // 调整平衡后更新k1,k2的高度 k1.height = Math.max(height(k1.left), height(k1.right)) + 1; k2.height = Math.max(height(k2.left), height(k2.right)) + 1; return k2; // 返回调整后原失衡处结点 (已变为 k2) } ``` <br /> ##### **双旋转** **左右双旋转(情形2):** 如下图左侧的树,在 $k2$ 的左儿子 $k1$ 的右子树中插入结点后导致 $k2$ 失衡 ( $k2$ 的左子树比右子树高 2)。 对于情形2和情形3,单旋转无法恢复平衡。如下图,执行一次单旋转后 $k1$ 的右子树比左子树高 2,平衡未恢复。恢复此情形的平衡需采用 **「双旋转」** 操作。  双旋转操作方法: 将上述左-右失衡情形 (情形2) 表示为下图。导致失衡的结点插入位置为 $k1$ 的右子树,因此可以表示为 $k2$ 及其左右子树的结构。 如前述,单旋转将 $k1$ 作为根无效,因此考虑将 $k2$ 作为根,将 $k2$ 的左子树 $B$ 作为 $k1$ 的右子树,$k2$ 的右子树 $C$ 作 为$k3$ 的左子树。然后 $k2$ 的左右儿子分别更新为 $k1$ , $k3$ 。如下图,平衡恢复。该双旋转实际上可以通过对 $k1$ 执行一次左单旋转,再对 $k3$ 执行一次右单旋转实现。可以看到代码实现十分简洁。 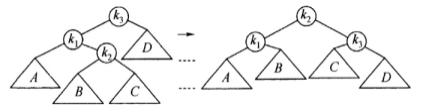 ```java /** * 左右双旋 * 因k2的左子结点的内侧子树,即k2的左子结点的右子树导致k2失衡。 * 对k2执行一次右单旋转后仍然在k1处(新根)失衡,因此考虑展开一开始导致失衡的k1右子树, * 做如下转换(总是以中序遍历的顺序标注结点,注意k1,k2,k3位置变化)。 * 因为不知道是B或C中的哪一棵导致失衡(比D深2层),所以将B,C画成比D深1.5。 * 依次执行如下两次单旋转后可恢复原失衡处的平衡。 * 1. 对k1(k3.left)执行左单旋转。 * 2. 对k3执行右单旋转。 * * k2 k3 * / \ / \ * k1 /\ 转换为 k1 /\ * / \ /__\ ====> / \ /__\ * /\ /\ Z /\ k2 D * /__\ / \ /__\ / \ * X / \ A /\ /\ * /______\ / \ / \ * Y /____\/____\ * B C * k3 k2 * / \ / \ * 对k1执行 k2 /\ 对k3执行 K1 K3 * 一次左单旋转 / \ /__\ 一次右单旋转 / \ / \ * =====> k1 /\ D ====> /\ /\ /\ /\ * / \ / \ /__\ / \ / \ /__\ * /\ /\ /____\ A /____\ /____\ D * /__\ / \ C B C * A /____\ * B */ private AvlNode<E> rotateLeftRight(AvlNode<E> k3){ // 传入失衡结点 k3.left = rotateLeft(k3.left); return rotateRight(k3); } ``` <br /> **右-左双旋转(情形3):** 如下图左侧的树,在 $k_1$ 的右儿子 $k_3$ 的左子树中插入结点后导致 $k_1$ 失衡 ( $k_1$ 的右子树比左子树高 2)。 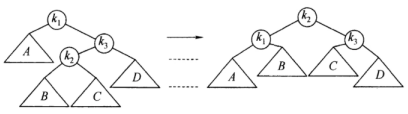 恢复平衡的旋转操作与左右双旋转类似,以下给出右左双旋转的代码实现。 ```java private AvlNode<E> rotateRightLeft(AvlNode<E> k1){ k1.right = rotateRight(k1.right); return rotateLeft(k1); } ``` <br /> #### AVL树类架构 以下是AVL查找树类 `AvlTree` 的架构。 | 类成员/方法 | 描述 | | --------------------------------------------------- | ------------------------------------------------------------ | | `private AvlNode<E> root` | 字段,AVL树的根结点 | | `private static final int ALLOWED_IMBALANCE = 1` | 常量字段,结点的失衡判定值,大于此值则失衡 | | `public AvlTree()` | 无参构造器,$root$ 初始化为 $null$ | | `public void makeEmpty()` | 树置空 | | `public boolean isEmpty()` | 判断树是否为空 | | `public void insert(E e)` | 插入结点驱动方法 | | `public void remove(E e)` | 删除结点驱动方法 | | `public E findMin()` | 查找最小结点驱动方法 | | `public E findMax()` | 查找最大结点驱动方法 | | `public boolean contains(E e)` | 判断是否包含指定元素驱动方法 | | `public void printTree()` | 按中序遍历打印树的驱动方法 | | `public int size()` | 求树的结点个数驱动方法 | | `public int height()` | 求树的高度驱动方法 | | `public void checkBalance()` | 树平衡检查驱动方法 | | `private AvlNode<E> balance(AvlNode<E> t)` | 调整 $t$ 结点处的平衡,并返回 $t$ 。<br />如果 $t$ 失去平衡,根据其失衡的情况,执行如下四种情形之一的旋转调整。<br />左外情形,对 $t$ 执行右单旋转 $rotateRight$<br />左内情形,对 $t$ 执行左右双旋转 $rotateLeftRight$<br />右外情形,对 $t$ 执行左单旋转 $rotateLeft$<br />右内情形,对 $t$ 执行右左双旋转 $rotateRightLeft$ | | `private AvlNode<E> insert(E e, AvlNode<E> t)` | 插入结点<br />与 BST 的不同在于返回时调用 $balance(t)$ ,<br />调整插入 $t$ 后 $t$ 处的平衡,返回 $t$ 。 | | `private AvlNode<E> remove(E e, AvlNode<E> t)` | 删除结点(懒惰删除)<br />与 BST 的不同在于返回时调用 $balance(t)$ ,<br />调整删除 $t$ 后 $t$ 处的平衡,返回 $t$ (新 $t$ )。 | | `private AvlNode<E> findMin(AvlNode<E> t)` | 返回树的最小结点 | | `private AvlNode<E> findMax(AvlNode<E> t)` | 返回树的最大结点 | | `private boolean contains(E e, AvlNode<E> t)` | 判断树中是否有指定元素的结点 | | `private void printTree(AvlNode<E> t)` | 中序遍历打印树 | | `private int height(AvlNode<E> t)` | 返回以 $t$ 为根结点的树的高度 | | `private int size(AvlNode<E> t)` | 递归地遍历所有结点,返回结点总数 | | `private int checkBalance(AvlNode<E> t)` | 检查树是否平衡,不平衡打印“imbalance”,并返回树高度 | | `private AvlNode<E> rotateRight(AvlNode<E> k2)` | 右单旋转 | | `private AvlNode<E> rotateLeft(AvlNode<E> k1)` | 左单旋转 | | `private AvlNode<E> rotateLeftRight(AvlNode<E> k3)` | 左右双旋转 | | `private AvlNode<E> rotateRightLeft(AvlNode<E> k1)` | 右左双旋转 | 以下为 AVL 树结点嵌套类 $AvlNode$ 的架构。 | 类成员/方法 | 描述 | | ------------------------------------------------------------ | ---------------------- | | `public E element` | 字段,本结点元素 | | `public AvlNode<E> left` | 字段,本结点的左子结点 | | `public AvlNode<E> right` | 字段,本结点的右子结点 | | `public int height` | 字段,该结点的高度 | | `public AvlNode(E theElement)` | 构造器 | | `public AvlNode(E element, AvlNode<E> left, AvlNode<E> right)` | 构造器 | <br /> #### 主要方法 ##### insert 插入结点操作由插入驱动方法和具体插入方法完成,与 BST 的插入方法的不同在于,插入后通过 $balance$ 方法,调整 $t$ 处的平衡后通过返回原根。由于递归,$balance$ 方法能够自底向上调整 **插入路径上所有结点的平衡** ,且实际上在调整 **第一个**(自底向上方向上的第一个)失衡结点后使整棵树恢复为 AVL 树。$balance$ 方法后续详述。 ```java public void insert(E e) { // 插入结点驱动方法 root = insert(e, root); } private AvlNode<E> insert(E e, AvlNode<E> t){ // 插入结点,返回时沿路检查平衡并调整 if(t == null) return new AvlNode<>(e,null, null); int compareRes = e.compareTo(t.element); if(compareRes < 0) t.left = insert(e, t.left); else if(compareRes > 0) t.right = insert(e, t.right); // 等于时不插入(以该树只能存放不同的元素为前提) return balance(t); // 调整t处的平衡并返回t } ``` <br /> ##### findMin/findMax 与 BST 的对应方法一致。 ```java public E findMin() { // 查找最小结点驱动方法 if(isEmpty()) throw new NoSuchElementException(); return findMin(root).element; } private AvlNode<E> findMin(AvlNode<E> t){ // 返回树的最小结点(递归方式) if(t == null) return null; else if(t.left == null) return t; return findMin(t.left); } public E findMax(){ // 查找最大结点驱动方法 if(isEmpty()) throw new NoSuchElementException(); return findMax(root).element; } private AvlNode<E> findMax(AvlNode<E> t){ // 返回树的最大结点(循环方式) if(t == null) return null; while(t.right != null) t = t.right; return t; } ``` <br /> ##### remove 删除结点操作由删除驱动方法和具体删除方法完成,与 BST 的删除方法的不同在于,删除后通过 $balance$ 方法,调整 $t$ 处的平衡后通过返回原根。由于递归,$balance$ 方法能够自底向上调整 **插入路径上所有结点的平衡** ,且实际上在调整 **第一个**(自底向上方向上的第一个)失衡结点后使整棵树恢复为 AVL 树。$balance$ 方法后续详述。 ```java public void remove(E e) { // 删除结点驱动方法 root = remove(e, root); } private AvlNode<E> remove(E e, AvlNode<E> t){ // 删除结点(懒惰删除),返回时沿路检查平衡并调整 if(t == null) return null; int compareRes = e.compareTo(t.element); if(compareRes < 0) t.left = remove(e, t.left); // 递归地在左侧寻找 else if(compareRes > 0) t.right = remove(e, t.right); // 递归地在右侧寻找 // e等于t.element,分两种情形 else if(t.left != null && t.right != null) { // 情形1:该t的左右子结点均不为null t.element = findMin(t.right).element; // 在右子树中找min t.right = remove(t.element, t.right); // 此时min已是t.element,必为情形2 } else t = (t.left != null) ? t.left : t.right; // 情形2: 1以外的情形 return balance(t); // 调整t处的平衡并返回t } ``` <br /> ##### contains 与 BST 的对应方法一致。 ```java public boolean contains(E e) { // 判断是否包含指定元素驱动方法 return contains(e, root); } private boolean contains(E e, AvlNode<E> t) { if(t == null) return false; int compareRes = e.compareTo(t.element); if(compareRes < 0) return contains(e, t.left); else if(compareRes > 0) return contains(e, t.right); else return true; } ``` <br /> ##### balance 在每一次插入或删除结点后,路径上结点 $t$ 的平衡。判断 $t$ 的左右子树高差是否超过设定的值(`ALLOWED_IMBALANCE = 1`),若超过则分别判断属于左-左、左-右、右-右、右-左中的哪一种情形,调用相应的旋转方法调整即可。该方法返回 $t$ 。 ```java private AvlNode<E> balance(AvlNode<E> t){ // 调整 t 结点处的平衡,并返回 t if(t == null) return null; if(height(t.left) - height(t.right) > ALLOWED_IMBALANCE) { // 失衡,且左高于右 if(height(t.left.left) >= height(t.left.right)){ // 右单旋情形 t = rotateRight(t); } else t = rotateLeftRight(t); // 左右双旋情形 } else if(height(t.right) - height(t.left) > ALLOWED_IMBALANCE){ // 失衡,且右高于左 if(height(t.right.right) >= height(t.right.left)) { // 左单旋情形 t = rotateLeft(t); } else t = rotateRightLeft(t); // 右左双旋情形 } t.height = Math.max(height(t.left), height(t.right)) + 1; // 更新 t 的高度 return t; } ``` <br /> ##### rotateRight 右单旋转,见前述说明。 <br /> ##### rotateLeft 左单旋转,见前述说明。 <br /> ##### rotateLeftRight 左右双旋转,见前述说明。 <br /> ##### rotateRightLeft 右左双旋转,见前述说明。 <br /> ##### checkBalance 检查整棵树是否平衡的方法。由平衡检查驱动方法和具体平衡检查方法完成。具体方法中以递归方式检查,若平衡则返回树高,不平衡则打印 $imbalance$ 并返回树高。 ```java public void checkBalance() { // 树平衡检查驱动方法 checkBalance(root); } private int checkBalance(AvlNode<E> t) { // 检查树是否平衡,不平衡打印“imbalance”,并返回树高度 if(t == null) return -1; int lh = checkBalance(t.left); int rh = checkBalance(t.right); if(Math.abs(height(t.left) - height(t.right)) > 1 || height(t.left) != lh || height(t.right) != rh) { System.out.println("imbalance"); } return height(t); } ``` <br /> #### 类的实现代码 ```java class AvlTree<E extends Comparable<? super E>>{ private AvlNode<E> root; private static final int ALLOWED_IMBALANCE = 1; public AvlTree() {} // 无参构造器 public void makeEmpty() { // 树置空 root = null; } public boolean isEmpty() { // 树判空 return root == null; } public void insert(E e) { // 插入结点驱动方法 root = insert(e, root); } public void remove(E e) { // 删除结点驱动方法 root = remove(e, root); } public E findMin() { // 查找最小结点驱动方法 if(isEmpty()) throw new NoSuchElementException(); return findMin(root).element; } public E findMax(){ // 查找最大结点驱动方法 if(isEmpty()) throw new NoSuchElementException(); return findMax(root).element; } public boolean contains(E e) { // 判断是否包含指定元素驱动方法 return contains(e, root); } public void printTree(){ // 按中序遍历打印树的驱动方法 if(isEmpty()) System.out.println("Empty tree"); else printTree(root); } public int size() { // 求树的结点个数驱动方法 return size(root); } public int height() { // 求树的高度驱动方法 return height(root); } public void checkBalance() { // 树平衡检查驱动方法 checkBalance(root); } private AvlNode<E> balance(AvlNode<E> t){ // 调整 t 结点处的平衡,并返回 t if(t == null) return null; if(height(t.left) - height(t.right) > ALLOWED_IMBALANCE) { // 失衡,且左高于右 if(height(t.left.left) >= height(t.left.right)){ // 右单旋情形 t = rotateRight(t); } else t = rotateLeftRight(t); // 左右双旋情形 } else if(height(t.right) - height(t.left) > ALLOWED_IMBALANCE){ // 失衡,且右高于左 if(height(t.right.right) >= height(t.right.left)) { // 左单旋情形 t = rotateLeft(t); } else t = rotateRightLeft(t); // 右左双旋情形 } t.height = Math.max(height(t.left), height(t.right)) + 1; // 更新 t 的高度 return t; } private AvlNode<E> insert(E e, AvlNode<E> t){ // 插入结点,返回时沿路检查平衡并调整 if(t == null) return new AvlNode<>(e,null, null); int compareRes = e.compareTo(t.element); if(compareRes < 0) t.left = insert(e, t.left); else if(compareRes > 0) t.right = insert(e, t.right); // 等于时不插入(以该树只能存放不同的元素为前提) return balance(t); // 调整t处的平衡并返回t } private AvlNode<E> remove(E e, AvlNode<E> t){ // 删除结点(懒惰删除),返回时沿路检查平衡并调整 if(t == null) return null; int compareRes = e.compareTo(t.element); if(compareRes < 0) t.left = remove(e, t.left); // 递归地在左侧寻找 else if(compareRes > 0) t.right = remove(e, t.right); // 递归地在右侧寻找 // e等于t.element,分两种情形 else if(t.left != null && t.right != null) { // 情形1:该t的左右子结点均不为null t.element = findMin(t.right).element; // 在右子树中找min t.right = remove(t.element, t.right); // 此时min已是t.element,必为情形2 } else t = (t.left != null) ? t.left : t.right; // 情形2: 1以外的情形 return balance(t); // 调整t处的平衡并返回t } private AvlNode<E> findMin(AvlNode<E> t){ // 返回树的最小结点(递归方式) if(t == null) return null; else if(t.left == null) return t; return findMin(t.left); } private AvlNode<E> findMax(AvlNode<E> t){ // 返回树的最大结点(循环方式) if(t == null) return null; while(t.right != null) t = t.right; return t; } private boolean contains(E e, AvlNode<E> t) { // 判断树中是否有指定元素的结点 if(t == null) return false; int compareRes = e.compareTo(t.element); if(compareRes < 0) return contains(e, t.left); else if(compareRes > 0) return contains(e, t.right); else return true; } private void printTree(AvlNode<E> t) { // 中序遍历打印树 if(t != null) { printTree(t.left); System.out.println(t.element); printTree(t.right); } } private int height(AvlNode<E> t) { // 返回以t为根结点的树的高度 return t == null ? -1 : t.height; } private int size(AvlNode<E> t) { // 递归地遍历所有结点,返回结点总数 if(t != null) { if(t.left != null && t.right != null) { return 1 + size(t.left) + size(t.right); } else { return t.left != null ? 1 + size(t.left) : 1 + size(t.right); } } return 0; } private int checkBalance(AvlNode<E> t) { // 检查树是否平衡,不平衡打印“imbalance”,并返回树高度 if(t == null) return -1; int lh = checkBalance(t.left); int rh = checkBalance(t.right); if(Math.abs(height(t.left) - height(t.right)) > 1 || height(t.left) != lh || height(t.right) != rh) { System.out.println("imbalance"); } return height(t); } private AvlNode<E> rotateRight(AvlNode<E> k2){ // 右单旋 AvlNode<E> k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = Math.max(height(k2.left), height(k2.right)) + 1; // 调整k2高度 k1.height = Math.max(height(k1.left), height(k1.right)) + 1; // 调整k1高度 return k1; // 返回调整后原失衡处结点 } private AvlNode<E> rotateLeft(AvlNode<E> k1){ // 左单旋 AvlNode<E> k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = Math.max(height(k1.left), height(k1.right)) + 1; // 调整k1高度 k2.height = Math.max(height(k2.left), height(k2.right)) + 1; // 调整k2高度 return k2; // 返回调整后原失衡处结点 } private AvlNode<E> rotateLeftRight(AvlNode<E> k3){ // 左右双旋 k3.left = rotateLeft(k3.left); return rotateRight(k3); } private AvlNode<E> rotateRightLeft(AvlNode<E> k1){ // 右左双旋 k1.right = rotateRight(k1.right); return rotateLeft(k1); } /** * AVL树结点嵌套类 */ private static class AvlNode<E>{ public E element; public AvlNode<E> left, right; // 比BinaryNode多维护一个height字段,每次insert或remove一个结点时通过balance方法更新 public int height; @SuppressWarnings("unused") public AvlNode(E theElement){ this(theElement, null, null); } public AvlNode(E element, AvlNode<E> left, AvlNode<E> right){ this.element = element; this.left = left; this.right = right; this.height = 0; } } } ``` <br /> #### 测试代码 ```java package com.yukiyama; import java.util.NoSuchElementException; public class AvlTreeDemo { public static void main(String[] args) { AvlTree<Integer> t = new AvlTree<>( ); int[] elements = {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9}; for(int e : elements) t.insert(e); t.printTree(); System.out.printf("size: %d, height: %d, min: %d, max: %d\n", t.size(), t.height(), t.findMin(), t.findMax()); // 输出10 System.out.printf("has 10? %s, has 100? %s\n", t.contains(10), t.contains(100)); t.checkBalance(); t.remove(1); t.checkBalance(); t.remove(10); t.checkBalance(); t.remove(16); t.checkBalance(); t.printTree(); // 8 10 13 20 29 74 98 System.out.printf("size: %d, height: %d\n", t.size(), t.height());// 输出0 System.out.println("is empty: " + t.isEmpty()); // false t.makeEmpty(); System.out.println("is empty: " + t.isEmpty()); // true } } ``` <br /> splay树 线段树从入门到急停