Shader中使用距离函数(Distance Function)绘制二维图形 agile Posted on Oct 2 2021 优秀博文 > 本文由 [简悦 SimpRead](http://ksria.com/simpread/) 转码, 原文地址 [zhuanlan.zhihu.com](https://zhuanlan.zhihu.com/p/365440831) 距离函数是什么? -------- 距离函数顾名思义是一个和距离有关的函数,既然是函数,我们就可以用 f(x) 来表示。那么 f(x) 里面干了些什么呢?它会**返回空间中任何一个点到物体表面的最短距离**。 这么说可能有点不好理解,我们来看一个例子,如下图: 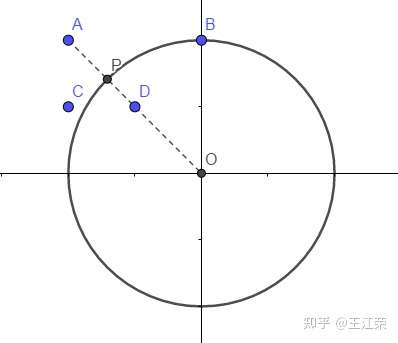 在二维空间中,黑色的圈就是我们圆的物体表面,圆心在原点,半径为 r。而 ABCD 点,是我们空间中任意点的四个采样,我们来看看这些点到圆面上的最短距离 d 怎么算。 通过数学常识我们知道,任意点到圆面的最近距离,必然是该点与圆心的连线在圆上的交点与该点的距离,例如 A 点到圆上的最短距离就是 AP 的长度。PA 的长度自然是 OA 的长度减去 OP 的长度,而 OP 的长度就是半径 r,又因为 O 是原点,因此 OA 的长度就是 A 向量的模,所以 A 点到圆的最短距离即为 |A|-r 。该式子同样适合于其他三个点。 也就是说我们可以得到一个函数 **f(v)=|v|-r** ,输入值 v 即为二维空间中任意点的坐标(一个二维向量),|v | 就是向量 v 的模,代表到原点的长度 / 距离,r 为圆的半径,那个这个函数就是半径为 r,圆心在原点的圆的距离函数。 我们还可以发现,如果 f(x) 的返回值为 0,那么这个点就在圆上,例如 B 点,也就是说我们只要通过这个函数,找出所有返回值为 0 的点,这些点就会形成一个圆。 此外对于 D 点而言,f(x) 返回的是负数,这是因为点在圆内,|D|<r,得到负数,也就是说圆内所有点到圆上的最短距离我们都可以认为是负的。 从圆拓展到所有的几何表面,我们可以总结出,**距离函数会返回空间中任何一个点到物体表面的最短距离,我们只需要找出距离为 0 的所有点,即可得到这个物体表面,而距离小于 0 的点代表在物体内部,距离大于 0 的点代表在物体外**。对于这种带有正负的距离函数,我们也称为**符号距离函数**(Signed Distance Function,简称 SDF)或**定向距离函数**(Oriented Distance Function,简称 SDF)。距离函数在光线追踪中有着重要的作用,我们也可用距离函数来画一些几何体。 附:距离函数 wiki 的解释: [undefined](https://en.wikipedia.org/wiki/Signed_distance_function) 这里大家可能会问,前面的例子我们的圆的圆心正好在原点,所以可以得到 f(v)=|v|-r,那要是不是这样的怎么办?例如下图: 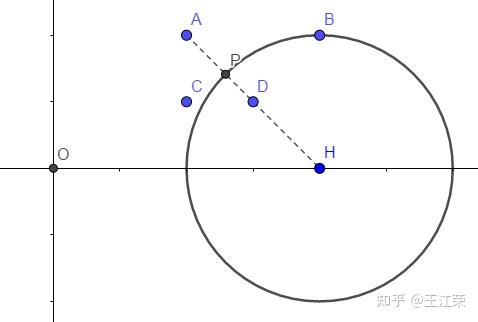 此时 A 到圆心的长度 AH 就不能用 |A| 来代替了,那么我们怎么求 AP 的长度?这里我们可以应用**平移变换**的思想,不管圆心在哪,都是从原点平移了  (设该向量为 h),空间中任意点同样也是平移了 h,把这个平移值去掉就变成了之前的按原点计算,因此对于圆心在 H,半径为 R 的圆,其距离函数为:f(v)=|v-h|-r 。 在 Shader 中使用距离函数绘制二维图形 ---------------------- 既然要用 Shader 绘制,那么就要写 Shader,这里推荐一个网站 [shadertoy](https://www.shadertoy.com/),可以很容易让我们在网站上使用 **GLSL** 语言写一些 Shader。同时里面也有位大神为我们提供了很多二维图形的距离函数: [fractals, computer graphics, mathematics, shaders, demoscene and more](https://www.iquilezles.org/www/articles/distfunctions2d/distfunctions2d.htm) 我们先从最简单的例子来讲起。 有关 Shader 的一些最基础的介绍可以参考 [王江荣:Rendering Pipeline And Shader](https://zhuanlan.zhihu.com/p/364823567) 距离函数画圆 ------ 在前面我们已经说到了圆的距离函数为,f(v)=|v-h|-r,那么在我们代码里,函数就是一段功能代码,我们用 GLSL 来表达的话,如下: ``` float drawCircle(in vec2 p, in vec2 offset, in float r) { return length(p-offset)-r; } ``` 先看输入的值,p 代表任意点的坐标,offset 即圆心和原点的偏移量,r 就是圆的半径。而 length 方法会返回输入的向量的模长。 那么有个问题,offset 和 r 我们很好设置,这个 p 怎么来?空间中任意点,那不就是无数个点了么? 采样空间中的任意点 --------- 对于上面的问题又用到了采样的概念,我们知道屏幕是由像素组成的,且我们的像素只有有一个颜色,而我们能看出物体表面也是因为这些像素显示了物体表面的颜色。那么任意点到物体表面的距离,不就可以简化为任意像素到物体表面的距离,如果距离为 0,那么这个像素就应该显示物体表面的颜色。 也就是说我们只采样所有像素的中心点,带入距离函数即可。并且这个思路在 Shader 中很容易就可以实现,因为我们的 Fragment Shader 就是每个像素调用一次的。 在 GLSL 里,我们的 Fragment Shader 就是下面函数: ``` void mainImage( out vec4 fragColor, in vec2 fragCoord ) { } ``` **fragCoord** 为像素坐标,最终像素的颜色保存在 **fragcolor** 里即可。可参考文档:[https://www.shadertoy.com/howto](https://www.shadertoy.com/howto#q2) 既然 fragCoord 代表的就是像素坐标,那么我们把它带入距离函数不就可以了,代码如下: ``` void mainImage( out vec4 fragColor, in vec2 fragCoord ) { float d = drawCircle(fragCoord, vec2(150.0,50.0), 80.0); vec3 col = vec3(1.0); if(d<-1.0) col = vec3(1.0,0.0,0.0); if(d>1.0) col = vec3(0.0,1.0,0.0); fragColor = vec4(col,1.0); } ``` 注:d 不用 0 来判断是为了让圆有个宽度,否则看不出。此外这些数字后面一定要加 .0 ,否则类型不匹配,编译不过。 得到的效果如下: 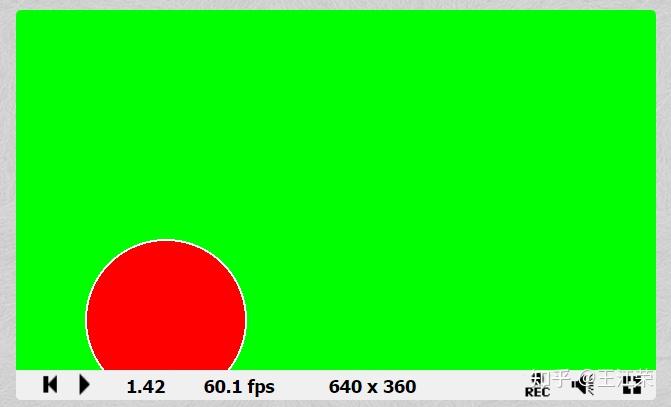 效果是对的,因为屏幕像素是从左下角为原点的。 利用 uv 坐标 -------- 上面的方法有个问题,那就是很难适配不同分辨率的屏幕,屏幕像素越多,这个圆在屏幕内的占比就会越小,如下图: 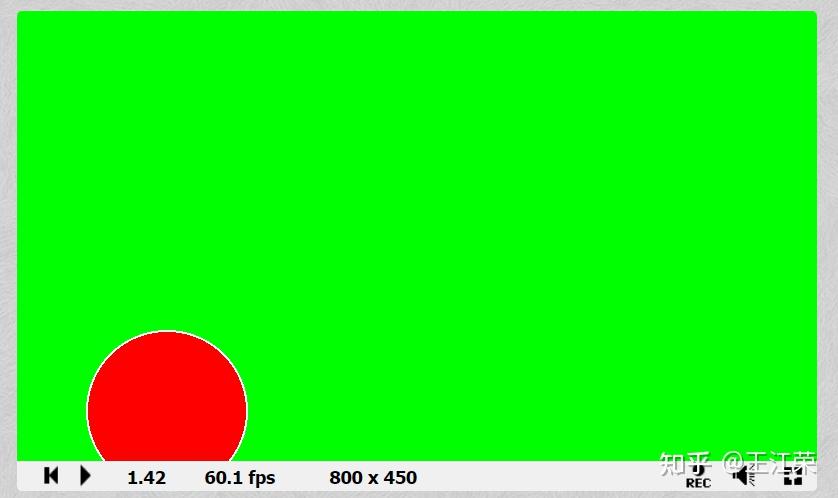 对于这个问题,我们可以用 uv 坐标来解决。 理解起来很简单,本来像素的横坐标是由 0 到 width-1,纵坐标是 0 到 height-1,例如我们像素坐标 (80,80) 就是该像素的真实坐标,它并不会由于 width 和 height 的变换而变换。但是如果我们使像素的横坐标和纵坐标都是 0 到 1,也就是 uv 坐标,那么像素坐标 (0.4,0.4) 对应的真实坐标就会跟着屏幕大小而改变。 在 GLSL 中,提供了 **iResolution** 字段,可以让我们获取到屏幕的分辨率,那么我们将 fragCoord 除以它就是该像素对应的 uv 坐标(这里看着像是向量的除法运算,实则不是,因为向量没有除法运算,这种写法只是把两个向量的 x 和 y 互相相除),代码如下: ``` void mainImage( out vec4 fragColor, in vec2 fragCoord ) { vec2 p = fragCoord/iResolution.xy; float d = drawCircle(p, vec2(0.3,0.2), 0.3); vec3 col = vec3(1.0); if(d<-0.003) col = vec3(1.0,0.0,0.0); if(d>0.003) col = vec3(0.0,1.0,0.0); fragColor = vec4(col,1.0); } ``` 注:需要注意使用 uv 后,对应的偏移,半径和圆宽度判断都要修改数值。 得到结果如下:  擦!圆怎么扁了?这是因为我们 uv 都是 0 到 1,那么长宽不相等的情况下,uv 取值相等的情况下得到的不就是一个扁的玩意嘛。 改!为了解决扁的问题,我们就要使 uv 的取值比值和分辨率的比值相等,例如分辨率 200*100,v 的取值是 0 到 1 的话,那么我们 u 的取值就应该是 0 到 2。也就是说我们取较短的一边对应 0 到 1,而较长的一边按比例往外扩,代码修改如下: ``` vec2 p = fragCoord/iResolution.xy; if (iResolution.x > iResolution.y) { p.x *= iResolution.x / iResolution.y; } else { p.y *= iResolution.y / iResolution.x; } float d = drawCircle(p, vec2(0.3,0.2), 0.3); ``` 如果我们只考虑横屏情况的话,那么 iResolution.x 肯定大于 iResolution.y,所以可以简化一下,为: ``` vec2 p = fragCoord/iResolution.xy; p.x *= iResolution.x / iResolution.y; float d = drawCircle(p, vec2(0.3,0.2), 0.3); ``` 得到结果就正确了(如下图),并且即是分辨率不同了,比例也不会改变。  在屏幕中心绘制 ------- 上面我们都是以左下角为原点,但是往往更多的情况,我们希望以屏幕的中心作为原点来绘制。其实也很简单,我们只需要把 uv 的取值范围从 0 到 1 变为 - 1 到 1 即可,这样取值为 0 时,代表的就是屏幕的中心点,代码如下: ``` vec2 p = fragCoord/iResolution.xy; p = p*2.0-1.0; p.x *= iResolution.x / iResolution.y; float d = drawCircle(p, vec2(0.3,0.2), 0.3); ``` 得到结果为:  偏移量即从屏幕中心开始计算,同时圆也变小了,因为我们圆的半径没变,但是取值范围增加了一倍,所以就变小了。 同时对于上面那一段代码,我们可以进行简写,简写如下(**非常重要!!!**): ``` vec2 p = (2.0*fragCoord-iResolution.xy)/iResolution.y; ``` 简单推一下: 我们先看 p.x:p.x = fragCoord.x/iResolution.x,又因为 p.x = p.x*2-1,所以 p.x = 2*fragCoord.x/iResolution.x-1 = (2*fragCoord.x-iResolution.x)/iResolution.x,然后又因为 p.x *= iResolution.x / iResolution.y,所以最终得到 **p.x = (2*fragCoord.x-iResolution.x)/iResolution.y**。 再来看看 p.y:同理 x,可得到 **p.y** = 2*fragCoord.y/iResolution.y-1 **= (2*fragCoord.y-iResolution.y)/iResolution.y**。 也就是说 xy 的式子是一样的,所以最终得到上面简写的式子。这也是 shadertoy 里面大神们常用的写法,不钻研下都特么的看不懂。 等高线 --- 如图,图中多了很多颜色较深的圈(注意它们不是黑色,只是颜色比较深而已),任意一个圈上的任意一点,到我们物体表面(也就是例子中的圆)的最短距离都相等,这种线我们就称为等高线。  它是怎么画出来的呢?在最后新增下面代码即可: ``` col *= (0.8 + 0.2*cos(100.0*d)); ``` 因为使用 uv 后我们的 d 取值很小,因此乘以 100 来使 cos 的值变化的更快,而 cos 的值永远都是 0 到 1,也就是说 0.2*cos 的值在 0-0.2 之间波动,那么 0.8+0.2*cos 的值在 0.8-1 之间波动。即随着点到物体表面最短距离的距离变化,颜色的值在 col*0.8 和 col*1 之间变化,最短距离相同则颜色相同,图中暗色的线就是 col*0.8 的结果。又因为 cos 是周期函数,因此就出现了一条条的等高线。 布尔操作 ---- 生活中很多复杂的形状其实都是由一些最基本的形状组合起来的。例如**哑铃**,我们可以看做是两个球和一个圆柱拼接起来的,这种由多个形状组合起来的情况我们称之为**并集**。再例如**吸管**,我们可以当做是一个半价较大的圆柱挖掉一个半径较小的圆柱,这种多个形状相减的情况我们称之为**差集**。再例如放大镜的镜子(**透镜**),我们可以认为是两个玻璃球所相交的那部分,这种多个形状只取相交部分的情况我们称之为**交集**。 上述的种种操作都可以使我理由最基础的一些形状组合成更多花里胡哨的形状,而这些操作,我们就称之为几何的布尔操作。 利用距离函数同样可以帮助我们实现几何的布尔操作。 并集(Union,  )/blend ------------------------------------------------------------------- 我们先从最简单的并集来看,前面我们可以通过距离函数画一个圆,那要是我们想要画两个圆怎么办?并且这两个圆可以相交、相切或相离。 我们先用示意图看下两个圆相交的情况:  通过前面的介绍,我们可以用距离函数很轻松的画出圆 O1 或者圆 O2,但是要怎么两个圆都画出来呢(两个圆组成的图案我们就简单称之为结合体吧)? 我们最容易想到的就是根据 O1 和 O2 **把距离函数调用两遍**,但是两遍会得到两个不同的距离,我们应该以哪个距离为准呢? 遇事不决就举例,我们看看几个举例点的情况(设任意某点到圆 O1 的距离为 d1,到圆 O2 的距离为 d2): * 结合体外任意点:例如 A 点,此时 d1>d2,因此到结合体的最短距离应该为 d2。我们可以很容易推理出在结合体外的任意一点到结合体的最短距离应该为 min(d1,d2) 。 * 结合体内任意点:例如 B 点和 C 点,这里要分两种情况,即 KO1LO2 区域内外。为什么?因为该区域外,例如 C 点,d1>0,d2<0,其最短距离依旧是 min(d1,d2) 。但是在该区域内,例如 B 点,虽然还是 d1>0,d2<0,但是其**最短距离是 BK 而不是 d2**。因为 d2 是 B 点到圆 O2 虚线部分一点的距离,而**虚线这部分不再是结合体的表面了**。 * 结合体表面上任意点:例如 D 点,此时 d1>0,d2=0,因为在表面上,最短距离肯定为 0,同样也很容易推理出结合体表面上的任意一点到结合体的最短距离应该为 min(d1,d2) 。 也就是说大部分情况下我们任意点到结合体的距离应该是 **d = min(d1,d2)** ,但是在 KO1LO2 区域内的点却不是,那么我们能不能用 d = min(d1,d2) 代替呢? 如果只是画物体表面,那么答案是可以的。因为我们如果要画物体的表面,那么**只需要找到 d=0 的那些点即可**,而在物体表面内或外的点的最短距离到底是多少,who care,反正不是 0 就行。同时由于 KO1LO2 区域内,使用 d = min(d1,d2) 永远不会导致 d=0,也就是说不会造成该区域内的某些点变成物体表面了。当然了,使用这种方式会造成该区域内的等高线不对,不过一般实际情况下并用不到它。 那么我们就可以用代码来实现了,非常的简单: ``` float drawCircle(in vec2 p, in vec2 offset,in float r) { return length(p-offset)-r; } float opUnion( float d1, float d2 ) { return min(d1,d2); } void mainImage( out vec4 fragColor, in vec2 fragCoord ) { vec2 p = (2.0*fragCoord-iResolution.xy)/iResolution.y; float d1 = drawCircle(p,vec2(0.0,0.7*sin(iTime)), 0.3); float d2 = drawCircle(p, vec2(0.0),0.3); float d = opUnion(d1,d2); vec3 col = vec3(1.0); if(d<-0.005) col = vec3(1.0,0.0,0.0); if(d>0.005) col = vec3(0.0,1.0,0.0); fragColor = vec4(col,1.0); } ``` 注:iTime 代表的是时间,单位为秒,使用 sin(iTime) 就可以随着时间周期变化了。 得到的效果如下:  注:至于两圆相切或相离的情况依旧可以使用 min(d1,d2) 的原因就不多 BB 了,画画图很好理解。 结论:**任意两个几何 A 和 B 并集得到的几何 C,空间中任意点 p 到 C 的最短距离是该点到 A 的最短距离和 B 的最短距离的最小值,即:sdfC(p) = min(sdfA(p), sdfB(p))。** **并集的操作我们也可称为几何的混合(blend)。** 交集(Intersection,  ) -------------------------------------------------------------------- 交集的情况如下,实线部分是结合体表面:  大致的理解和并集差不多,这里就简单写一下: * 结合体外任意点,例如 A,此时 d1>d2,我们应该使用 d1 的值,这里同样存在真实的最短距离应该是 AK 的值,但是我们不管(原因上面解释了)。拓展开来,结合体外任意点的最短距离应该是 max(d1,d2) 。 * 结合体上任意点,例如 C,此时 d1=0,d2<0,因为在结合体表面上,所以去 d1 的值。拓展开来,结合体表面上任意点的最短距离也是 max(d1,d2) 。 * 结合体内任意点,例如 B,此时看着 d2<d1<0,我们应该使用 d1 的值。拓展开来,结合体内任意点的最短距离还是 max(d1,d2) 。 那么我们只需要新增一个取 max 的函数即可,然后调用它: ``` float opIntersection( float d1, float d2 ) { return max(d1,d2); } ``` 效果如下: 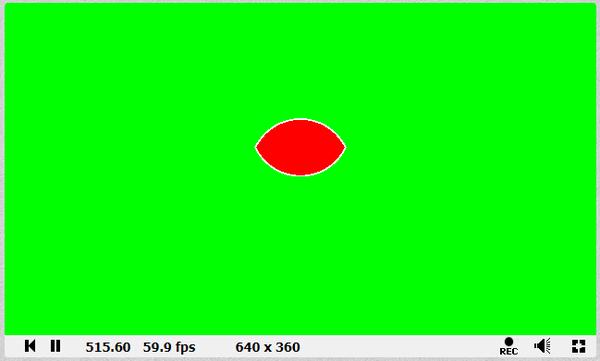 结论:**任意两个几何 A 和 B 交集得到的几何 C,空间中任意点 p 到 C 的最短距离是该点到 A 的最短距离和 B 的最短距离的最大值,即:sdfC(p) = max(sdfA(p), sdfB(p))。** 差集(Subtraction,A\B) ------------------- 差集的示意图如下,O1\O2 即在 O1 上去掉 O2 覆盖的部分:  这里我们换个思路,既然我们只要保证表面上的点的最短距离为 0,其他的点即使距离不对但是只要不等于 0 就行,那么我们直接先看表面上的点来推导好了: * KCL 弧线上的点,例如 C 点,此时 d1<0,d2=0,我们应该取 d2 的值,即 max(d1,d2) 。 * KDL 弧线上的点,例如 D 点,此时 d1=0,d2>0,我们应该取 d1 的值,即 min(d1,d2) 。 我日,一个 max 一个 min?没事,我们可以修改一下对于第二种情况的 min(d1,d2),它不就等价于 max(d1,-d2) 么?且 max(d1,-d2) 也适用于第一种情况。或者是把它们改为 min(-d1,d2) 。 接下来我们要验证 max(d1,-d2) 或者 min(-d1,d2) 会不会在其他情况下也会等于 0,要可能出现等于 0,起码 d1 或者 d2 等于 0,也就是说只可能出现在 KAL 和 KBL 虚线弧上。 * KAL 弧线上的点,例如 A 点,此时 d1>0,d2=0,max(d1,-d2) 不等于 0 ,min(-d1,d2) 不等于 0 。 * KBL 弧线上的点,例如 B 点,此时 d1=0,d2<0,max(d1,-d2) 不等于 0 ,min(-d1,d2) 等于 0 ,枪毙! 结论:**任意两个几何 A 和 B 差集得到的几何 C**,空间中任意点 p 到 C 的最短距离是该点到 A 的最短距离和 B 的最短距离的取反的最大值,即:**sdfC(p) = max(sdfA(p), -sdfB(p)) 。** **注:如果 B\A,那么 sdfB 前面的负号送给 sdfA 即可。** 同样新增一个函数即可: ``` float opSubtraction( float d1, float d2 ) { return max(d1,-d2); } ``` 效果如下: 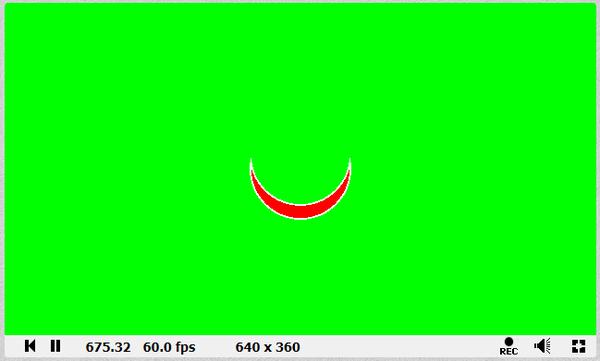 平滑的布尔操作 ------- 前面我们虽然实现了几何之间的布尔操作,但是会发现在交界处**不连续**,例如两个球的并集。而在生活中,这些交界处往往会有道光滑的曲线,例如两滴水滴结合到一起。我们同样可以用代码来解决这个问题,在大神的 [3d 距离函数](https://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm)的文章里的后半部分为我们提供了平滑的布尔操作,分别如下: ``` float opSmoothUnion( float d1, float d2, float k ) { float h = clamp( 0.5 + 0.5*(d2-d1)/k, 0.0, 1.0 ); return mix( d2, d1, h ) - k*h*(1.0-h); } float opSmoothSubtraction( float d1, float d2, float k ) { float h = clamp( 0.5 - 0.5*(d2+d1)/k, 0.0, 1.0 ); return mix( d2, -d1, h ) + k*h*(1.0-h); } float opSmoothIntersection( float d1, float d2, float k ) { float h = clamp( 0.5 - 0.5*(d2-d1)/k, 0.0, 1.0 ); return mix( d2, d1, h ) + k*h*(1.0-h); } ``` 我们来看下 opSmoothUnion 的效果: ``` float d = opSmoothUnion(d1,d2,0.1); ```  我擦,卧戳,我艹,牛逼!!!!!!!!!!!!!!!!!!!!!! 我们先来看里面用到的两个函数的作用: * **clamp(x, min, max)**:返回 x,min 和 max 三个值大小居中的那个,其中参数 min 必须要小于 max。 * **mix(x, y, k)**:返回[线性插值](https://zhuanlan.zhihu.com/p/361943207)的值,即 return (1−k)*x+k*y; 尝试理解下 opSmoothUnion 的原理: 首先第一行 > float h =clamp(0.5+0.5*(d2-d1)/k,0.0,1.0); d2-d1 自然有如下三种情况: * d2-d1>0:这些点分布在下图红色区域,这种情况下,我们 h 的取值范围在 0.5-1 之间,且越接近 KL 直线,h 越接近 0.5,越远离越接近 1 。 * d2-d1<0:这些点分布在下图绿色区域,这种情况下,我们 h 的取值范围在 0.5-0 之间,且越接近 KL 直线,h 越接近 0.5,越远离越接近 0 。 * d2-d1=0:这些点分布在 KL 直线上,h=0.5 。 同时也可发现系数 k 的值越大,h 的变化就越缓慢。 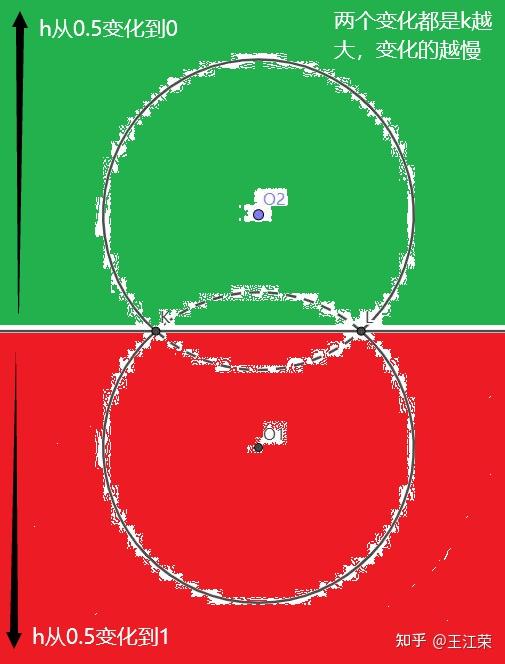 接着是第二行的第一部分: > mix(d2, d1, h) 这里非常的巧妙,当 d2>d1 时,0.5<h<1,mix 的值随着 h 的变化接近 d1,而此时 d1=min(d1,d2)。当 d2<d1 时,0<h<0.5,mix 的值随着 h 的变化接近 d2,而此时 d2=min(d1,d2)。也就是说远离 KL 直线的点到结合体的最短距离就是求了个 min(d1,d2),也就是之前的 opUnion 操作。因此使用 opUnion 或使用 opSmoothUnion,在远离 KL 直线处,得到的表面时一样的。除非你 k 设的比较大,那样表面会变大,因为当 k 很大时,h 接近 1 或者 0 的速度变慢,使得 mix( d2, d1, h ) > min(d1,d2),导致球变小。 而接近 KL 直线的地方,mix(d2, d1, h) 必然大于 min(d1,d2),会导致这部分表面向里面压缩。又因为当 d1 和 d2 越接近,mix( d2, d1, h ) 越接近 min(d1,d2),因此会变成向内凹的弧线。 会得到如下的结果:  如果增加 k 的值,会得到:  很明显可以看出,如果只用 mix,效果依旧不好,因此我们再来看看第二行的第二部分: > k*h*(1.0-h); 注:我们设这部分得到的值为 x 。 我们先来看下 k*h*(1-h) ,0<=h<=1 的函数曲线,如下图,k 的值越大,曲线会越抖。 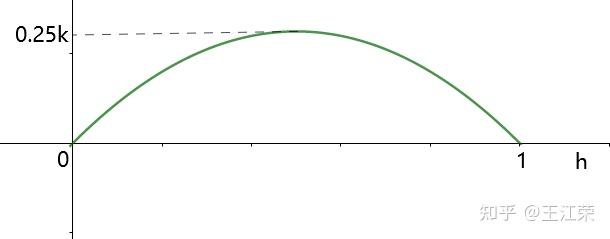 首先当 h=1 或者 h=0 时,x=0,即不影响远离 KL 直线处的表面。但是此时当 k 偏大时,会使得 mix(d2, d1, h) - x < min(d1,d2),所以 k 偏大时,球会变大。 当 0<h<1 时,也就是靠近 KL 直线的表面,会被减去 x 的值,即表面向外扩展。且越靠近 KL 直线,向外扩的越越多,使得之前的内凹曲线更加平滑。 得到结果如下:  若 k 值偏大,得到结果为: 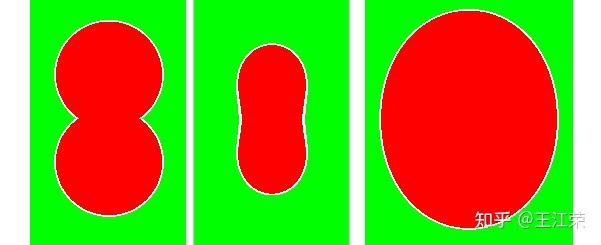 其他平滑效果的原理类似。 其他的二维图形 ------- 其他的一些基本二维图形在前面给的大神文章里面基本都有介绍到,这里也就不过多的比比了。 大家也可以参考下面这篇文章 [undefined](https://blog.csdn.net/qq_41368247/article/details/106194092) 使用 Unity 的 Shader 代替 -------------------- 由于 Shadertoy 需要翻墙,或者说网页里那些牛逼的效果我们想要用到 Unity 里,由于 Unity 是 HLSL 写的,因此我们需要把 GLSL 语言转换一下。在 HLSL 官方文档里介绍到了一些转换: [undefined](https://docs.microsoft.com/zh-cn/windows/uwp/gaming/glsl-to-hlsl-reference) 例如: <table data-draft-node="block" data-draft-type="table" data-size="normal" data-row-style="normal"><tbody><tr><td>GLSL</td><td>HLSL</td></tr><tr><td>iResolution</td><td>_ScreenParams</td></tr><tr><td>vec2</td><td>float2/fixed2</td></tr><tr><td>片段着色器:void mainImage(out vec4 fragColor, in vec2 fragCoord)</td><td>像素着色器:fixed4 frag (v2f i) : SV_Target</td></tr><tr><td>mix()</td><td>lerp()</td></tr><tr><td>屏幕坐标左下角为原点</td><td>屏幕坐标左上角为原点</td></tr></tbody></table> 我们这里简单的把前面绘制圆的 GLSL 代码转一下,如下: ``` Shader "Unlit/NewUnlitShader" { Properties { } SubShader { Tags { "RenderType"="Opaque" } LOD 100 Pass { CGPROGRAM #pragma vertex vert #pragma fragment frag #include "UnityCG.cginc" struct appdata { float4 vertex : POSITION; }; struct v2f { float4 pos:POSITION; }; v2f vert (appdata v) { v2f o; //将顶点坐标由对象空间转到屏幕空间 o.pos = UnityObjectToClipPos(v.vertex); return o; } float drawCircle(in fixed2 p, in fixed2 offset, in float r) { return length(p-offset)-r; } fixed4 frag (v2f i) : SV_Target { //变为左下角为原点 i.pos.y = _ScreenParams.y - i.pos.y; //插值得到的i.pos等价于fragCoord fixed2 p = (2.0 * i.pos - _ScreenParams.xy) / _ScreenParams.y; float d = drawCircle(p, fixed2(0.0,0.0), 0.5); fixed3 col = fixed3(1.0,1.0,1.0); if(d<-0.003) col = fixed3(1.0,0.0,0.0); if(d>0.003) col = fixed3(0.0,1.0,0.0); col *= (0.8 + 0.2*cos(100.0*d)); return fixed4(col,1.0); } ENDCG } } } ``` 然后我们用 UGUI 建个 Image,拖上带有这个 Shader 的 Material 即可。 画圆角(Round Operate) ------------------ 我们先来看一个长方形的距离函数: ``` float drawBox( in vec2 p, in vec2 b ) { vec2 d = abs(p)-b; return length(max(d,0.0)) + min(max(d.x,d.y),0.0); } ``` 它得到的效果如下(截图效果是前面链接里大佬做的效果,我就直接盗用劳动成果了~): ``` float d = drawBox(p,vec2(0.4,0.3)); ``` 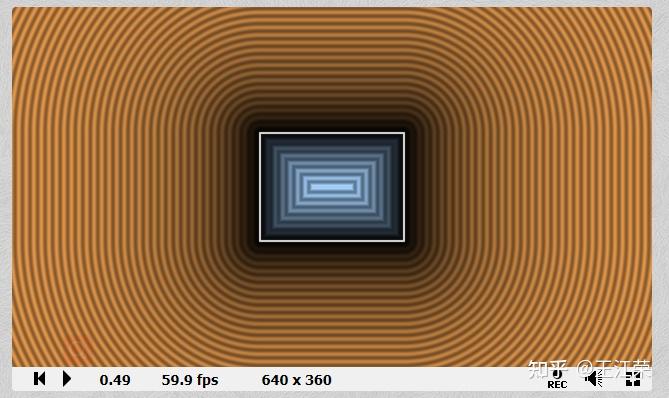 此时长方形的的四个角都是直角,然后现在的审美都流行锐角的图案,例如 app 的 icon,小米公司新版的 logo 啊。那么我们怎么修改能得到一个锐角的长方形呢? 非常的简单,我们**设我们的距离函数为 d = sdf(p),我们只需要改为 d = sdf(p)-r 即可,r 为锐角半径**。 我们举个三角形的例子来理解下: 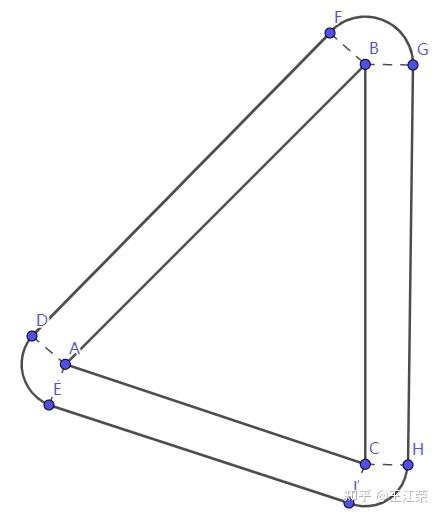 我们用 d=sdf(p) 绘制出三角形 ABC,此时 sdf(A)=0。当改为 d=sdf(p)-r 时,sdf(A)-r=-r,也就是说我们此时 A 点在新的表面内部,且离新表面的最短距离为 r,也就是说我们原本三角形 ABC 的表面会**向外扩 r 的长度**。那么线段 AB 就会变为线段 DF,BC 变 GH,AC 变 EI,但是这三条线段并不能变成一个完整的三角形,在三个顶点处会有**缺口**。而在这些缺口出要找到离三角形 ABC 最短距离为 r 的点,自然是在 ABC 三个顶点半价为 r 的圆弧上。因此 d=sdf(p)-r 就会得到外面这个圆角的三角形。 对于其他的直角图形也是同理,就比如前面的长方形,其实在长方形外面的等高线就可以看出端倪了,外面的那些等高线并不是直角的。三角形内部等高线是直角的,至于原因简单想想肯定能想通。  那么我们就可以新增一个函数,用于实现 sdf(p)-r,对于前面的长方形而言,该函数如下: ``` float opRound( in vec2 p, in float r ) { return drawBox(p, vec2(0.4,0.3)) - r; } ``` 然后调用它即可 ``` float d = opRound(p,0.1); ``` 得到的效果为: 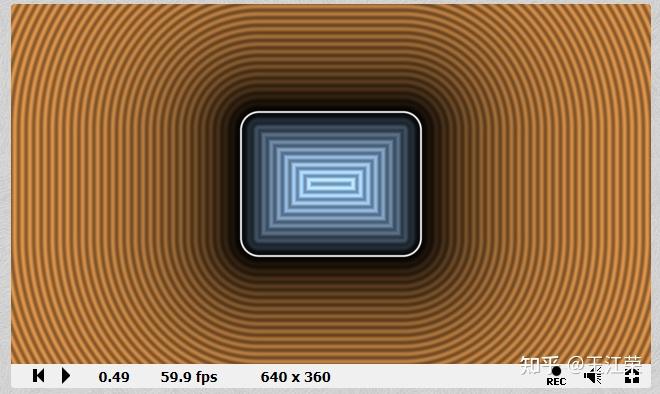 画环状(Annular Operate) -------------------- 同样我们还可以用距离还是画环装图形,不多废话了,只需要**把 d = sdf(p),改为 d = |sdf(p)|-r 即可,r 为环宽的一半**。 我们还是用三角形举例子:  使用 d = sdf(p) 可以得到三角形 ABC,而 d = |sdf(p)|-r 即把原本的距离函数返回的距离取绝对值,那么我们来看看正负两种情况。 * 正,即 sdf(p) > 0,点在三角形外,那么等价于 d = sdf(p)-r 。这不就是我们上面所说的画圆角的情况,即可得到上图中最外一圈的形状。 * 负,即 sdf(p) < 0,点在三角形内,当 -r < sdf(p) < 0 时,|sdf(p)|-r<0,即点在新的图形内。当 sdf(p) = -r 时,|sdf(p)|-r=0,即点在新图形表面上。当 sdf(p) < -r 时,|sdf(p)|-r>0,即点在新图形外。也就是说三角形 ABC 向内缩了 r 长度变成了 JKL,且内外相反了。 两者结合,即上图中最外圈与最内圈结合,可以得到一个环状的图形。 代码用之前长方形做例子: ``` float opAnnular( in vec2 p, in float r ) { return abs(drawBox(p,vec2(0.4,0.3))) - r; } ``` 调用: ``` float d = opAnnular(p, 0.1); ``` 得到的效果为:  用距离函数绘制三维图形 ----------- [fractals, computer graphics, mathematics, shaders, demoscene and more](https://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm) 在大神的这篇文章里,介绍了三维几何的距离函数,但是当我点第一个进去的时候,就蒙蔽了  这搞毛呀,其实想想也是,大家都是显示在二维平面上的一个圈,为毛你是圆我是球,无非就是着色给人带来的感觉,而着色又要和光照相关联。 除了三维几何的距离函数外,该文章后面还介绍了很多的几何操作,例如前面提到的布尔操作,环状,圆角,还有还未看明白的扭曲,变形,重复等操作。 因此想要真正自己用距离函数绘制出三维的几何,还需要很多的学习。等我学会了再说~ 简单例子: [王江荣:使用距离函数绘制 3D 几何](https://zhuanlan.zhihu.com/p/367712078) Unity里的Procedural Animation 使用Raymarching和DistanceFunction绘制3D几何